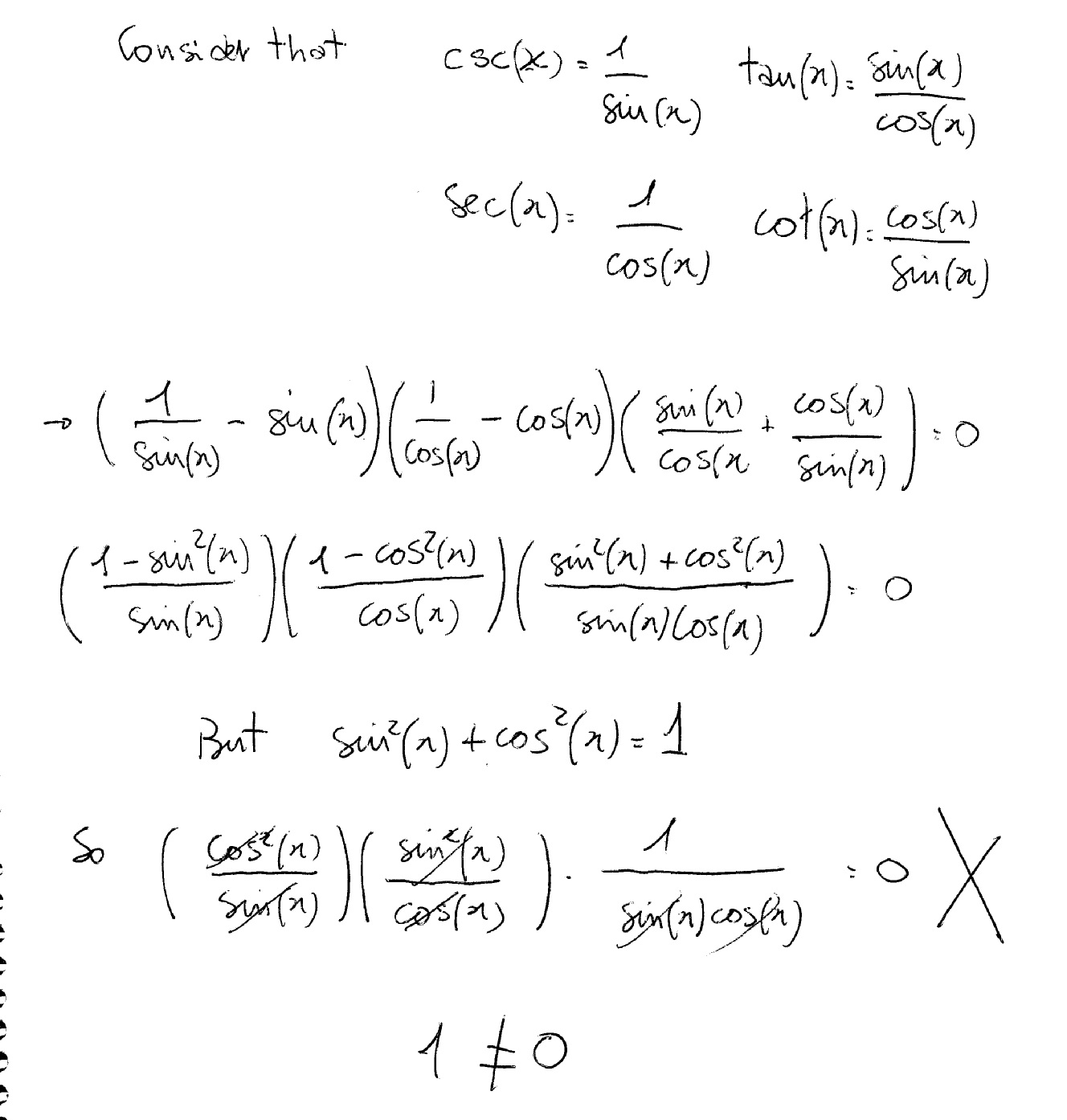Cot X Sec X Cos X . Divide the fundamental identity sin^2x + cos^2x = 1 by sin^2x or cos^2x to derive the other two: The remaining trigonometric functions secant (sec), cosecant (csc), and cotangent (cot) are defined as the reciprocal functions of cosine, sine, and tangent, respectively. In mathematics, an identity is an equation which is always true, regardless of the specific value of a given variable. Trigonometric identities calculator online with solution and steps. Detailed step by step solutions to your trigonometric identities problems with. We can interpret the cotangent of a negative angle as cot(− θ) = cos (− θ) sin (− θ) = cosθ − sin θ = − cot θ. An identity can be trivially. 1 + cot^2x = csc^2x. The points labeled 1, sec(θ), csc(θ) represent the length of the line segment from the origin to that point. Sin^2x/sin^2x + cos^2x/sin^2x = 1/sin^2x.
from socratic.org
The points labeled 1, sec(θ), csc(θ) represent the length of the line segment from the origin to that point. An identity can be trivially. The remaining trigonometric functions secant (sec), cosecant (csc), and cotangent (cot) are defined as the reciprocal functions of cosine, sine, and tangent, respectively. Trigonometric identities calculator online with solution and steps. 1 + cot^2x = csc^2x. In mathematics, an identity is an equation which is always true, regardless of the specific value of a given variable. Divide the fundamental identity sin^2x + cos^2x = 1 by sin^2x or cos^2x to derive the other two: Detailed step by step solutions to your trigonometric identities problems with. We can interpret the cotangent of a negative angle as cot(− θ) = cos (− θ) sin (− θ) = cosθ − sin θ = − cot θ. Sin^2x/sin^2x + cos^2x/sin^2x = 1/sin^2x.
How do you verify the identity (csc x sin x)(sec x cos x)(tan x
Cot X Sec X Cos X An identity can be trivially. The remaining trigonometric functions secant (sec), cosecant (csc), and cotangent (cot) are defined as the reciprocal functions of cosine, sine, and tangent, respectively. Divide the fundamental identity sin^2x + cos^2x = 1 by sin^2x or cos^2x to derive the other two: Detailed step by step solutions to your trigonometric identities problems with. Sin^2x/sin^2x + cos^2x/sin^2x = 1/sin^2x. In mathematics, an identity is an equation which is always true, regardless of the specific value of a given variable. The points labeled 1, sec(θ), csc(θ) represent the length of the line segment from the origin to that point. 1 + cot^2x = csc^2x. Trigonometric identities calculator online with solution and steps. We can interpret the cotangent of a negative angle as cot(− θ) = cos (− θ) sin (− θ) = cosθ − sin θ = − cot θ. An identity can be trivially.
From www.numerade.com
SOLVED Simplify. cot(x) csc(x) cos(x) Use algebra and the fundamental Cot X Sec X Cos X Trigonometric identities calculator online with solution and steps. We can interpret the cotangent of a negative angle as cot(− θ) = cos (− θ) sin (− θ) = cosθ − sin θ = − cot θ. Sin^2x/sin^2x + cos^2x/sin^2x = 1/sin^2x. The remaining trigonometric functions secant (sec), cosecant (csc), and cotangent (cot) are defined as the reciprocal functions of cosine,. Cot X Sec X Cos X.
From www.youtube.com
17 Reciprocal functions sec, cosec and cot YouTube Cot X Sec X Cos X Divide the fundamental identity sin^2x + cos^2x = 1 by sin^2x or cos^2x to derive the other two: In mathematics, an identity is an equation which is always true, regardless of the specific value of a given variable. Detailed step by step solutions to your trigonometric identities problems with. An identity can be trivially. 1 + cot^2x = csc^2x. The. Cot X Sec X Cos X.
From www.chegg.com
Solved Verify the identity. Cot X Sec X Cos X 1 + cot^2x = csc^2x. Sin^2x/sin^2x + cos^2x/sin^2x = 1/sin^2x. The points labeled 1, sec(θ), csc(θ) represent the length of the line segment from the origin to that point. An identity can be trivially. In mathematics, an identity is an equation which is always true, regardless of the specific value of a given variable. Detailed step by step solutions to. Cot X Sec X Cos X.
From www.numerade.com
SOLVED Verify the Identity by converting the left side into sines and Cot X Sec X Cos X Trigonometric identities calculator online with solution and steps. Divide the fundamental identity sin^2x + cos^2x = 1 by sin^2x or cos^2x to derive the other two: The remaining trigonometric functions secant (sec), cosecant (csc), and cotangent (cot) are defined as the reciprocal functions of cosine, sine, and tangent, respectively. We can interpret the cotangent of a negative angle as cot(−. Cot X Sec X Cos X.
From socratic.org
How do you verify the identity (csc x sin x)(sec x cos x)(tan x Cot X Sec X Cos X Trigonometric identities calculator online with solution and steps. Divide the fundamental identity sin^2x + cos^2x = 1 by sin^2x or cos^2x to derive the other two: Detailed step by step solutions to your trigonometric identities problems with. 1 + cot^2x = csc^2x. The points labeled 1, sec(θ), csc(θ) represent the length of the line segment from the origin to that. Cot X Sec X Cos X.
From brainly.lat
Sen x Cos x Tan x Cot x Sec x Brainly.lat Cot X Sec X Cos X Sin^2x/sin^2x + cos^2x/sin^2x = 1/sin^2x. Trigonometric identities calculator online with solution and steps. 1 + cot^2x = csc^2x. The remaining trigonometric functions secant (sec), cosecant (csc), and cotangent (cot) are defined as the reciprocal functions of cosine, sine, and tangent, respectively. The points labeled 1, sec(θ), csc(θ) represent the length of the line segment from the origin to that point.. Cot X Sec X Cos X.
From www.gauthmath.com
Solved sin x/cot x =sec xcos x [Calculus] Cot X Sec X Cos X We can interpret the cotangent of a negative angle as cot(− θ) = cos (− θ) sin (− θ) = cosθ − sin θ = − cot θ. The points labeled 1, sec(θ), csc(θ) represent the length of the line segment from the origin to that point. Trigonometric identities calculator online with solution and steps. Sin^2x/sin^2x + cos^2x/sin^2x = 1/sin^2x.. Cot X Sec X Cos X.
From www.youtube.com
sen x/cos x + tan x/cot x + sec x/csc x=2cot x+1/cot2 x YouTube Cot X Sec X Cos X The points labeled 1, sec(θ), csc(θ) represent the length of the line segment from the origin to that point. We can interpret the cotangent of a negative angle as cot(− θ) = cos (− θ) sin (− θ) = cosθ − sin θ = − cot θ. 1 + cot^2x = csc^2x. Detailed step by step solutions to your trigonometric. Cot X Sec X Cos X.
From www.numerade.com
SOLVED For the following exercises, simplify the first trigonometric Cot X Sec X Cos X We can interpret the cotangent of a negative angle as cot(− θ) = cos (− θ) sin (− θ) = cosθ − sin θ = − cot θ. 1 + cot^2x = csc^2x. Trigonometric identities calculator online with solution and steps. The remaining trigonometric functions secant (sec), cosecant (csc), and cotangent (cot) are defined as the reciprocal functions of cosine,. Cot X Sec X Cos X.
From www.youtube.com
Buktikan cot x = (sec x. Cos x) /tan x YouTube Cot X Sec X Cos X The remaining trigonometric functions secant (sec), cosecant (csc), and cotangent (cot) are defined as the reciprocal functions of cosine, sine, and tangent, respectively. 1 + cot^2x = csc^2x. We can interpret the cotangent of a negative angle as cot(− θ) = cos (− θ) sin (− θ) = cosθ − sin θ = − cot θ. Divide the fundamental identity. Cot X Sec X Cos X.
From www.chegg.com
Solved 25. Verify the identity. csc(x) cot(x) sec(x) 1 Cot X Sec X Cos X Sin^2x/sin^2x + cos^2x/sin^2x = 1/sin^2x. Detailed step by step solutions to your trigonometric identities problems with. We can interpret the cotangent of a negative angle as cot(− θ) = cos (− θ) sin (− θ) = cosθ − sin θ = − cot θ. Trigonometric identities calculator online with solution and steps. 1 + cot^2x = csc^2x. The remaining trigonometric. Cot X Sec X Cos X.
From kunduz.com
[ANSWERED] Factor and simplify 2 cot x sec x sec x cot x Math Cot X Sec X Cos X 1 + cot^2x = csc^2x. The points labeled 1, sec(θ), csc(θ) represent the length of the line segment from the origin to that point. An identity can be trivially. Trigonometric identities calculator online with solution and steps. In mathematics, an identity is an equation which is always true, regardless of the specific value of a given variable. Sin^2x/sin^2x + cos^2x/sin^2x. Cot X Sec X Cos X.
From www.chegg.com
Solved solve for sin x, cos x, tan x, cot x, sec x, csc x Cot X Sec X Cos X 1 + cot^2x = csc^2x. Trigonometric identities calculator online with solution and steps. The points labeled 1, sec(θ), csc(θ) represent the length of the line segment from the origin to that point. An identity can be trivially. We can interpret the cotangent of a negative angle as cot(− θ) = cos (− θ) sin (− θ) = cosθ − sin. Cot X Sec X Cos X.
From www.chegg.com
Solved Multiply and simplify. cos x sin x(cotx + sec x) cos Cot X Sec X Cos X We can interpret the cotangent of a negative angle as cot(− θ) = cos (− θ) sin (− θ) = cosθ − sin θ = − cot θ. Divide the fundamental identity sin^2x + cos^2x = 1 by sin^2x or cos^2x to derive the other two: Detailed step by step solutions to your trigonometric identities problems with. Sin^2x/sin^2x + cos^2x/sin^2x. Cot X Sec X Cos X.
From www.youtube.com
1. Probar que (cos x sec x)/tan x=cot x YouTube Cot X Sec X Cos X Trigonometric identities calculator online with solution and steps. We can interpret the cotangent of a negative angle as cot(− θ) = cos (− θ) sin (− θ) = cosθ − sin θ = − cot θ. An identity can be trivially. In mathematics, an identity is an equation which is always true, regardless of the specific value of a given. Cot X Sec X Cos X.
From www.numerade.com
SOLVEDSimplify the given expressions. The result will be one of sin x Cot X Sec X Cos X The points labeled 1, sec(θ), csc(θ) represent the length of the line segment from the origin to that point. Sin^2x/sin^2x + cos^2x/sin^2x = 1/sin^2x. An identity can be trivially. Trigonometric identities calculator online with solution and steps. In mathematics, an identity is an equation which is always true, regardless of the specific value of a given variable. Divide the fundamental. Cot X Sec X Cos X.
From www.chegg.com
Solved sinx= cosx= tanx= cotx= secx= cscx= Cot X Sec X Cos X Divide the fundamental identity sin^2x + cos^2x = 1 by sin^2x or cos^2x to derive the other two: The points labeled 1, sec(θ), csc(θ) represent the length of the line segment from the origin to that point. An identity can be trivially. 1 + cot^2x = csc^2x. The remaining trigonometric functions secant (sec), cosecant (csc), and cotangent (cot) are defined. Cot X Sec X Cos X.
From abjohn.com
Trigonometry Formulas Knowledge Base ABJOHN Cot X Sec X Cos X In mathematics, an identity is an equation which is always true, regardless of the specific value of a given variable. Divide the fundamental identity sin^2x + cos^2x = 1 by sin^2x or cos^2x to derive the other two: Trigonometric identities calculator online with solution and steps. We can interpret the cotangent of a negative angle as cot(− θ) = cos. Cot X Sec X Cos X.
From www.numerade.com
SOLVED verify the identity. (tan x cot x)/(cos x)=sec x Cot X Sec X Cos X An identity can be trivially. We can interpret the cotangent of a negative angle as cot(− θ) = cos (− θ) sin (− θ) = cosθ − sin θ = − cot θ. In mathematics, an identity is an equation which is always true, regardless of the specific value of a given variable. 1 + cot^2x = csc^2x. Detailed step. Cot X Sec X Cos X.
From www.chegg.com
Solved COS X + 1 + sinx 1 + sinx = 2 sec X COS X csc x(cot Cot X Sec X Cos X The remaining trigonometric functions secant (sec), cosecant (csc), and cotangent (cot) are defined as the reciprocal functions of cosine, sine, and tangent, respectively. We can interpret the cotangent of a negative angle as cot(− θ) = cos (− θ) sin (− θ) = cosθ − sin θ = − cot θ. The points labeled 1, sec(θ), csc(θ) represent the length. Cot X Sec X Cos X.
From www.doubtnut.com
(cotx)/(1+cosec x)+ (1+cosec x)/(cot x) is equal to (cotx)/(1+cosec Cot X Sec X Cos X An identity can be trivially. Detailed step by step solutions to your trigonometric identities problems with. In mathematics, an identity is an equation which is always true, regardless of the specific value of a given variable. The points labeled 1, sec(θ), csc(θ) represent the length of the line segment from the origin to that point. Sin^2x/sin^2x + cos^2x/sin^2x = 1/sin^2x.. Cot X Sec X Cos X.
From www.geogebra.org
The functions cosec x, sec x and cot x GeoGebra Cot X Sec X Cos X The points labeled 1, sec(θ), csc(θ) represent the length of the line segment from the origin to that point. Divide the fundamental identity sin^2x + cos^2x = 1 by sin^2x or cos^2x to derive the other two: Sin^2x/sin^2x + cos^2x/sin^2x = 1/sin^2x. Detailed step by step solutions to your trigonometric identities problems with. An identity can be trivially. The remaining. Cot X Sec X Cos X.
From socratic.org
How do you verify the identity (cot x) / (csc x +1) = (csc x 1 Cot X Sec X Cos X In mathematics, an identity is an equation which is always true, regardless of the specific value of a given variable. The points labeled 1, sec(θ), csc(θ) represent the length of the line segment from the origin to that point. 1 + cot^2x = csc^2x. We can interpret the cotangent of a negative angle as cot(− θ) = cos (− θ). Cot X Sec X Cos X.
From www.numerade.com
SOLVED Simplify the trigonometric expression below by writing the Cot X Sec X Cos X An identity can be trivially. In mathematics, an identity is an equation which is always true, regardless of the specific value of a given variable. Detailed step by step solutions to your trigonometric identities problems with. Trigonometric identities calculator online with solution and steps. 1 + cot^2x = csc^2x. We can interpret the cotangent of a negative angle as cot(−. Cot X Sec X Cos X.
From www.youtube.com
prove that cos^4 x sin^4 x / 1 tan x = (cot x 1) / sec x cosec x Cot X Sec X Cos X An identity can be trivially. Sin^2x/sin^2x + cos^2x/sin^2x = 1/sin^2x. Divide the fundamental identity sin^2x + cos^2x = 1 by sin^2x or cos^2x to derive the other two: The remaining trigonometric functions secant (sec), cosecant (csc), and cotangent (cot) are defined as the reciprocal functions of cosine, sine, and tangent, respectively. The points labeled 1, sec(θ), csc(θ) represent the length. Cot X Sec X Cos X.
From www.youtube.com
Graphs of Sec x, Cosec x and Cot x (Edexcel IAL P3 3.2) YouTube Cot X Sec X Cos X Trigonometric identities calculator online with solution and steps. Sin^2x/sin^2x + cos^2x/sin^2x = 1/sin^2x. Divide the fundamental identity sin^2x + cos^2x = 1 by sin^2x or cos^2x to derive the other two: An identity can be trivially. We can interpret the cotangent of a negative angle as cot(− θ) = cos (− θ) sin (− θ) = cosθ − sin θ. Cot X Sec X Cos X.
From www.youtube.com
Differentiating sec(x), cosec(x) and cot(x) ExamSolutions Maths Cot X Sec X Cos X Trigonometric identities calculator online with solution and steps. Detailed step by step solutions to your trigonometric identities problems with. 1 + cot^2x = csc^2x. We can interpret the cotangent of a negative angle as cot(− θ) = cos (− θ) sin (− θ) = cosθ − sin θ = − cot θ. In mathematics, an identity is an equation which. Cot X Sec X Cos X.
From www.youtube.com
Reciprocal Trigonometric Functions (Cosecant, Secant, Cotangent) YouTube Cot X Sec X Cos X The points labeled 1, sec(θ), csc(θ) represent the length of the line segment from the origin to that point. Sin^2x/sin^2x + cos^2x/sin^2x = 1/sin^2x. Divide the fundamental identity sin^2x + cos^2x = 1 by sin^2x or cos^2x to derive the other two: We can interpret the cotangent of a negative angle as cot(− θ) = cos (− θ) sin (−. Cot X Sec X Cos X.
From www.numerade.com
SOLVED Verify the identity by converting the left side into sines and Cot X Sec X Cos X The remaining trigonometric functions secant (sec), cosecant (csc), and cotangent (cot) are defined as the reciprocal functions of cosine, sine, and tangent, respectively. Divide the fundamental identity sin^2x + cos^2x = 1 by sin^2x or cos^2x to derive the other two: Detailed step by step solutions to your trigonometric identities problems with. Trigonometric identities calculator online with solution and steps.. Cot X Sec X Cos X.
From www.youtube.com
Identidades; a) csc x cos x=cot x; b) sec x sen x=tan x; c) tan x cot x Cot X Sec X Cos X An identity can be trivially. The remaining trigonometric functions secant (sec), cosecant (csc), and cotangent (cot) are defined as the reciprocal functions of cosine, sine, and tangent, respectively. Trigonometric identities calculator online with solution and steps. 1 + cot^2x = csc^2x. Sin^2x/sin^2x + cos^2x/sin^2x = 1/sin^2x. Detailed step by step solutions to your trigonometric identities problems with. The points labeled. Cot X Sec X Cos X.
From www.numerade.com
SOLVEDSimplify the given expressions. The result will be one of sin x Cot X Sec X Cos X The points labeled 1, sec(θ), csc(θ) represent the length of the line segment from the origin to that point. We can interpret the cotangent of a negative angle as cot(− θ) = cos (− θ) sin (− θ) = cosθ − sin θ = − cot θ. Sin^2x/sin^2x + cos^2x/sin^2x = 1/sin^2x. Divide the fundamental identity sin^2x + cos^2x =. Cot X Sec X Cos X.
From www.youtube.com
Verify the Trigonometric Identity (cos^2(x) tan^2(x))/sin^2(x) = cot Cot X Sec X Cos X We can interpret the cotangent of a negative angle as cot(− θ) = cos (− θ) sin (− θ) = cosθ − sin θ = − cot θ. In mathematics, an identity is an equation which is always true, regardless of the specific value of a given variable. Detailed step by step solutions to your trigonometric identities problems with. The. Cot X Sec X Cos X.
From www.numerade.com
Simplify the expression. sinx(tan x K cotx) sec X cOS X CSC X cot X Cot X Sec X Cos X In mathematics, an identity is an equation which is always true, regardless of the specific value of a given variable. We can interpret the cotangent of a negative angle as cot(− θ) = cos (− θ) sin (− θ) = cosθ − sin θ = − cot θ. Divide the fundamental identity sin^2x + cos^2x = 1 by sin^2x or. Cot X Sec X Cos X.
From revisionmaths.com
Sec, Cosec and Cot Mathematics ALevel Revision Cot X Sec X Cos X Trigonometric identities calculator online with solution and steps. Divide the fundamental identity sin^2x + cos^2x = 1 by sin^2x or cos^2x to derive the other two: The remaining trigonometric functions secant (sec), cosecant (csc), and cotangent (cot) are defined as the reciprocal functions of cosine, sine, and tangent, respectively. 1 + cot^2x = csc^2x. Sin^2x/sin^2x + cos^2x/sin^2x = 1/sin^2x. We. Cot X Sec X Cos X.
From www.gauthmath.com
Solved tan x+cot x=sec x· cos ecx [Calculus] Cot X Sec X Cos X Divide the fundamental identity sin^2x + cos^2x = 1 by sin^2x or cos^2x to derive the other two: Sin^2x/sin^2x + cos^2x/sin^2x = 1/sin^2x. The points labeled 1, sec(θ), csc(θ) represent the length of the line segment from the origin to that point. An identity can be trivially. We can interpret the cotangent of a negative angle as cot(− θ) =. Cot X Sec X Cos X.