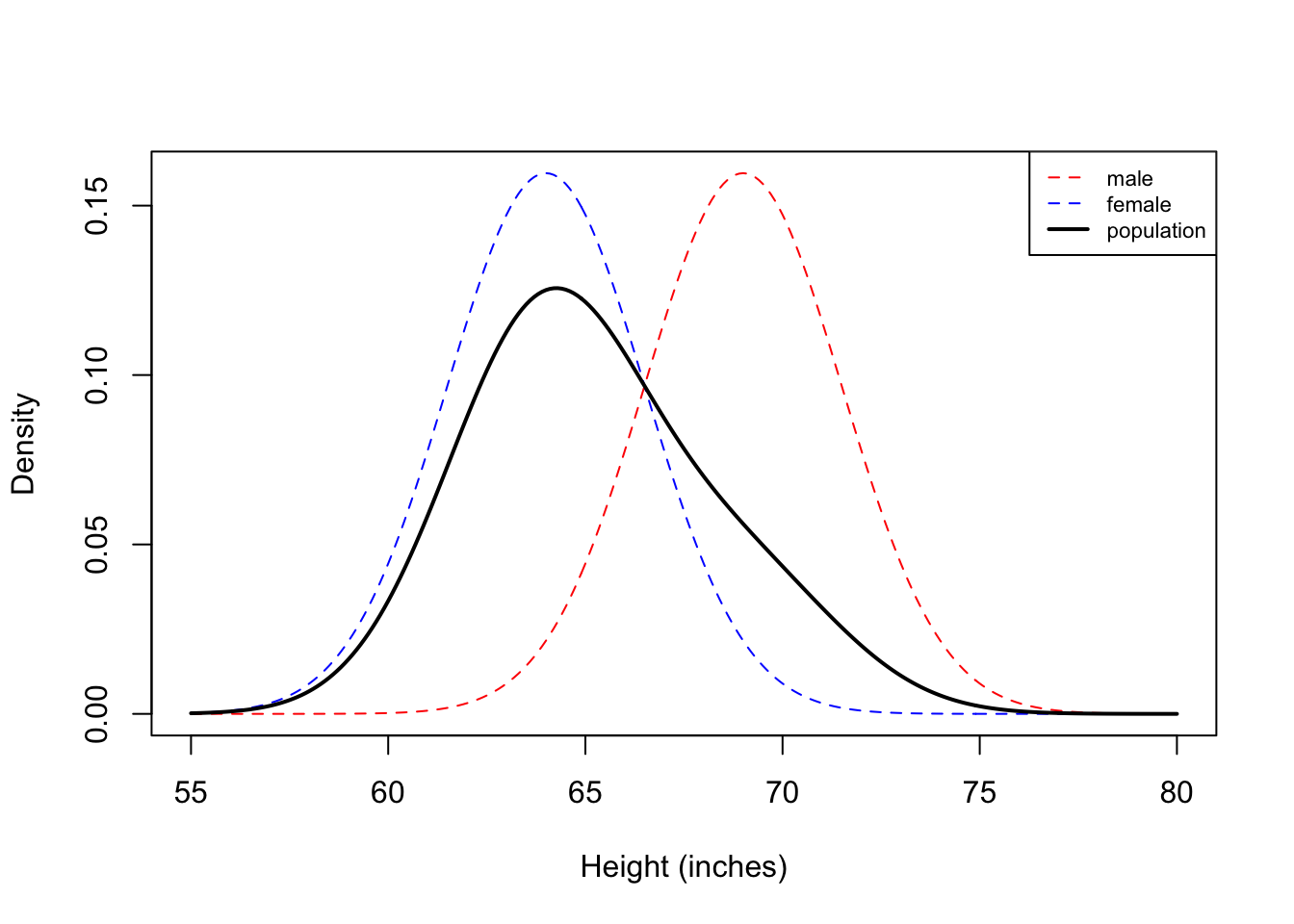
Mixture Model Example . Gaussian mixture models (gmms) are statistical models that represent the data as a mixture of gaussian (normal) distributions. Sklearn.mixture is a package which enables one to learn gaussian mixture models (diagonal, spherical, tied and full covariance matrices supported), sample them, and estimate. (x) = w1f1(x) + (1 − w1)f2(x) where f1 and f2 are gaussians. Mixture of two gaussians is a distribution whose density function is: Understand the complex concepts of the gaussian mixture model and learn to implement it from scratch with clear and concise explanations. In mixture models, p(z) is always a multinomial distribution. P(x j z) can take a variety of parametric forms, but for this lecture we'll.
from stephens999.github.io
Understand the complex concepts of the gaussian mixture model and learn to implement it from scratch with clear and concise explanations. P(x j z) can take a variety of parametric forms, but for this lecture we'll. Gaussian mixture models (gmms) are statistical models that represent the data as a mixture of gaussian (normal) distributions. Sklearn.mixture is a package which enables one to learn gaussian mixture models (diagonal, spherical, tied and full covariance matrices supported), sample them, and estimate. In mixture models, p(z) is always a multinomial distribution. Mixture of two gaussians is a distribution whose density function is: (x) = w1f1(x) + (1 − w1)f2(x) where f1 and f2 are gaussians.
Introduction to Mixture Models
Mixture Model Example (x) = w1f1(x) + (1 − w1)f2(x) where f1 and f2 are gaussians. (x) = w1f1(x) + (1 − w1)f2(x) where f1 and f2 are gaussians. P(x j z) can take a variety of parametric forms, but for this lecture we'll. Sklearn.mixture is a package which enables one to learn gaussian mixture models (diagonal, spherical, tied and full covariance matrices supported), sample them, and estimate. In mixture models, p(z) is always a multinomial distribution. Understand the complex concepts of the gaussian mixture model and learn to implement it from scratch with clear and concise explanations. Gaussian mixture models (gmms) are statistical models that represent the data as a mixture of gaussian (normal) distributions. Mixture of two gaussians is a distribution whose density function is:
From www.storyboardthat.com
Modeling Elements, Compounds and Mixtures Storyboard Mixture Model Example Gaussian mixture models (gmms) are statistical models that represent the data as a mixture of gaussian (normal) distributions. Understand the complex concepts of the gaussian mixture model and learn to implement it from scratch with clear and concise explanations. (x) = w1f1(x) + (1 − w1)f2(x) where f1 and f2 are gaussians. Sklearn.mixture is a package which enables one to. Mixture Model Example.
From www.youtube.com
Pure Substances, Elements, Compounds, Homogenous & Heterogenous Mixture Mixture Model Example Sklearn.mixture is a package which enables one to learn gaussian mixture models (diagonal, spherical, tied and full covariance matrices supported), sample them, and estimate. Mixture of two gaussians is a distribution whose density function is: (x) = w1f1(x) + (1 − w1)f2(x) where f1 and f2 are gaussians. Understand the complex concepts of the gaussian mixture model and learn to. Mixture Model Example.
From stephens999.github.io
Introduction to Mixture Models Mixture Model Example Mixture of two gaussians is a distribution whose density function is: Sklearn.mixture is a package which enables one to learn gaussian mixture models (diagonal, spherical, tied and full covariance matrices supported), sample them, and estimate. P(x j z) can take a variety of parametric forms, but for this lecture we'll. In mixture models, p(z) is always a multinomial distribution. Understand. Mixture Model Example.
From www.geeksforgeeks.org
What is a Mixture? Definition, Properties, Examples, Types and FAQs Mixture Model Example Mixture of two gaussians is a distribution whose density function is: Sklearn.mixture is a package which enables one to learn gaussian mixture models (diagonal, spherical, tied and full covariance matrices supported), sample them, and estimate. Gaussian mixture models (gmms) are statistical models that represent the data as a mixture of gaussian (normal) distributions. Understand the complex concepts of the gaussian. Mixture Model Example.
From www.slideserve.com
PPT Gaussian Mixture Model PowerPoint Presentation, free download Mixture Model Example (x) = w1f1(x) + (1 − w1)f2(x) where f1 and f2 are gaussians. P(x j z) can take a variety of parametric forms, but for this lecture we'll. Sklearn.mixture is a package which enables one to learn gaussian mixture models (diagonal, spherical, tied and full covariance matrices supported), sample them, and estimate. Mixture of two gaussians is a distribution whose. Mixture Model Example.
From sciencenotes.org
What Is a Mixture in Chemistry? Definition and Examples Mixture Model Example P(x j z) can take a variety of parametric forms, but for this lecture we'll. Understand the complex concepts of the gaussian mixture model and learn to implement it from scratch with clear and concise explanations. Mixture of two gaussians is a distribution whose density function is: Sklearn.mixture is a package which enables one to learn gaussian mixture models (diagonal,. Mixture Model Example.
From www.yaclass.in
Types of mixture Homogeneous and Heterogeneous — lesson. Science State Mixture Model Example In mixture models, p(z) is always a multinomial distribution. P(x j z) can take a variety of parametric forms, but for this lecture we'll. Gaussian mixture models (gmms) are statistical models that represent the data as a mixture of gaussian (normal) distributions. Sklearn.mixture is a package which enables one to learn gaussian mixture models (diagonal, spherical, tied and full covariance. Mixture Model Example.
From acamrmicheal.weebly.com
Properties of Mixtures ACA Grade 8 Science Mixture Model Example In mixture models, p(z) is always a multinomial distribution. Understand the complex concepts of the gaussian mixture model and learn to implement it from scratch with clear and concise explanations. P(x j z) can take a variety of parametric forms, but for this lecture we'll. Mixture of two gaussians is a distribution whose density function is: Gaussian mixture models (gmms). Mixture Model Example.
From en.wikipedia.org
Mixture model Wikipedia Mixture Model Example In mixture models, p(z) is always a multinomial distribution. P(x j z) can take a variety of parametric forms, but for this lecture we'll. (x) = w1f1(x) + (1 − w1)f2(x) where f1 and f2 are gaussians. Gaussian mixture models (gmms) are statistical models that represent the data as a mixture of gaussian (normal) distributions. Understand the complex concepts of. Mixture Model Example.
From herbalic79.blogspot.com
Element Compound Mixture Diagram Worksheet Herbalic Mixture Model Example Sklearn.mixture is a package which enables one to learn gaussian mixture models (diagonal, spherical, tied and full covariance matrices supported), sample them, and estimate. In mixture models, p(z) is always a multinomial distribution. Mixture of two gaussians is a distribution whose density function is: P(x j z) can take a variety of parametric forms, but for this lecture we'll. Gaussian. Mixture Model Example.
From www.thoughtco.com
Mixture Definition and Examples in Science Mixture Model Example (x) = w1f1(x) + (1 − w1)f2(x) where f1 and f2 are gaussians. Mixture of two gaussians is a distribution whose density function is: In mixture models, p(z) is always a multinomial distribution. Understand the complex concepts of the gaussian mixture model and learn to implement it from scratch with clear and concise explanations. P(x j z) can take a. Mixture Model Example.
From www.expii.com
Homogeneous vs. Heterogeneous Mixtures — A Comparison Expii Mixture Model Example Understand the complex concepts of the gaussian mixture model and learn to implement it from scratch with clear and concise explanations. Gaussian mixture models (gmms) are statistical models that represent the data as a mixture of gaussian (normal) distributions. Sklearn.mixture is a package which enables one to learn gaussian mixture models (diagonal, spherical, tied and full covariance matrices supported), sample. Mixture Model Example.
From www.teachoo.com
Homogeneous and Hetrogeneous Mixtures Definition, Examples Teachoo Mixture Model Example Mixture of two gaussians is a distribution whose density function is: P(x j z) can take a variety of parametric forms, but for this lecture we'll. Sklearn.mixture is a package which enables one to learn gaussian mixture models (diagonal, spherical, tied and full covariance matrices supported), sample them, and estimate. (x) = w1f1(x) + (1 − w1)f2(x) where f1 and. Mixture Model Example.
From www.slideserve.com
PPT Univariate Gaussian Mixture Model PowerPoint Presentation, free Mixture Model Example Mixture of two gaussians is a distribution whose density function is: Understand the complex concepts of the gaussian mixture model and learn to implement it from scratch with clear and concise explanations. (x) = w1f1(x) + (1 − w1)f2(x) where f1 and f2 are gaussians. Sklearn.mixture is a package which enables one to learn gaussian mixture models (diagonal, spherical, tied. Mixture Model Example.
From www.slideserve.com
PPT Mixture Models And Expectation Maximization PowerPoint Mixture Model Example (x) = w1f1(x) + (1 − w1)f2(x) where f1 and f2 are gaussians. Mixture of two gaussians is a distribution whose density function is: Gaussian mixture models (gmms) are statistical models that represent the data as a mixture of gaussian (normal) distributions. P(x j z) can take a variety of parametric forms, but for this lecture we'll. In mixture models,. Mixture Model Example.
From ryanwingate.com
Gaussian Mixture Model Examples Mixture Model Example Mixture of two gaussians is a distribution whose density function is: Gaussian mixture models (gmms) are statistical models that represent the data as a mixture of gaussian (normal) distributions. P(x j z) can take a variety of parametric forms, but for this lecture we'll. Sklearn.mixture is a package which enables one to learn gaussian mixture models (diagonal, spherical, tied and. Mixture Model Example.
From www.slideserve.com
PPT Univariate Gaussian Mixture Model PowerPoint Presentation, free Mixture Model Example Gaussian mixture models (gmms) are statistical models that represent the data as a mixture of gaussian (normal) distributions. Mixture of two gaussians is a distribution whose density function is: In mixture models, p(z) is always a multinomial distribution. Sklearn.mixture is a package which enables one to learn gaussian mixture models (diagonal, spherical, tied and full covariance matrices supported), sample them,. Mixture Model Example.
From www.researchgate.net
Mixture model example. An illustration of a three component binomial Mixture Model Example Sklearn.mixture is a package which enables one to learn gaussian mixture models (diagonal, spherical, tied and full covariance matrices supported), sample them, and estimate. P(x j z) can take a variety of parametric forms, but for this lecture we'll. Mixture of two gaussians is a distribution whose density function is: Gaussian mixture models (gmms) are statistical models that represent the. Mixture Model Example.
From www.dreamstime.com
Mixtures of Both Elements and Compounds Stock Vector Illustration of Mixture Model Example (x) = w1f1(x) + (1 − w1)f2(x) where f1 and f2 are gaussians. Sklearn.mixture is a package which enables one to learn gaussian mixture models (diagonal, spherical, tied and full covariance matrices supported), sample them, and estimate. P(x j z) can take a variety of parametric forms, but for this lecture we'll. Mixture of two gaussians is a distribution whose. Mixture Model Example.
From primaryleap.co.uk
Chemistry Solutions And Mixtures Level 1 activity for kids Mixture Model Example P(x j z) can take a variety of parametric forms, but for this lecture we'll. Gaussian mixture models (gmms) are statistical models that represent the data as a mixture of gaussian (normal) distributions. Sklearn.mixture is a package which enables one to learn gaussian mixture models (diagonal, spherical, tied and full covariance matrices supported), sample them, and estimate. Understand the complex. Mixture Model Example.
From www.slideserve.com
PPT Gaussian Mixture Models PowerPoint Presentation, free download Mixture Model Example Mixture of two gaussians is a distribution whose density function is: (x) = w1f1(x) + (1 − w1)f2(x) where f1 and f2 are gaussians. P(x j z) can take a variety of parametric forms, but for this lecture we'll. In mixture models, p(z) is always a multinomial distribution. Sklearn.mixture is a package which enables one to learn gaussian mixture models. Mixture Model Example.
From www.slideserve.com
PPT Mixture Models And Expectation Maximization PowerPoint Mixture Model Example P(x j z) can take a variety of parametric forms, but for this lecture we'll. (x) = w1f1(x) + (1 − w1)f2(x) where f1 and f2 are gaussians. Sklearn.mixture is a package which enables one to learn gaussian mixture models (diagonal, spherical, tied and full covariance matrices supported), sample them, and estimate. In mixture models, p(z) is always a multinomial. Mixture Model Example.
From www.teachoo.com
What is a Mixture? Types of Mixtures Chemistry Teachoo Mixture Model Example Gaussian mixture models (gmms) are statistical models that represent the data as a mixture of gaussian (normal) distributions. Sklearn.mixture is a package which enables one to learn gaussian mixture models (diagonal, spherical, tied and full covariance matrices supported), sample them, and estimate. (x) = w1f1(x) + (1 − w1)f2(x) where f1 and f2 are gaussians. P(x j z) can take. Mixture Model Example.
From animalia-life.club
Mixtures Examples Mixture Model Example P(x j z) can take a variety of parametric forms, but for this lecture we'll. Gaussian mixture models (gmms) are statistical models that represent the data as a mixture of gaussian (normal) distributions. Understand the complex concepts of the gaussian mixture model and learn to implement it from scratch with clear and concise explanations. Sklearn.mixture is a package which enables. Mixture Model Example.
From ryanwingate.com
Gaussian Mixture Model Examples Mixture Model Example Sklearn.mixture is a package which enables one to learn gaussian mixture models (diagonal, spherical, tied and full covariance matrices supported), sample them, and estimate. Mixture of two gaussians is a distribution whose density function is: Gaussian mixture models (gmms) are statistical models that represent the data as a mixture of gaussian (normal) distributions. In mixture models, p(z) is always a. Mixture Model Example.
From www.shiksha.com
Gaussian Mixture Model Examples, Advantages and Disadvantages Mixture Model Example Understand the complex concepts of the gaussian mixture model and learn to implement it from scratch with clear and concise explanations. Mixture of two gaussians is a distribution whose density function is: Gaussian mixture models (gmms) are statistical models that represent the data as a mixture of gaussian (normal) distributions. P(x j z) can take a variety of parametric forms,. Mixture Model Example.
From www.researchgate.net
Gaussian mixture model in the porosityvelocity domain. In this Mixture Model Example Understand the complex concepts of the gaussian mixture model and learn to implement it from scratch with clear and concise explanations. (x) = w1f1(x) + (1 − w1)f2(x) where f1 and f2 are gaussians. In mixture models, p(z) is always a multinomial distribution. Mixture of two gaussians is a distribution whose density function is: Sklearn.mixture is a package which enables. Mixture Model Example.
From imagetou.com
Gaussian Mixture Model Example Step By Step Image to u Mixture Model Example In mixture models, p(z) is always a multinomial distribution. P(x j z) can take a variety of parametric forms, but for this lecture we'll. Mixture of two gaussians is a distribution whose density function is: (x) = w1f1(x) + (1 − w1)f2(x) where f1 and f2 are gaussians. Understand the complex concepts of the gaussian mixture model and learn to. Mixture Model Example.
From sciencenotes.org
10 Examples of Mixtures Mixture Model Example (x) = w1f1(x) + (1 − w1)f2(x) where f1 and f2 are gaussians. Understand the complex concepts of the gaussian mixture model and learn to implement it from scratch with clear and concise explanations. In mixture models, p(z) is always a multinomial distribution. Gaussian mixture models (gmms) are statistical models that represent the data as a mixture of gaussian (normal). Mixture Model Example.
From sciencenotes.org
What Is a Homogeneous Mixture? Definition and Examples Mixture Model Example Understand the complex concepts of the gaussian mixture model and learn to implement it from scratch with clear and concise explanations. Sklearn.mixture is a package which enables one to learn gaussian mixture models (diagonal, spherical, tied and full covariance matrices supported), sample them, and estimate. (x) = w1f1(x) + (1 − w1)f2(x) where f1 and f2 are gaussians. Gaussian mixture. Mixture Model Example.
From www.slideserve.com
PPT Mixture Models And Expectation Maximization PowerPoint Mixture Model Example Understand the complex concepts of the gaussian mixture model and learn to implement it from scratch with clear and concise explanations. P(x j z) can take a variety of parametric forms, but for this lecture we'll. Mixture of two gaussians is a distribution whose density function is: Gaussian mixture models (gmms) are statistical models that represent the data as a. Mixture Model Example.
From www.vedantu.com
Chemical Mixtures Learn Definition, Types and Examples Mixture Model Example Understand the complex concepts of the gaussian mixture model and learn to implement it from scratch with clear and concise explanations. Sklearn.mixture is a package which enables one to learn gaussian mixture models (diagonal, spherical, tied and full covariance matrices supported), sample them, and estimate. Mixture of two gaussians is a distribution whose density function is: P(x j z) can. Mixture Model Example.
From sciencetrends.com
5 Examples Of Homogeneous Mixture For Chemistry Class Science Trends Mixture Model Example Understand the complex concepts of the gaussian mixture model and learn to implement it from scratch with clear and concise explanations. Sklearn.mixture is a package which enables one to learn gaussian mixture models (diagonal, spherical, tied and full covariance matrices supported), sample them, and estimate. (x) = w1f1(x) + (1 − w1)f2(x) where f1 and f2 are gaussians. Mixture of. Mixture Model Example.
From fizzy.cc
Gaussian Mixture Model Mixture Model Example P(x j z) can take a variety of parametric forms, but for this lecture we'll. Sklearn.mixture is a package which enables one to learn gaussian mixture models (diagonal, spherical, tied and full covariance matrices supported), sample them, and estimate. In mixture models, p(z) is always a multinomial distribution. Gaussian mixture models (gmms) are statistical models that represent the data as. Mixture Model Example.
From www.thoughtco.com
10 Heterogeneous and Homogeneous Mixtures Mixture Model Example Sklearn.mixture is a package which enables one to learn gaussian mixture models (diagonal, spherical, tied and full covariance matrices supported), sample them, and estimate. P(x j z) can take a variety of parametric forms, but for this lecture we'll. (x) = w1f1(x) + (1 − w1)f2(x) where f1 and f2 are gaussians. Mixture of two gaussians is a distribution whose. Mixture Model Example.