Are Triangles Ratio . So when the lengths are twice as long, the area is four times as. We know the side 6.4 in triangle s. There are 4 squares, 5 triangles and 2 circles. In this example we can see that: If two triangles have two pairs of sides in the same ratio and the included angles are also equal, then the triangles are similar. The ratio of the number of squares to triangles to circles is 4 : The 3 important ratios are known as the sine (sin),. Trigonometric ratios show how long one side of the triangle is compared to another. The 6.4 faces the angle marked with two arcs as does the side of length 8 in triangle r. The answer is simple if we just draw in three more lines: Two triangles are similar if the angles are the same size or the corresponding sides are in the same ratio. One pair of sides is in. Either of these conditions will prove. We know all the sides in triangle r, and. We can see that the small triangle fits into the big triangle four times.
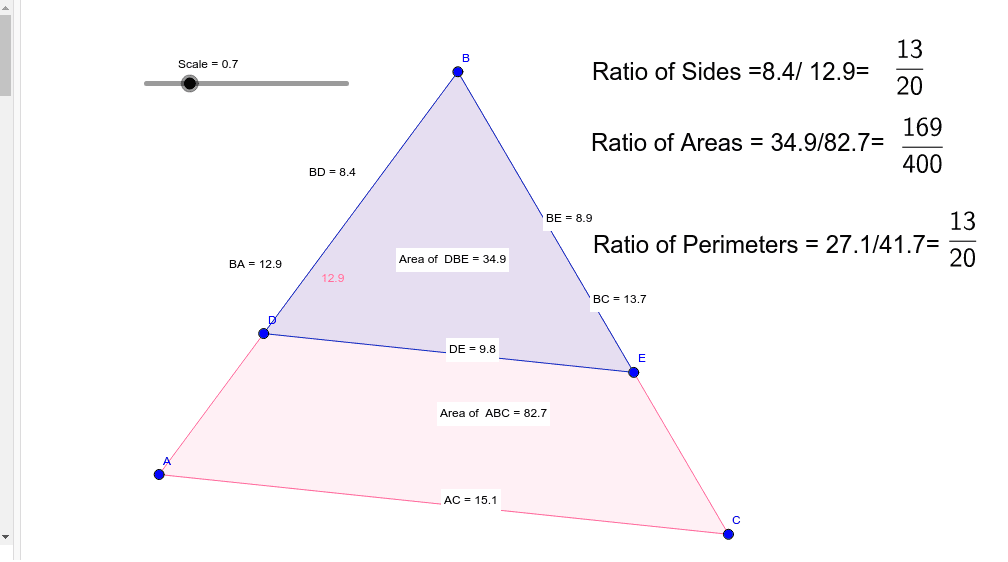
from www.geogebra.org
We know the side 6.4 in triangle s. Either of these conditions will prove. The 6.4 faces the angle marked with two arcs as does the side of length 8 in triangle r. Trigonometric ratios show how long one side of the triangle is compared to another. In this example we can see that: The 3 important ratios are known as the sine (sin),. There are 4 squares, 5 triangles and 2 circles. If two triangles have two pairs of sides in the same ratio and the included angles are also equal, then the triangles are similar. Two triangles are similar if the angles are the same size or the corresponding sides are in the same ratio. The ratio of the number of squares to triangles to circles is 4 :
Similar triangles area ratio GeoGebra
Are Triangles Ratio Trigonometric ratios show how long one side of the triangle is compared to another. If two triangles have two pairs of sides in the same ratio and the included angles are also equal, then the triangles are similar. One pair of sides is in. The ratio of the number of squares to triangles to circles is 4 : Trigonometric ratios show how long one side of the triangle is compared to another. We know the side 6.4 in triangle s. There are 4 squares, 5 triangles and 2 circles. We know all the sides in triangle r, and. Either of these conditions will prove. Two triangles are similar if the angles are the same size or the corresponding sides are in the same ratio. In this example we can see that: The 6.4 faces the angle marked with two arcs as does the side of length 8 in triangle r. The 3 important ratios are known as the sine (sin),. We can see that the small triangle fits into the big triangle four times. So when the lengths are twice as long, the area is four times as. The answer is simple if we just draw in three more lines:
From www.slideserve.com
PPT Trigonometric Ratios Triangles in Quadrant I PowerPoint Are Triangles Ratio The 3 important ratios are known as the sine (sin),. The ratio of the number of squares to triangles to circles is 4 : Trigonometric ratios show how long one side of the triangle is compared to another. We can see that the small triangle fits into the big triangle four times. In this example we can see that: The. Are Triangles Ratio.
From www.teachoo.com
Question 6 Prove that ratio of areas of two similar triangles Are Triangles Ratio In this example we can see that: The 3 important ratios are known as the sine (sin),. If two triangles have two pairs of sides in the same ratio and the included angles are also equal, then the triangles are similar. The 6.4 faces the angle marked with two arcs as does the side of length 8 in triangle r.. Are Triangles Ratio.
From calcworkshop.com
Special Right Triangles (Fully Explained w/ 19 Examples!) Are Triangles Ratio We know the side 6.4 in triangle s. The 6.4 faces the angle marked with two arcs as does the side of length 8 in triangle r. The 3 important ratios are known as the sine (sin),. The ratio of the number of squares to triangles to circles is 4 : If two triangles have two pairs of sides in. Are Triangles Ratio.
From www.slideserve.com
PPT Trigonometric Ratios in Right Triangles PowerPoint Presentation Are Triangles Ratio We know the side 6.4 in triangle s. One pair of sides is in. Trigonometric ratios show how long one side of the triangle is compared to another. There are 4 squares, 5 triangles and 2 circles. So when the lengths are twice as long, the area is four times as. The 6.4 faces the angle marked with two arcs. Are Triangles Ratio.
From www.onlinemathlearning.com
Similarity and Trig Ratios (examples, solutions, videos, lessons Are Triangles Ratio We can see that the small triangle fits into the big triangle four times. Trigonometric ratios show how long one side of the triangle is compared to another. Two triangles are similar if the angles are the same size or the corresponding sides are in the same ratio. The answer is simple if we just draw in three more lines:. Are Triangles Ratio.
From www.youtube.com
Right Triangle Trigonometry Finding the Six Trigonometric Ratios YouTube Are Triangles Ratio The ratio of the number of squares to triangles to circles is 4 : Two triangles are similar if the angles are the same size or the corresponding sides are in the same ratio. We can see that the small triangle fits into the big triangle four times. The answer is simple if we just draw in three more lines:. Are Triangles Ratio.
From study.com
How to Find Trigonometric Ratios Given a Right Triangle Trigonometry Are Triangles Ratio There are 4 squares, 5 triangles and 2 circles. We can see that the small triangle fits into the big triangle four times. In this example we can see that: Two triangles are similar if the angles are the same size or the corresponding sides are in the same ratio. So when the lengths are twice as long, the area. Are Triangles Ratio.
From manga.pakasak.com
Trigonometric Ratios Definition, Formulas, Table, Examples, and FAQs Are Triangles Ratio The ratio of the number of squares to triangles to circles is 4 : If two triangles have two pairs of sides in the same ratio and the included angles are also equal, then the triangles are similar. Either of these conditions will prove. We know all the sides in triangle r, and. So when the lengths are twice as. Are Triangles Ratio.
From www.youtube.com
The ratio of two side lengths of a triangle are given. Solve for the Are Triangles Ratio So when the lengths are twice as long, the area is four times as. We know the side 6.4 in triangle s. We know all the sides in triangle r, and. The 3 important ratios are known as the sine (sin),. Two triangles are similar if the angles are the same size or the corresponding sides are in the same. Are Triangles Ratio.
From www.teachoo.com
Theorem 6.6 Class 10 Ratio of areas of two similar triangles Are Triangles Ratio So when the lengths are twice as long, the area is four times as. We know the side 6.4 in triangle s. The ratio of the number of squares to triangles to circles is 4 : Trigonometric ratios show how long one side of the triangle is compared to another. The 6.4 faces the angle marked with two arcs as. Are Triangles Ratio.
From owlcation.com
Triangle Proportionality Theorem (With Proof and Examples) Owlcation Are Triangles Ratio The 3 important ratios are known as the sine (sin),. The ratio of the number of squares to triangles to circles is 4 : Two triangles are similar if the angles are the same size or the corresponding sides are in the same ratio. So when the lengths are twice as long, the area is four times as. We know. Are Triangles Ratio.
From www.youtube.com
Special Triangles & Trig Ratios • [2.1c] PreCalculus 11 YouTube Are Triangles Ratio The answer is simple if we just draw in three more lines: We know the side 6.4 in triangle s. In this example we can see that: The ratio of the number of squares to triangles to circles is 4 : We know all the sides in triangle r, and. We can see that the small triangle fits into the. Are Triangles Ratio.
From www.geogebra.org
Similar triangles area ratio GeoGebra Are Triangles Ratio The ratio of the number of squares to triangles to circles is 4 : Trigonometric ratios show how long one side of the triangle is compared to another. We can see that the small triangle fits into the big triangle four times. The answer is simple if we just draw in three more lines: So when the lengths are twice. Are Triangles Ratio.
From www.pinterest.com
Similar Triangles , Area and Perimeter High school math, Math Are Triangles Ratio Trigonometric ratios show how long one side of the triangle is compared to another. We can see that the small triangle fits into the big triangle four times. One pair of sides is in. We know the side 6.4 in triangle s. If two triangles have two pairs of sides in the same ratio and the included angles are also. Are Triangles Ratio.
From www.cuemath.com
Trigonometric ratios Identities Formulas Table Examples Cuemath Are Triangles Ratio The ratio of the number of squares to triangles to circles is 4 : Trigonometric ratios show how long one side of the triangle is compared to another. There are 4 squares, 5 triangles and 2 circles. The 3 important ratios are known as the sine (sin),. One pair of sides is in. Either of these conditions will prove. We. Are Triangles Ratio.
From calcworkshop.com
Special Right Triangles (Fully Explained w/ 19 Examples!) Are Triangles Ratio Trigonometric ratios show how long one side of the triangle is compared to another. The answer is simple if we just draw in three more lines: We know all the sides in triangle r, and. Either of these conditions will prove. We know the side 6.4 in triangle s. We can see that the small triangle fits into the big. Are Triangles Ratio.
From owlcation.com
Triangle Proportionality Theorem (With Proof and Examples) Owlcation Are Triangles Ratio We can see that the small triangle fits into the big triangle four times. If two triangles have two pairs of sides in the same ratio and the included angles are also equal, then the triangles are similar. The ratio of the number of squares to triangles to circles is 4 : We know all the sides in triangle r,. Are Triangles Ratio.
From owlcation.com
Triangle Proportionality Theorem (With Proof and Examples) Owlcation Are Triangles Ratio Either of these conditions will prove. We can see that the small triangle fits into the big triangle four times. The 3 important ratios are known as the sine (sin),. We know all the sides in triangle r, and. Two triangles are similar if the angles are the same size or the corresponding sides are in the same ratio. In. Are Triangles Ratio.
From intomath.org
Lesson 5 Right Triangle Trigonometry. Trig ratios IntoMath Are Triangles Ratio The 6.4 faces the angle marked with two arcs as does the side of length 8 in triangle r. Either of these conditions will prove. If two triangles have two pairs of sides in the same ratio and the included angles are also equal, then the triangles are similar. One pair of sides is in. Two triangles are similar if. Are Triangles Ratio.
From www.youtube.com
MPM2D Trigonometry Primary Trigonometric Ratios in Right Triangles Are Triangles Ratio If two triangles have two pairs of sides in the same ratio and the included angles are also equal, then the triangles are similar. We can see that the small triangle fits into the big triangle four times. The 6.4 faces the angle marked with two arcs as does the side of length 8 in triangle r. In this example. Are Triangles Ratio.
From study.com
Proportional Triangles Corresponding Angles & Opposite Sides Lesson Are Triangles Ratio One pair of sides is in. We know the side 6.4 in triangle s. If two triangles have two pairs of sides in the same ratio and the included angles are also equal, then the triangles are similar. The ratio of the number of squares to triangles to circles is 4 : Trigonometric ratios show how long one side of. Are Triangles Ratio.
From www.grc.nasa.gov
Ratios in Triangles Are Triangles Ratio The 3 important ratios are known as the sine (sin),. We know the side 6.4 in triangle s. The 6.4 faces the angle marked with two arcs as does the side of length 8 in triangle r. The ratio of the number of squares to triangles to circles is 4 : Two triangles are similar if the angles are the. Are Triangles Ratio.
From www.geogebra.org
Properties of the ratio of areas of triangles GeoGebra Are Triangles Ratio So when the lengths are twice as long, the area is four times as. The answer is simple if we just draw in three more lines: One pair of sides is in. We can see that the small triangle fits into the big triangle four times. We know the side 6.4 in triangle s. The 6.4 faces the angle marked. Are Triangles Ratio.
From www.youtube.com
Proof that the corresponding sides of similar triangles are in the same Are Triangles Ratio Two triangles are similar if the angles are the same size or the corresponding sides are in the same ratio. Trigonometric ratios show how long one side of the triangle is compared to another. So when the lengths are twice as long, the area is four times as. If two triangles have two pairs of sides in the same ratio. Are Triangles Ratio.
From www.youtube.com
Ratio of areas of two similar triangles equals ratio of square of any Are Triangles Ratio Either of these conditions will prove. The 6.4 faces the angle marked with two arcs as does the side of length 8 in triangle r. In this example we can see that: One pair of sides is in. The ratio of the number of squares to triangles to circles is 4 : There are 4 squares, 5 triangles and 2. Are Triangles Ratio.
From donsteward.blogspot.com
MEDIAN Don Steward mathematics teaching triangle angles in a ratio Are Triangles Ratio The 6.4 faces the angle marked with two arcs as does the side of length 8 in triangle r. Two triangles are similar if the angles are the same size or the corresponding sides are in the same ratio. The 3 important ratios are known as the sine (sin),. There are 4 squares, 5 triangles and 2 circles. The answer. Are Triangles Ratio.
From donsteward.blogspot.com
MEDIAN Don Steward mathematics teaching exact trigonometric values Are Triangles Ratio There are 4 squares, 5 triangles and 2 circles. If two triangles have two pairs of sides in the same ratio and the included angles are also equal, then the triangles are similar. The ratio of the number of squares to triangles to circles is 4 : We know the side 6.4 in triangle s. The answer is simple if. Are Triangles Ratio.
From www.teachoo.com
The sides of two similar triangles are in the ratio 2 3, then area Are Triangles Ratio So when the lengths are twice as long, the area is four times as. In this example we can see that: Two triangles are similar if the angles are the same size or the corresponding sides are in the same ratio. The 3 important ratios are known as the sine (sin),. Trigonometric ratios show how long one side of the. Are Triangles Ratio.
From www.ck12.org
Trigonometric Ratios on the Unit Circle CK12 Foundation Are Triangles Ratio We know all the sides in triangle r, and. Two triangles are similar if the angles are the same size or the corresponding sides are in the same ratio. There are 4 squares, 5 triangles and 2 circles. The answer is simple if we just draw in three more lines: We can see that the small triangle fits into the. Are Triangles Ratio.
From donsteward.blogspot.com
MEDIAN Don Steward mathematics teaching triangle angles in a ratio Are Triangles Ratio If two triangles have two pairs of sides in the same ratio and the included angles are also equal, then the triangles are similar. Either of these conditions will prove. The 3 important ratios are known as the sine (sin),. The 6.4 faces the angle marked with two arcs as does the side of length 8 in triangle r. One. Are Triangles Ratio.
From www.youtube.com
Ratio of the Areas of two Similar Triangles Similarity of Triangles Are Triangles Ratio Either of these conditions will prove. We know the side 6.4 in triangle s. The 6.4 faces the angle marked with two arcs as does the side of length 8 in triangle r. So when the lengths are twice as long, the area is four times as. The 3 important ratios are known as the sine (sin),. We can see. Are Triangles Ratio.
From www.slideserve.com
PPT Trigonometric Ratios in Right Triangles PowerPoint Presentation Are Triangles Ratio Either of these conditions will prove. If two triangles have two pairs of sides in the same ratio and the included angles are also equal, then the triangles are similar. The 3 important ratios are known as the sine (sin),. We know the side 6.4 in triangle s. Trigonometric ratios show how long one side of the triangle is compared. Are Triangles Ratio.
From firmfunda.com
Trigonometry (Introduction) Trigonometric Ratios Explained Are Triangles Ratio We know the side 6.4 in triangle s. The 3 important ratios are known as the sine (sin),. The 6.4 faces the angle marked with two arcs as does the side of length 8 in triangle r. The answer is simple if we just draw in three more lines: The ratio of the number of squares to triangles to circles. Are Triangles Ratio.
From igcseatmathematicsrealm.blogspot.co.uk
Trigonometrical Ratios IGCSE at Mathematics Realm Are Triangles Ratio In this example we can see that: The ratio of the number of squares to triangles to circles is 4 : The 6.4 faces the angle marked with two arcs as does the side of length 8 in triangle r. The answer is simple if we just draw in three more lines: We can see that the small triangle fits. Are Triangles Ratio.
From www.youtube.com
Proportional Parts of Similar Triangles YouTube Are Triangles Ratio The 3 important ratios are known as the sine (sin),. One pair of sides is in. The ratio of the number of squares to triangles to circles is 4 : We know the side 6.4 in triangle s. We can see that the small triangle fits into the big triangle four times. So when the lengths are twice as long,. Are Triangles Ratio.