Copper Wire Magnetic Force . To investigate this force, let’s consider the. I i — current flowing. F = qvdb sin θ (21.5.3) (21.5.3) f = q v d b sin θ. Assuming that our wire is straight and very long, we can estimate a magnetic field around the wire with the following equation: When the connection in the copper wire is replaced by the led and ben drops the magnet through the. The force (f) a magnetic field (b) exerts on an individual charge (q) traveling at drift velocity v d is: In this instance, θ represents the angle between. Wire losses of high frequency currents due to skin effects inside the wire which force high frequency current to flow on the outside surface of the. B = \frac {\mu_0 i} {2\pi d} b = 2πdμ0i.
from www.alamy.com
Assuming that our wire is straight and very long, we can estimate a magnetic field around the wire with the following equation: When the connection in the copper wire is replaced by the led and ben drops the magnet through the. Wire losses of high frequency currents due to skin effects inside the wire which force high frequency current to flow on the outside surface of the. To investigate this force, let’s consider the. F = qvdb sin θ (21.5.3) (21.5.3) f = q v d b sin θ. B = \frac {\mu_0 i} {2\pi d} b = 2πdμ0i. The force (f) a magnetic field (b) exerts on an individual charge (q) traveling at drift velocity v d is: I i — current flowing. In this instance, θ represents the angle between.
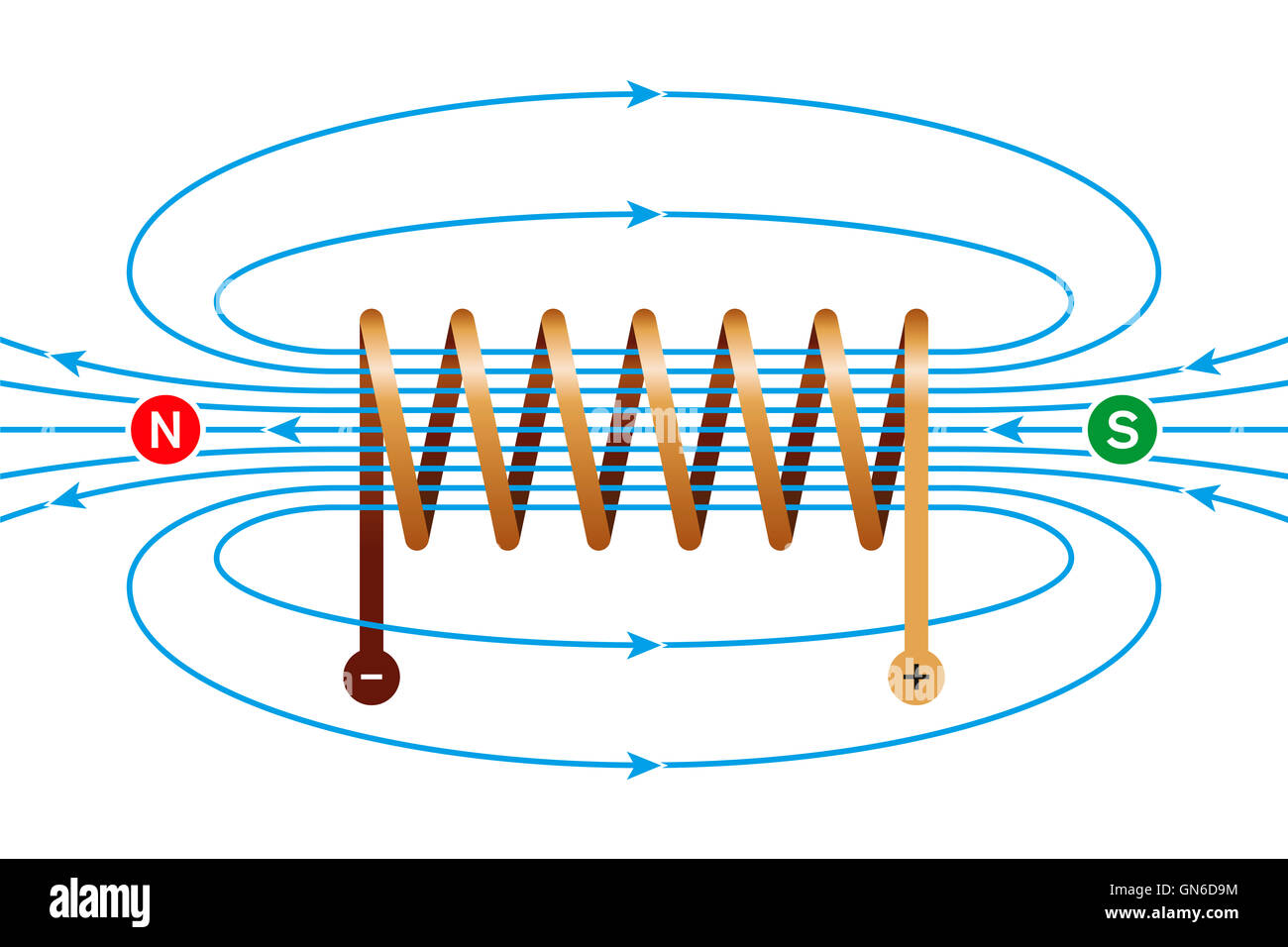
field of a currentcarrying coil. coil
Copper Wire Magnetic Force To investigate this force, let’s consider the. I i — current flowing. Assuming that our wire is straight and very long, we can estimate a magnetic field around the wire with the following equation: In this instance, θ represents the angle between. When the connection in the copper wire is replaced by the led and ben drops the magnet through the. Wire losses of high frequency currents due to skin effects inside the wire which force high frequency current to flow on the outside surface of the. F = qvdb sin θ (21.5.3) (21.5.3) f = q v d b sin θ. The force (f) a magnetic field (b) exerts on an individual charge (q) traveling at drift velocity v d is: To investigate this force, let’s consider the. B = \frac {\mu_0 i} {2\pi d} b = 2πdμ0i.
From www.youtube.com
A copper wire is held between the poles of a current in the Copper Wire Magnetic Force B = \frac {\mu_0 i} {2\pi d} b = 2πdμ0i. In this instance, θ represents the angle between. Assuming that our wire is straight and very long, we can estimate a magnetic field around the wire with the following equation: Wire losses of high frequency currents due to skin effects inside the wire which force high frequency current to flow. Copper Wire Magnetic Force.
From www.youtube.com
force between two current carrying wires and Ampere's Law Copper Wire Magnetic Force The force (f) a magnetic field (b) exerts on an individual charge (q) traveling at drift velocity v d is: Assuming that our wire is straight and very long, we can estimate a magnetic field around the wire with the following equation: When the connection in the copper wire is replaced by the led and ben drops the magnet through. Copper Wire Magnetic Force.
From lookgoodandstudyhard.blogspot.com
Physics Unit 11 / Look Good & Study Hard Copper Wire Magnetic Force In this instance, θ represents the angle between. The force (f) a magnetic field (b) exerts on an individual charge (q) traveling at drift velocity v d is: To investigate this force, let’s consider the. F = qvdb sin θ (21.5.3) (21.5.3) f = q v d b sin θ. B = \frac {\mu_0 i} {2\pi d} b = 2πdμ0i.. Copper Wire Magnetic Force.
From www.youtube.com
Field of a Coil YouTube Copper Wire Magnetic Force To investigate this force, let’s consider the. In this instance, θ represents the angle between. B = \frac {\mu_0 i} {2\pi d} b = 2πdμ0i. F = qvdb sin θ (21.5.3) (21.5.3) f = q v d b sin θ. When the connection in the copper wire is replaced by the led and ben drops the magnet through the. Assuming. Copper Wire Magnetic Force.
From electricalacademia.com
Force on a Current Carrying Conductor Electrical Academia Copper Wire Magnetic Force F = qvdb sin θ (21.5.3) (21.5.3) f = q v d b sin θ. The force (f) a magnetic field (b) exerts on an individual charge (q) traveling at drift velocity v d is: B = \frac {\mu_0 i} {2\pi d} b = 2πdμ0i. I i — current flowing. Wire losses of high frequency currents due to skin effects. Copper Wire Magnetic Force.
From www.alamy.com
Coil wire field lines hires stock photography and images Alamy Copper Wire Magnetic Force When the connection in the copper wire is replaced by the led and ben drops the magnet through the. Wire losses of high frequency currents due to skin effects inside the wire which force high frequency current to flow on the outside surface of the. In this instance, θ represents the angle between. To investigate this force, let’s consider the.. Copper Wire Magnetic Force.
From www.teachoo.com
[Physics Class 10] A copper wire is held between the poles of a Copper Wire Magnetic Force Assuming that our wire is straight and very long, we can estimate a magnetic field around the wire with the following equation: I i — current flowing. F = qvdb sin θ (21.5.3) (21.5.3) f = q v d b sin θ. In this instance, θ represents the angle between. The force (f) a magnetic field (b) exerts on an. Copper Wire Magnetic Force.
From blog.thepipingmart.com
Copper Wire An Overview Copper Wire Magnetic Force To investigate this force, let’s consider the. F = qvdb sin θ (21.5.3) (21.5.3) f = q v d b sin θ. I i — current flowing. B = \frac {\mu_0 i} {2\pi d} b = 2πdμ0i. In this instance, θ represents the angle between. Wire losses of high frequency currents due to skin effects inside the wire which force. Copper Wire Magnetic Force.
From www.livescience.com
Is copper Live Science Copper Wire Magnetic Force F = qvdb sin θ (21.5.3) (21.5.3) f = q v d b sin θ. I i — current flowing. To investigate this force, let’s consider the. Wire losses of high frequency currents due to skin effects inside the wire which force high frequency current to flow on the outside surface of the. Assuming that our wire is straight and. Copper Wire Magnetic Force.
From www.coursehero.com
[Solved] Calculate the length of the copper wire having a diameter of 1 Copper Wire Magnetic Force The force (f) a magnetic field (b) exerts on an individual charge (q) traveling at drift velocity v d is: I i — current flowing. Wire losses of high frequency currents due to skin effects inside the wire which force high frequency current to flow on the outside surface of the. When the connection in the copper wire is replaced. Copper Wire Magnetic Force.
From www.youtube.com
force on a currentcarrying copper rod YouTube Copper Wire Magnetic Force F = qvdb sin θ (21.5.3) (21.5.3) f = q v d b sin θ. The force (f) a magnetic field (b) exerts on an individual charge (q) traveling at drift velocity v d is: Wire losses of high frequency currents due to skin effects inside the wire which force high frequency current to flow on the outside surface of. Copper Wire Magnetic Force.
From www.youtube.com
FORCE ON A CURRENT CARRYING WIRE PLACED IN A FIELD YouTube Copper Wire Magnetic Force The force (f) a magnetic field (b) exerts on an individual charge (q) traveling at drift velocity v d is: When the connection in the copper wire is replaced by the led and ben drops the magnet through the. F = qvdb sin θ (21.5.3) (21.5.3) f = q v d b sin θ. Assuming that our wire is straight. Copper Wire Magnetic Force.
From studylib.net
Force on a CurrentCarrying Wire Copper Wire Magnetic Force When the connection in the copper wire is replaced by the led and ben drops the magnet through the. Wire losses of high frequency currents due to skin effects inside the wire which force high frequency current to flow on the outside surface of the. The force (f) a magnetic field (b) exerts on an individual charge (q) traveling at. Copper Wire Magnetic Force.
From www.lpenamelwire.com
Enamelled copper wire materials 16mm 20 Awg wire 4kg Copper Wire Magnetic Force In this instance, θ represents the angle between. B = \frac {\mu_0 i} {2\pi d} b = 2πdμ0i. The force (f) a magnetic field (b) exerts on an individual charge (q) traveling at drift velocity v d is: To investigate this force, let’s consider the. F = qvdb sin θ (21.5.3) (21.5.3) f = q v d b sin θ.. Copper Wire Magnetic Force.
From www.alamy.com
field wire filings hires stock photography and images Alamy Copper Wire Magnetic Force Assuming that our wire is straight and very long, we can estimate a magnetic field around the wire with the following equation: F = qvdb sin θ (21.5.3) (21.5.3) f = q v d b sin θ. B = \frac {\mu_0 i} {2\pi d} b = 2πdμ0i. The force (f) a magnetic field (b) exerts on an individual charge (q). Copper Wire Magnetic Force.
From byjus.com
A copper wire has a diameter of 0.5mm and resistivity of 16.2ohm metre Copper Wire Magnetic Force In this instance, θ represents the angle between. When the connection in the copper wire is replaced by the led and ben drops the magnet through the. The force (f) a magnetic field (b) exerts on an individual charge (q) traveling at drift velocity v d is: To investigate this force, let’s consider the. F = qvdb sin θ (21.5.3). Copper Wire Magnetic Force.
From www.youtube.com
vs Copper Wire Reaction YouTube Copper Wire Magnetic Force B = \frac {\mu_0 i} {2\pi d} b = 2πdμ0i. I i — current flowing. The force (f) a magnetic field (b) exerts on an individual charge (q) traveling at drift velocity v d is: When the connection in the copper wire is replaced by the led and ben drops the magnet through the. In this instance, θ represents the. Copper Wire Magnetic Force.
From www.youtube.com
Copper's Surprising Reaction to Strong Force Field Motion Copper Wire Magnetic Force The force (f) a magnetic field (b) exerts on an individual charge (q) traveling at drift velocity v d is: Wire losses of high frequency currents due to skin effects inside the wire which force high frequency current to flow on the outside surface of the. F = qvdb sin θ (21.5.3) (21.5.3) f = q v d b sin. Copper Wire Magnetic Force.
From www.youtube.com
Force on a Current Carrying Wire YouTube Copper Wire Magnetic Force To investigate this force, let’s consider the. Wire losses of high frequency currents due to skin effects inside the wire which force high frequency current to flow on the outside surface of the. B = \frac {\mu_0 i} {2\pi d} b = 2πdμ0i. Assuming that our wire is straight and very long, we can estimate a magnetic field around the. Copper Wire Magnetic Force.
From www.discoveryexpresskids.com
Fields of Attraction and Discovery Express Copper Wire Magnetic Force B = \frac {\mu_0 i} {2\pi d} b = 2πdμ0i. Assuming that our wire is straight and very long, we can estimate a magnetic field around the wire with the following equation: F = qvdb sin θ (21.5.3) (21.5.3) f = q v d b sin θ. In this instance, θ represents the angle between. Wire losses of high frequency. Copper Wire Magnetic Force.
From www.slideserve.com
PPT Chapter 27 Sources of the field PowerPoint Presentation Copper Wire Magnetic Force In this instance, θ represents the angle between. B = \frac {\mu_0 i} {2\pi d} b = 2πdμ0i. F = qvdb sin θ (21.5.3) (21.5.3) f = q v d b sin θ. I i — current flowing. When the connection in the copper wire is replaced by the led and ben drops the magnet through the. Wire losses of. Copper Wire Magnetic Force.
From sdsu-physics.org
Fields Copper Wire Magnetic Force When the connection in the copper wire is replaced by the led and ben drops the magnet through the. Wire losses of high frequency currents due to skin effects inside the wire which force high frequency current to flow on the outside surface of the. B = \frac {\mu_0 i} {2\pi d} b = 2πdμ0i. In this instance, θ represents. Copper Wire Magnetic Force.
From stoplearn.com
and its properties and Types, field and Copper Wire Magnetic Force Assuming that our wire is straight and very long, we can estimate a magnetic field around the wire with the following equation: Wire losses of high frequency currents due to skin effects inside the wire which force high frequency current to flow on the outside surface of the. The force (f) a magnetic field (b) exerts on an individual charge. Copper Wire Magnetic Force.
From www.alamy.com
field of a currentcarrying coil. coil Copper Wire Magnetic Force F = qvdb sin θ (21.5.3) (21.5.3) f = q v d b sin θ. When the connection in the copper wire is replaced by the led and ben drops the magnet through the. Assuming that our wire is straight and very long, we can estimate a magnetic field around the wire with the following equation: Wire losses of high. Copper Wire Magnetic Force.
From www.youtube.com
Free Energy Using With Copper Wire 100 YouTube Copper Wire Magnetic Force B = \frac {\mu_0 i} {2\pi d} b = 2πdμ0i. When the connection in the copper wire is replaced by the led and ben drops the magnet through the. In this instance, θ represents the angle between. To investigate this force, let’s consider the. The force (f) a magnetic field (b) exerts on an individual charge (q) traveling at drift. Copper Wire Magnetic Force.
From askfilo.com
A copper wire is held between the poles of a The current in the w.. Copper Wire Magnetic Force F = qvdb sin θ (21.5.3) (21.5.3) f = q v d b sin θ. B = \frac {\mu_0 i} {2\pi d} b = 2πdμ0i. Assuming that our wire is straight and very long, we can estimate a magnetic field around the wire with the following equation: When the connection in the copper wire is replaced by the led and. Copper Wire Magnetic Force.
From philschatz.com
Force on a CurrentCarrying Conductor · Physics Copper Wire Magnetic Force I i — current flowing. To investigate this force, let’s consider the. The force (f) a magnetic field (b) exerts on an individual charge (q) traveling at drift velocity v d is: Wire losses of high frequency currents due to skin effects inside the wire which force high frequency current to flow on the outside surface of the. B =. Copper Wire Magnetic Force.
From www.youtube.com
free energy experiment using copper wire and simple science Copper Wire Magnetic Force When the connection in the copper wire is replaced by the led and ben drops the magnet through the. The force (f) a magnetic field (b) exerts on an individual charge (q) traveling at drift velocity v d is: In this instance, θ represents the angle between. F = qvdb sin θ (21.5.3) (21.5.3) f = q v d b. Copper Wire Magnetic Force.
From www.flexiprep.com
Physics Class 12 NCERT Solutions Chapter 4 Moving Charges and Copper Wire Magnetic Force B = \frac {\mu_0 i} {2\pi d} b = 2πdμ0i. Assuming that our wire is straight and very long, we can estimate a magnetic field around the wire with the following equation: When the connection in the copper wire is replaced by the led and ben drops the magnet through the. F = qvdb sin θ (21.5.3) (21.5.3) f =. Copper Wire Magnetic Force.
From mmerevise.co.uk
Flux Density Questions and Revision MME Copper Wire Magnetic Force When the connection in the copper wire is replaced by the led and ben drops the magnet through the. F = qvdb sin θ (21.5.3) (21.5.3) f = q v d b sin θ. Assuming that our wire is straight and very long, we can estimate a magnetic field around the wire with the following equation: I i — current. Copper Wire Magnetic Force.
From www.youtube.com
Play With Field Demonstrations Simple Wire Coils (MF) YouTube Copper Wire Magnetic Force In this instance, θ represents the angle between. Wire losses of high frequency currents due to skin effects inside the wire which force high frequency current to flow on the outside surface of the. F = qvdb sin θ (21.5.3) (21.5.3) f = q v d b sin θ. To investigate this force, let’s consider the. I i — current. Copper Wire Magnetic Force.
From www.hanlin.com
AQA A Level Physics复习笔记7.8.1 Force on a CurrentCarrying Copper Wire Magnetic Force B = \frac {\mu_0 i} {2\pi d} b = 2πdμ0i. Assuming that our wire is straight and very long, we can estimate a magnetic field around the wire with the following equation: The force (f) a magnetic field (b) exerts on an individual charge (q) traveling at drift velocity v d is: I i — current flowing. Wire losses of. Copper Wire Magnetic Force.
From www.alamy.com
Coil wire field lines hires stock photography and images Alamy Copper Wire Magnetic Force In this instance, θ represents the angle between. Assuming that our wire is straight and very long, we can estimate a magnetic field around the wire with the following equation: To investigate this force, let’s consider the. I i — current flowing. Wire losses of high frequency currents due to skin effects inside the wire which force high frequency current. Copper Wire Magnetic Force.
From www.ultrafinecopperwire.com
Enameled Copper Wire Copper Wire Magnetic Force I i — current flowing. When the connection in the copper wire is replaced by the led and ben drops the magnet through the. To investigate this force, let’s consider the. B = \frac {\mu_0 i} {2\pi d} b = 2πdμ0i. F = qvdb sin θ (21.5.3) (21.5.3) f = q v d b sin θ. Wire losses of high. Copper Wire Magnetic Force.
From www.clearwaycommunitysolar.com
Make Your Own Clearway Community Solar Copper Wire Magnetic Force I i — current flowing. F = qvdb sin θ (21.5.3) (21.5.3) f = q v d b sin θ. When the connection in the copper wire is replaced by the led and ben drops the magnet through the. B = \frac {\mu_0 i} {2\pi d} b = 2πdμ0i. To investigate this force, let’s consider the. The force (f) a. Copper Wire Magnetic Force.