How To Get Tan From Sin And Cos Unit Circle . Learn how to define sine, cosine, and tangent for any angle using the unit circle, a circle of radius 1 centered at the origin. In the first and third quadrants, $\tan(\theta)$ is the length from $(\cos(\theta),\sin(\theta))$ to the $x$ axis along the line tangent to the circle at. Learn how to use the unit circle to find trigonometric functions of any angle. Follow the mnemonic devices of pizza, pies and square tables to. Because the radius is 1, we can directly measure sine, cosine and tangent. See how to graph the unit circle and use it to evaluate trigonometric. Learn how to find these values using the unit circle and other methods, with plenty of examples and. Enter the angle and get the coordinates of the point on. Sine, cosine and tangent (often shortened to sin, cos and tan) are each a ratio of sides of a right angled triangle: Learn how to use the unit circle to define trigonometric functions such as sine, cosine and tangent. For a given angle θ each ratio.
from thirdspacelearning.com
Learn how to find these values using the unit circle and other methods, with plenty of examples and. Learn how to use the unit circle to define trigonometric functions such as sine, cosine and tangent. See how to graph the unit circle and use it to evaluate trigonometric. For a given angle θ each ratio. Because the radius is 1, we can directly measure sine, cosine and tangent. Follow the mnemonic devices of pizza, pies and square tables to. Sine, cosine and tangent (often shortened to sin, cos and tan) are each a ratio of sides of a right angled triangle: Learn how to define sine, cosine, and tangent for any angle using the unit circle, a circle of radius 1 centered at the origin. Learn how to use the unit circle to find trigonometric functions of any angle. In the first and third quadrants, $\tan(\theta)$ is the length from $(\cos(\theta),\sin(\theta))$ to the $x$ axis along the line tangent to the circle at.
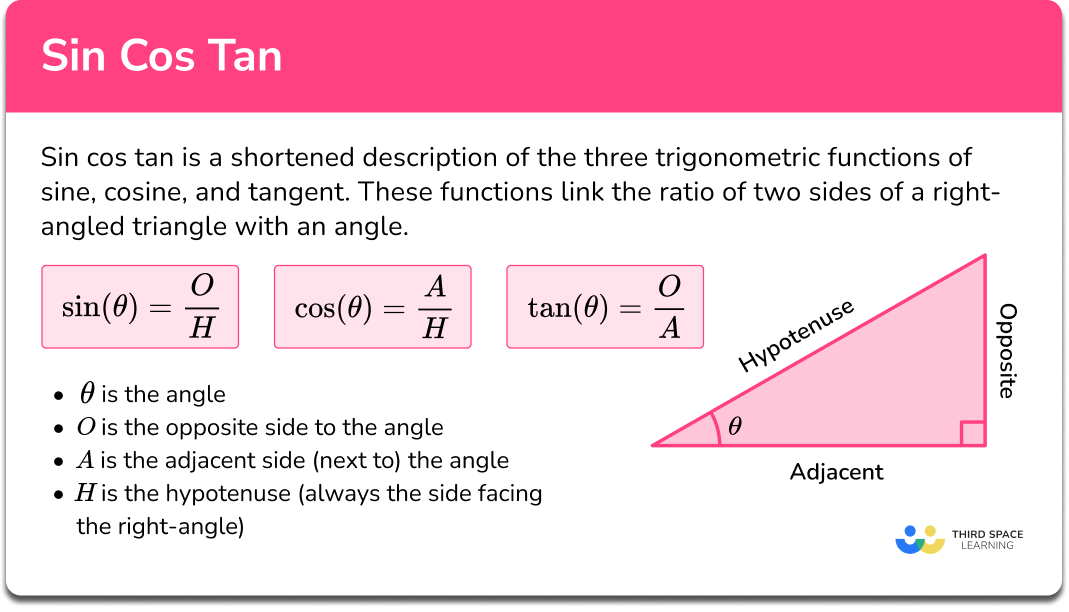
Sin Cos Tan GCSE Maths Steps, Examples & Worksheet
How To Get Tan From Sin And Cos Unit Circle Because the radius is 1, we can directly measure sine, cosine and tangent. Learn how to use the unit circle to define trigonometric functions such as sine, cosine and tangent. Sine, cosine and tangent (often shortened to sin, cos and tan) are each a ratio of sides of a right angled triangle: In the first and third quadrants, $\tan(\theta)$ is the length from $(\cos(\theta),\sin(\theta))$ to the $x$ axis along the line tangent to the circle at. For a given angle θ each ratio. Learn how to define sine, cosine, and tangent for any angle using the unit circle, a circle of radius 1 centered at the origin. See how to graph the unit circle and use it to evaluate trigonometric. Follow the mnemonic devices of pizza, pies and square tables to. Learn how to use the unit circle to find trigonometric functions of any angle. Learn how to find these values using the unit circle and other methods, with plenty of examples and. Because the radius is 1, we can directly measure sine, cosine and tangent. Enter the angle and get the coordinates of the point on.
From mavink.com
Unit Circle With Sin Cos Tan How To Get Tan From Sin And Cos Unit Circle Learn how to use the unit circle to define trigonometric functions such as sine, cosine and tangent. Sine, cosine and tangent (often shortened to sin, cos and tan) are each a ratio of sides of a right angled triangle: For a given angle θ each ratio. Because the radius is 1, we can directly measure sine, cosine and tangent. Learn. How To Get Tan From Sin And Cos Unit Circle.
From thirdspacelearning.com
Sin Cos Tan GCSE Maths Steps, Examples & Worksheet How To Get Tan From Sin And Cos Unit Circle Learn how to define sine, cosine, and tangent for any angle using the unit circle, a circle of radius 1 centered at the origin. See how to graph the unit circle and use it to evaluate trigonometric. Enter the angle and get the coordinates of the point on. Learn how to use the unit circle to define trigonometric functions such. How To Get Tan From Sin And Cos Unit Circle.
From mungfali.com
Unit Circle Sin Cos How To Get Tan From Sin And Cos Unit Circle For a given angle θ each ratio. Sine, cosine and tangent (often shortened to sin, cos and tan) are each a ratio of sides of a right angled triangle: Learn how to find these values using the unit circle and other methods, with plenty of examples and. Learn how to define sine, cosine, and tangent for any angle using the. How To Get Tan From Sin And Cos Unit Circle.
From srktflyahzgjsm.blogspot.com
How To Find Sin Cos Tan On Unit Circle We have already seen in the How To Get Tan From Sin And Cos Unit Circle Enter the angle and get the coordinates of the point on. For a given angle θ each ratio. In the first and third quadrants, $\tan(\theta)$ is the length from $(\cos(\theta),\sin(\theta))$ to the $x$ axis along the line tangent to the circle at. Learn how to define sine, cosine, and tangent for any angle using the unit circle, a circle of. How To Get Tan From Sin And Cos Unit Circle.
From www.youtube.com
Unit Circle Sin, Cos, Tan YouTube How To Get Tan From Sin And Cos Unit Circle Follow the mnemonic devices of pizza, pies and square tables to. For a given angle θ each ratio. Because the radius is 1, we can directly measure sine, cosine and tangent. Learn how to define sine, cosine, and tangent for any angle using the unit circle, a circle of radius 1 centered at the origin. Learn how to use the. How To Get Tan From Sin And Cos Unit Circle.
From www.babezdoor.com
Unit Circle Tangents Tim S Printables The Best Porn site How To Get Tan From Sin And Cos Unit Circle Because the radius is 1, we can directly measure sine, cosine and tangent. Sine, cosine and tangent (often shortened to sin, cos and tan) are each a ratio of sides of a right angled triangle: Learn how to find these values using the unit circle and other methods, with plenty of examples and. Enter the angle and get the coordinates. How To Get Tan From Sin And Cos Unit Circle.
From www.youtube.com
08 Calculate Sin, Cos & Tan w/ Unit Circle in Radians Part 1 YouTube How To Get Tan From Sin And Cos Unit Circle See how to graph the unit circle and use it to evaluate trigonometric. Learn how to define sine, cosine, and tangent for any angle using the unit circle, a circle of radius 1 centered at the origin. In the first and third quadrants, $\tan(\theta)$ is the length from $(\cos(\theta),\sin(\theta))$ to the $x$ axis along the line tangent to the circle. How To Get Tan From Sin And Cos Unit Circle.
From www.youtube.com
Trigonometric Functions on the Unit Circle to define sine, cosine YouTube How To Get Tan From Sin And Cos Unit Circle See how to graph the unit circle and use it to evaluate trigonometric. Follow the mnemonic devices of pizza, pies and square tables to. In the first and third quadrants, $\tan(\theta)$ is the length from $(\cos(\theta),\sin(\theta))$ to the $x$ axis along the line tangent to the circle at. Learn how to use the unit circle to define trigonometric functions such. How To Get Tan From Sin And Cos Unit Circle.
From www.geeksforgeeks.org
How to use the Unit Circle in Trigonometry? How To Get Tan From Sin And Cos Unit Circle Follow the mnemonic devices of pizza, pies and square tables to. In the first and third quadrants, $\tan(\theta)$ is the length from $(\cos(\theta),\sin(\theta))$ to the $x$ axis along the line tangent to the circle at. Sine, cosine and tangent (often shortened to sin, cos and tan) are each a ratio of sides of a right angled triangle: Learn how to. How To Get Tan From Sin And Cos Unit Circle.
From byjus.com
Tan 30 Degrees Value (Unit Circle Tangent Value) How To Get Tan From Sin And Cos Unit Circle Sine, cosine and tangent (often shortened to sin, cos and tan) are each a ratio of sides of a right angled triangle: In the first and third quadrants, $\tan(\theta)$ is the length from $(\cos(\theta),\sin(\theta))$ to the $x$ axis along the line tangent to the circle at. Learn how to use the unit circle to define trigonometric functions such as sine,. How To Get Tan From Sin And Cos Unit Circle.
From firmfunda.com
Trigonometry (advanced) Trigonometric Values Unit Circle Form How To Get Tan From Sin And Cos Unit Circle Learn how to define sine, cosine, and tangent for any angle using the unit circle, a circle of radius 1 centered at the origin. Learn how to find these values using the unit circle and other methods, with plenty of examples and. In the first and third quadrants, $\tan(\theta)$ is the length from $(\cos(\theta),\sin(\theta))$ to the $x$ axis along the. How To Get Tan From Sin And Cos Unit Circle.
From www.youtube.com
The Unit Circle, Sin, Cos and Tan YouTube How To Get Tan From Sin And Cos Unit Circle For a given angle θ each ratio. Learn how to find these values using the unit circle and other methods, with plenty of examples and. Follow the mnemonic devices of pizza, pies and square tables to. See how to graph the unit circle and use it to evaluate trigonometric. Learn how to define sine, cosine, and tangent for any angle. How To Get Tan From Sin And Cos Unit Circle.
From www.cuemath.com
Unit circle Trigonometric Functions using Unit Circle Unit Circle How To Get Tan From Sin And Cos Unit Circle Learn how to use the unit circle to find trigonometric functions of any angle. Follow the mnemonic devices of pizza, pies and square tables to. In the first and third quadrants, $\tan(\theta)$ is the length from $(\cos(\theta),\sin(\theta))$ to the $x$ axis along the line tangent to the circle at. Because the radius is 1, we can directly measure sine, cosine. How To Get Tan From Sin And Cos Unit Circle.
From beta.geogebra.org
The unit circle and sin, cos and tan functions GeoGebra How To Get Tan From Sin And Cos Unit Circle Follow the mnemonic devices of pizza, pies and square tables to. For a given angle θ each ratio. Enter the angle and get the coordinates of the point on. Learn how to define sine, cosine, and tangent for any angle using the unit circle, a circle of radius 1 centered at the origin. See how to graph the unit circle. How To Get Tan From Sin And Cos Unit Circle.
From mungfali.com
Trigonometry Unit Circle Chart How To Get Tan From Sin And Cos Unit Circle For a given angle θ each ratio. Because the radius is 1, we can directly measure sine, cosine and tangent. Enter the angle and get the coordinates of the point on. Learn how to use the unit circle to find trigonometric functions of any angle. Learn how to define sine, cosine, and tangent for any angle using the unit circle,. How To Get Tan From Sin And Cos Unit Circle.
From www.sampletemplates.com
FREE 6+ Sin Cos Tan Chart Templates in PDF How To Get Tan From Sin And Cos Unit Circle See how to graph the unit circle and use it to evaluate trigonometric. Learn how to use the unit circle to define trigonometric functions such as sine, cosine and tangent. Enter the angle and get the coordinates of the point on. Learn how to use the unit circle to find trigonometric functions of any angle. Because the radius is 1,. How To Get Tan From Sin And Cos Unit Circle.
From www.youtube.com
Exact Values of Sin, Cos & Tan from Unit Circle YouTube How To Get Tan From Sin And Cos Unit Circle In the first and third quadrants, $\tan(\theta)$ is the length from $(\cos(\theta),\sin(\theta))$ to the $x$ axis along the line tangent to the circle at. For a given angle θ each ratio. Learn how to define sine, cosine, and tangent for any angle using the unit circle, a circle of radius 1 centered at the origin. Follow the mnemonic devices of. How To Get Tan From Sin And Cos Unit Circle.
From wiki.math.ucr.edu
Unit Circle Essential Trigonometric Values Math Wiki How To Get Tan From Sin And Cos Unit Circle Sine, cosine and tangent (often shortened to sin, cos and tan) are each a ratio of sides of a right angled triangle: Because the radius is 1, we can directly measure sine, cosine and tangent. Learn how to find these values using the unit circle and other methods, with plenty of examples and. Enter the angle and get the coordinates. How To Get Tan From Sin And Cos Unit Circle.
From matterofmath.com
Unit Circle Quick Lesson Printable PDF Chart · Matter of Math How To Get Tan From Sin And Cos Unit Circle See how to graph the unit circle and use it to evaluate trigonometric. Enter the angle and get the coordinates of the point on. Because the radius is 1, we can directly measure sine, cosine and tangent. In the first and third quadrants, $\tan(\theta)$ is the length from $(\cos(\theta),\sin(\theta))$ to the $x$ axis along the line tangent to the circle. How To Get Tan From Sin And Cos Unit Circle.
From mungfali.com
Trigonometry Formulas Sin Cos Tan How To Get Tan From Sin And Cos Unit Circle Learn how to define sine, cosine, and tangent for any angle using the unit circle, a circle of radius 1 centered at the origin. Sine, cosine and tangent (often shortened to sin, cos and tan) are each a ratio of sides of a right angled triangle: Learn how to find these values using the unit circle and other methods, with. How To Get Tan From Sin And Cos Unit Circle.
From demonstrations.wolfram.com
Relationship of Sine and Cosine to the Unit Circle Wolfram How To Get Tan From Sin And Cos Unit Circle In the first and third quadrants, $\tan(\theta)$ is the length from $(\cos(\theta),\sin(\theta))$ to the $x$ axis along the line tangent to the circle at. Because the radius is 1, we can directly measure sine, cosine and tangent. Sine, cosine and tangent (often shortened to sin, cos and tan) are each a ratio of sides of a right angled triangle: Learn. How To Get Tan From Sin And Cos Unit Circle.
From mungfali.com
Sin Cos Tan Circle How To Get Tan From Sin And Cos Unit Circle Learn how to find these values using the unit circle and other methods, with plenty of examples and. Learn how to use the unit circle to define trigonometric functions such as sine, cosine and tangent. Follow the mnemonic devices of pizza, pies and square tables to. Enter the angle and get the coordinates of the point on. See how to. How To Get Tan From Sin And Cos Unit Circle.
From crystalclearmaths.com
The Unit Circle and Trigonometric Identities Crystal Clear Mathematics How To Get Tan From Sin And Cos Unit Circle Learn how to find these values using the unit circle and other methods, with plenty of examples and. Sine, cosine and tangent (often shortened to sin, cos and tan) are each a ratio of sides of a right angled triangle: For a given angle θ each ratio. Learn how to use the unit circle to find trigonometric functions of any. How To Get Tan From Sin And Cos Unit Circle.
From printable.mist-bd.org
Printable Unit Circle How To Get Tan From Sin And Cos Unit Circle Because the radius is 1, we can directly measure sine, cosine and tangent. In the first and third quadrants, $\tan(\theta)$ is the length from $(\cos(\theta),\sin(\theta))$ to the $x$ axis along the line tangent to the circle at. Learn how to define sine, cosine, and tangent for any angle using the unit circle, a circle of radius 1 centered at the. How To Get Tan From Sin And Cos Unit Circle.
From www.youtube.com
Finding Sine and Cosine Values from a Unit Circle YouTube How To Get Tan From Sin And Cos Unit Circle Learn how to use the unit circle to find trigonometric functions of any angle. Follow the mnemonic devices of pizza, pies and square tables to. Learn how to find these values using the unit circle and other methods, with plenty of examples and. For a given angle θ each ratio. Enter the angle and get the coordinates of the point. How To Get Tan From Sin And Cos Unit Circle.
From www.houseofmath.com
How Does the Unit Circle Work? House of Math How To Get Tan From Sin And Cos Unit Circle Learn how to define sine, cosine, and tangent for any angle using the unit circle, a circle of radius 1 centered at the origin. For a given angle θ each ratio. In the first and third quadrants, $\tan(\theta)$ is the length from $(\cos(\theta),\sin(\theta))$ to the $x$ axis along the line tangent to the circle at. Follow the mnemonic devices of. How To Get Tan From Sin And Cos Unit Circle.
From ck12.org
Unit Circle ( Read ) Trigonometry CK12 Foundation How To Get Tan From Sin And Cos Unit Circle Enter the angle and get the coordinates of the point on. Learn how to use the unit circle to find trigonometric functions of any angle. Sine, cosine and tangent (often shortened to sin, cos and tan) are each a ratio of sides of a right angled triangle: Learn how to define sine, cosine, and tangent for any angle using the. How To Get Tan From Sin And Cos Unit Circle.
From www.geeksforgeeks.org
How to use the Unit Circle in Trigonometry? How To Get Tan From Sin And Cos Unit Circle Sine, cosine and tangent (often shortened to sin, cos and tan) are each a ratio of sides of a right angled triangle: See how to graph the unit circle and use it to evaluate trigonometric. Learn how to find these values using the unit circle and other methods, with plenty of examples and. In the first and third quadrants, $\tan(\theta)$. How To Get Tan From Sin And Cos Unit Circle.
From www.youtube.com
sin, cos, and tan for Standard Unit Circle Angles YouTube How To Get Tan From Sin And Cos Unit Circle Learn how to use the unit circle to find trigonometric functions of any angle. See how to graph the unit circle and use it to evaluate trigonometric. Follow the mnemonic devices of pizza, pies and square tables to. For a given angle θ each ratio. Because the radius is 1, we can directly measure sine, cosine and tangent. In the. How To Get Tan From Sin And Cos Unit Circle.
From www.youtube.com
Trig Unit Circle Filling in Sine, Cos and Tan YouTube How To Get Tan From Sin And Cos Unit Circle Because the radius is 1, we can directly measure sine, cosine and tangent. Learn how to define sine, cosine, and tangent for any angle using the unit circle, a circle of radius 1 centered at the origin. Follow the mnemonic devices of pizza, pies and square tables to. See how to graph the unit circle and use it to evaluate. How To Get Tan From Sin And Cos Unit Circle.
From mycours.es
p5 Trigonometric functions and oscillation (sin, cos) EMS Interactivity How To Get Tan From Sin And Cos Unit Circle For a given angle θ each ratio. Learn how to define sine, cosine, and tangent for any angle using the unit circle, a circle of radius 1 centered at the origin. Follow the mnemonic devices of pizza, pies and square tables to. In the first and third quadrants, $\tan(\theta)$ is the length from $(\cos(\theta),\sin(\theta))$ to the $x$ axis along the. How To Get Tan From Sin And Cos Unit Circle.
From www.teachoo.com
Trigonometry Formulas and Identities Full list Teachoo How To Get Tan From Sin And Cos Unit Circle Learn how to use the unit circle to find trigonometric functions of any angle. Learn how to use the unit circle to define trigonometric functions such as sine, cosine and tangent. Because the radius is 1, we can directly measure sine, cosine and tangent. Learn how to define sine, cosine, and tangent for any angle using the unit circle, a. How To Get Tan From Sin And Cos Unit Circle.
From owlcation.com
Trigonometry Graphing the Sine, Cosine and Tangent Functions Owlcation How To Get Tan From Sin And Cos Unit Circle Enter the angle and get the coordinates of the point on. Learn how to find these values using the unit circle and other methods, with plenty of examples and. Sine, cosine and tangent (often shortened to sin, cos and tan) are each a ratio of sides of a right angled triangle: See how to graph the unit circle and use. How To Get Tan From Sin And Cos Unit Circle.
From science.howstuffworks.com
How to Use the Unit Circle in Trigonometry HowStuffWorks How To Get Tan From Sin And Cos Unit Circle Learn how to use the unit circle to define trigonometric functions such as sine, cosine and tangent. See how to graph the unit circle and use it to evaluate trigonometric. Learn how to use the unit circle to find trigonometric functions of any angle. Because the radius is 1, we can directly measure sine, cosine and tangent. In the first. How To Get Tan From Sin And Cos Unit Circle.
From www.cuemath.com
Unit Circle With Tangent Values, Chart, Calculator How To Get Tan From Sin And Cos Unit Circle Sine, cosine and tangent (often shortened to sin, cos and tan) are each a ratio of sides of a right angled triangle: See how to graph the unit circle and use it to evaluate trigonometric. Learn how to use the unit circle to define trigonometric functions such as sine, cosine and tangent. Follow the mnemonic devices of pizza, pies and. How To Get Tan From Sin And Cos Unit Circle.