Cot X Over Csc X . We can also divide the other way around (such as adjacent/opposite instead of opposite/adjacent) to get: Rewrite csc(x) csc (x) in terms of sines and cosines. Cscx cotx = cscxtanx = 1 sinx sinx cosx = 1 cosx = secx. The remaining trigonometric functions secant (sec), cosecant (csc), and cotangent (cot) are defined as the reciprocal functions of cosine, sine, and tangent, respectively. Multiply by the reciprocal of the fraction to divide. Rewrite cot(x) cot (x) in terms of sines and cosines. Csc (θ) = hypotenuse /. = cosx sinx 1 sinx ⇐ use cotx = cosx sinx instead of 1 tanx. Csc x over cot x? Each of the six trig. Substitute your reciprocal and quotient identities into the equation: We know that cscx = 1 sinx, cotx = 1 tanx, tanx = sinx cosx.
from www.adda247.com
Cscx cotx = cscxtanx = 1 sinx sinx cosx = 1 cosx = secx. Csc (θ) = hypotenuse /. Rewrite cot(x) cot (x) in terms of sines and cosines. Csc x over cot x? We know that cscx = 1 sinx, cotx = 1 tanx, tanx = sinx cosx. The remaining trigonometric functions secant (sec), cosecant (csc), and cotangent (cot) are defined as the reciprocal functions of cosine, sine, and tangent, respectively. Substitute your reciprocal and quotient identities into the equation: Each of the six trig. Multiply by the reciprocal of the fraction to divide. = cosx sinx 1 sinx ⇐ use cotx = cosx sinx instead of 1 tanx.
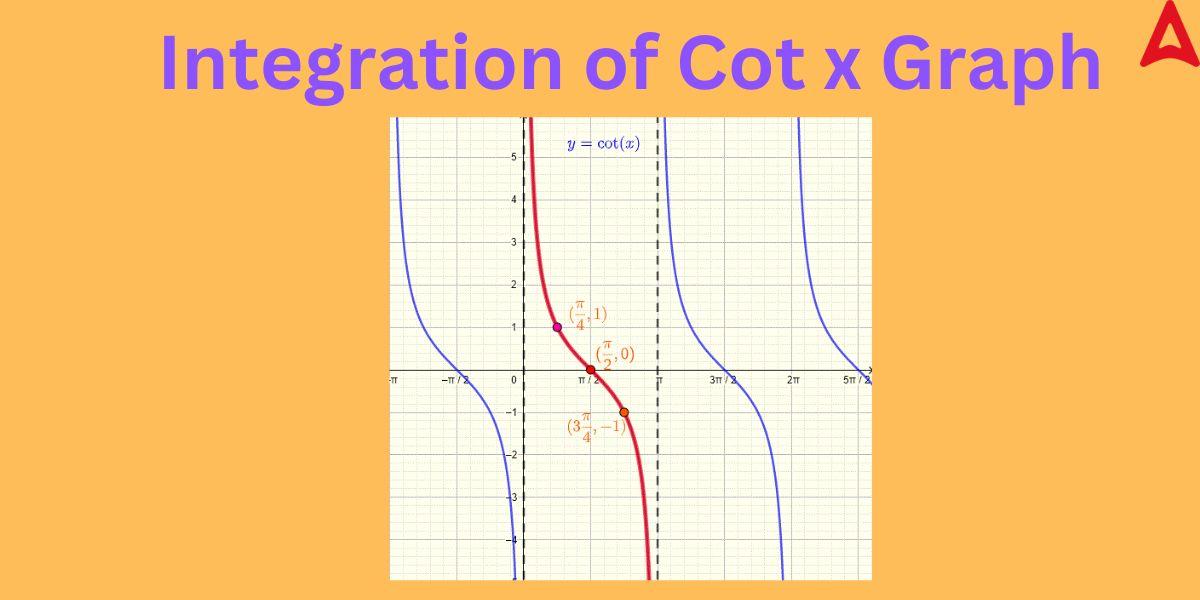
Integration of Cot x Explanation, Formula, Derivation, Examples
Cot X Over Csc X Each of the six trig. Each of the six trig. Csc x over cot x? Multiply by the reciprocal of the fraction to divide. Csc (θ) = hypotenuse /. Cscx cotx = cscxtanx = 1 sinx sinx cosx = 1 cosx = secx. Substitute your reciprocal and quotient identities into the equation: We know that cscx = 1 sinx, cotx = 1 tanx, tanx = sinx cosx. = cosx sinx 1 sinx ⇐ use cotx = cosx sinx instead of 1 tanx. Rewrite cot(x) cot (x) in terms of sines and cosines. We can also divide the other way around (such as adjacent/opposite instead of opposite/adjacent) to get: Rewrite csc(x) csc (x) in terms of sines and cosines. The remaining trigonometric functions secant (sec), cosecant (csc), and cotangent (cot) are defined as the reciprocal functions of cosine, sine, and tangent, respectively.
From www.epsilonify.com
What is the integral of csc(x)? Epsilonify Cot X Over Csc X Csc (θ) = hypotenuse /. Rewrite csc(x) csc (x) in terms of sines and cosines. Multiply by the reciprocal of the fraction to divide. Cscx cotx = cscxtanx = 1 sinx sinx cosx = 1 cosx = secx. Rewrite cot(x) cot (x) in terms of sines and cosines. The remaining trigonometric functions secant (sec), cosecant (csc), and cotangent (cot) are. Cot X Over Csc X.
From www.numerade.com
SOLVED Simplify the trigonometric expression below by writing the Cot X Over Csc X Multiply by the reciprocal of the fraction to divide. We know that cscx = 1 sinx, cotx = 1 tanx, tanx = sinx cosx. The remaining trigonometric functions secant (sec), cosecant (csc), and cotangent (cot) are defined as the reciprocal functions of cosine, sine, and tangent, respectively. Rewrite csc(x) csc (x) in terms of sines and cosines. We can also. Cot X Over Csc X.
From solvedlib.com
Prove that(csc(x))csc(x) cot(x)(csc(X))Jro) sin?(x)si… SolvedLib Cot X Over Csc X Substitute your reciprocal and quotient identities into the equation: The remaining trigonometric functions secant (sec), cosecant (csc), and cotangent (cot) are defined as the reciprocal functions of cosine, sine, and tangent, respectively. We know that cscx = 1 sinx, cotx = 1 tanx, tanx = sinx cosx. We can also divide the other way around (such as adjacent/opposite instead of. Cot X Over Csc X.
From solvedlib.com
Prove that d (csc(x)) dxcsc(x) cot(x){(csc(x)) dxaXJr… SolvedLib Cot X Over Csc X Multiply by the reciprocal of the fraction to divide. Rewrite cot(x) cot (x) in terms of sines and cosines. The remaining trigonometric functions secant (sec), cosecant (csc), and cotangent (cot) are defined as the reciprocal functions of cosine, sine, and tangent, respectively. Each of the six trig. We can also divide the other way around (such as adjacent/opposite instead of. Cot X Over Csc X.
From www.youtube.com
Verify Trig Identity (csc x 1)/ cot x = cot x/(csc x +1). Multiply by Cot X Over Csc X Each of the six trig. Rewrite cot(x) cot (x) in terms of sines and cosines. Cscx cotx = cscxtanx = 1 sinx sinx cosx = 1 cosx = secx. We can also divide the other way around (such as adjacent/opposite instead of opposite/adjacent) to get: Substitute your reciprocal and quotient identities into the equation: = cosx sinx 1 sinx ⇐. Cot X Over Csc X.
From www.coursehero.com
[Solved] Prove the following identities cscx + cotx sec x tan x sec Cot X Over Csc X We know that cscx = 1 sinx, cotx = 1 tanx, tanx = sinx cosx. Csc (θ) = hypotenuse /. = cosx sinx 1 sinx ⇐ use cotx = cosx sinx instead of 1 tanx. Csc x over cot x? Cscx cotx = cscxtanx = 1 sinx sinx cosx = 1 cosx = secx. Rewrite cot(x) cot (x) in terms. Cot X Over Csc X.
From www.youtube.com
Verify 1/(1 cos x) 1/(1 + cos x) = 2 cot x csc x YouTube Cot X Over Csc X Multiply by the reciprocal of the fraction to divide. Each of the six trig. Rewrite cot(x) cot (x) in terms of sines and cosines. Cscx cotx = cscxtanx = 1 sinx sinx cosx = 1 cosx = secx. = cosx sinx 1 sinx ⇐ use cotx = cosx sinx instead of 1 tanx. Substitute your reciprocal and quotient identities into. Cot X Over Csc X.
From www.chegg.com
Solved ) sin x+cos x cot x =csc X EL GREEN Formulas and Cot X Over Csc X Multiply by the reciprocal of the fraction to divide. We can also divide the other way around (such as adjacent/opposite instead of opposite/adjacent) to get: Substitute your reciprocal and quotient identities into the equation: Csc x over cot x? We know that cscx = 1 sinx, cotx = 1 tanx, tanx = sinx cosx. Cscx cotx = cscxtanx = 1. Cot X Over Csc X.
From mungfali.com
Sin Cos Tan CSC Cot X Over Csc X = cosx sinx 1 sinx ⇐ use cotx = cosx sinx instead of 1 tanx. Rewrite csc(x) csc (x) in terms of sines and cosines. We know that cscx = 1 sinx, cotx = 1 tanx, tanx = sinx cosx. Cscx cotx = cscxtanx = 1 sinx sinx cosx = 1 cosx = secx. We can also divide the other. Cot X Over Csc X.
From socratic.org
How do you express cosθ csc θ in terms of tanθ? Socratic Cot X Over Csc X = cosx sinx 1 sinx ⇐ use cotx = cosx sinx instead of 1 tanx. Csc x over cot x? Rewrite csc(x) csc (x) in terms of sines and cosines. Each of the six trig. We can also divide the other way around (such as adjacent/opposite instead of opposite/adjacent) to get: Multiply by the reciprocal of the fraction to divide.. Cot X Over Csc X.
From www.youtube.com
Integration Formulas for 1/x, tan(x), cot(x), sec(x), csc(x) YouTube Cot X Over Csc X We know that cscx = 1 sinx, cotx = 1 tanx, tanx = sinx cosx. Rewrite cot(x) cot (x) in terms of sines and cosines. Rewrite csc(x) csc (x) in terms of sines and cosines. Csc x over cot x? Csc (θ) = hypotenuse /. Substitute your reciprocal and quotient identities into the equation: Multiply by the reciprocal of the. Cot X Over Csc X.
From www.youtube.com
derivative of ln(csc(x)cot(x)) YouTube Cot X Over Csc X We can also divide the other way around (such as adjacent/opposite instead of opposite/adjacent) to get: We know that cscx = 1 sinx, cotx = 1 tanx, tanx = sinx cosx. Rewrite csc(x) csc (x) in terms of sines and cosines. Substitute your reciprocal and quotient identities into the equation: Multiply by the reciprocal of the fraction to divide. =. Cot X Over Csc X.
From loecjmkyv.blob.core.windows.net
Given Csc X Cot X Sqrt 2 at Arlene Baker blog Cot X Over Csc X Rewrite csc(x) csc (x) in terms of sines and cosines. Each of the six trig. Multiply by the reciprocal of the fraction to divide. Csc (θ) = hypotenuse /. We know that cscx = 1 sinx, cotx = 1 tanx, tanx = sinx cosx. We can also divide the other way around (such as adjacent/opposite instead of opposite/adjacent) to get:. Cot X Over Csc X.
From www.youtube.com
sen x/cos x + tan x/cot x + sec x/csc x=2cot x+1/cot2 x YouTube Cot X Over Csc X = cosx sinx 1 sinx ⇐ use cotx = cosx sinx instead of 1 tanx. Rewrite csc(x) csc (x) in terms of sines and cosines. Substitute your reciprocal and quotient identities into the equation: We can also divide the other way around (such as adjacent/opposite instead of opposite/adjacent) to get: Rewrite cot(x) cot (x) in terms of sines and cosines.. Cot X Over Csc X.
From www.youtube.com
Reciprocal Trigonometric Functions (Cosecant, Secant, Cotangent) YouTube Cot X Over Csc X We can also divide the other way around (such as adjacent/opposite instead of opposite/adjacent) to get: We know that cscx = 1 sinx, cotx = 1 tanx, tanx = sinx cosx. Rewrite cot(x) cot (x) in terms of sines and cosines. Substitute your reciprocal and quotient identities into the equation: Csc x over cot x? Rewrite csc(x) csc (x) in. Cot X Over Csc X.
From www.youtube.com
Verify the Trig Identity (1 + cos(x))/sin(x) = csc(x) + cot(x) YouTube Cot X Over Csc X Cscx cotx = cscxtanx = 1 sinx sinx cosx = 1 cosx = secx. Substitute your reciprocal and quotient identities into the equation: Multiply by the reciprocal of the fraction to divide. We can also divide the other way around (such as adjacent/opposite instead of opposite/adjacent) to get: The remaining trigonometric functions secant (sec), cosecant (csc), and cotangent (cot) are. Cot X Over Csc X.
From www.youtube.com
Verify Identity cot x/(1+csc x)+(1+csc x))/cot x=2sec x Using Cot X Over Csc X Substitute your reciprocal and quotient identities into the equation: Each of the six trig. Multiply by the reciprocal of the fraction to divide. Rewrite csc(x) csc (x) in terms of sines and cosines. Cscx cotx = cscxtanx = 1 sinx sinx cosx = 1 cosx = secx. Csc (θ) = hypotenuse /. Csc x over cot x? We can also. Cot X Over Csc X.
From www.coursehero.com
[Solved] Verify that the equation is an identity. csc x sin x = cos x Cot X Over Csc X Rewrite cot(x) cot (x) in terms of sines and cosines. Rewrite csc(x) csc (x) in terms of sines and cosines. Substitute your reciprocal and quotient identities into the equation: = cosx sinx 1 sinx ⇐ use cotx = cosx sinx instead of 1 tanx. We can also divide the other way around (such as adjacent/opposite instead of opposite/adjacent) to get:. Cot X Over Csc X.
From www.numerade.com
SOLVED 'CSC X + COS X cot(x)' Cot X Over Csc X We can also divide the other way around (such as adjacent/opposite instead of opposite/adjacent) to get: We know that cscx = 1 sinx, cotx = 1 tanx, tanx = sinx cosx. Each of the six trig. Substitute your reciprocal and quotient identities into the equation: Cscx cotx = cscxtanx = 1 sinx sinx cosx = 1 cosx = secx. Multiply. Cot X Over Csc X.
From loecjmkyv.blob.core.windows.net
Given Csc X Cot X Sqrt 2 at Arlene Baker blog Cot X Over Csc X Cscx cotx = cscxtanx = 1 sinx sinx cosx = 1 cosx = secx. The remaining trigonometric functions secant (sec), cosecant (csc), and cotangent (cot) are defined as the reciprocal functions of cosine, sine, and tangent, respectively. Multiply by the reciprocal of the fraction to divide. We know that cscx = 1 sinx, cotx = 1 tanx, tanx = sinx. Cot X Over Csc X.
From www.teachoo.com
Ex 12.1, 21 Find lim x > 0 (cosec x cot x) Teachoo Cot X Over Csc X Each of the six trig. Cscx cotx = cscxtanx = 1 sinx sinx cosx = 1 cosx = secx. We can also divide the other way around (such as adjacent/opposite instead of opposite/adjacent) to get: Csc (θ) = hypotenuse /. Rewrite cot(x) cot (x) in terms of sines and cosines. Substitute your reciprocal and quotient identities into the equation: The. Cot X Over Csc X.
From www.youtube.com
Verifying a Trigonometric Identity cot(x)/csc(x) = cos(x) YouTube Cot X Over Csc X = cosx sinx 1 sinx ⇐ use cotx = cosx sinx instead of 1 tanx. Csc (θ) = hypotenuse /. Each of the six trig. Multiply by the reciprocal of the fraction to divide. Rewrite csc(x) csc (x) in terms of sines and cosines. Cscx cotx = cscxtanx = 1 sinx sinx cosx = 1 cosx = secx. Csc x. Cot X Over Csc X.
From www.numerade.com
SOLVED For the following exercises, simplify the first trigonometric Cot X Over Csc X = cosx sinx 1 sinx ⇐ use cotx = cosx sinx instead of 1 tanx. Multiply by the reciprocal of the fraction to divide. Rewrite cot(x) cot (x) in terms of sines and cosines. Each of the six trig. Csc (θ) = hypotenuse /. Csc x over cot x? We can also divide the other way around (such as adjacent/opposite. Cot X Over Csc X.
From www.numerade.com
Simplify the expression. sinx(tan x K cotx) sec X cOS X CSC X cot X Cot X Over Csc X Substitute your reciprocal and quotient identities into the equation: Each of the six trig. Rewrite cot(x) cot (x) in terms of sines and cosines. Csc (θ) = hypotenuse /. We can also divide the other way around (such as adjacent/opposite instead of opposite/adjacent) to get: Cscx cotx = cscxtanx = 1 sinx sinx cosx = 1 cosx = secx. The. Cot X Over Csc X.
From www.youtube.com
Csc, Sec, Cot Intro to Trigonometry YouTube Cot X Over Csc X Csc x over cot x? Rewrite csc(x) csc (x) in terms of sines and cosines. Rewrite cot(x) cot (x) in terms of sines and cosines. Substitute your reciprocal and quotient identities into the equation: We can also divide the other way around (such as adjacent/opposite instead of opposite/adjacent) to get: The remaining trigonometric functions secant (sec), cosecant (csc), and cotangent. Cot X Over Csc X.
From www.cuemath.com
Cosecant Secant And Cotangent Functions Solved Examples Cot X Over Csc X Csc x over cot x? Substitute your reciprocal and quotient identities into the equation: Multiply by the reciprocal of the fraction to divide. We know that cscx = 1 sinx, cotx = 1 tanx, tanx = sinx cosx. Cscx cotx = cscxtanx = 1 sinx sinx cosx = 1 cosx = secx. = cosx sinx 1 sinx ⇐ use cotx. Cot X Over Csc X.
From www.youtube.com
How to find the six Trigonometric Functions Sin, Cos, Tan, Cot, Sec Cot X Over Csc X Cscx cotx = cscxtanx = 1 sinx sinx cosx = 1 cosx = secx. Csc x over cot x? Csc (θ) = hypotenuse /. We know that cscx = 1 sinx, cotx = 1 tanx, tanx = sinx cosx. The remaining trigonometric functions secant (sec), cosecant (csc), and cotangent (cot) are defined as the reciprocal functions of cosine, sine, and. Cot X Over Csc X.
From www.teachoo.com
Example 3 (ii) Find the integral ∫ cosec x (cosec x + cot x) dx Cot X Over Csc X Each of the six trig. The remaining trigonometric functions secant (sec), cosecant (csc), and cotangent (cot) are defined as the reciprocal functions of cosine, sine, and tangent, respectively. Rewrite cot(x) cot (x) in terms of sines and cosines. Substitute your reciprocal and quotient identities into the equation: We know that cscx = 1 sinx, cotx = 1 tanx, tanx =. Cot X Over Csc X.
From www.chegg.com
Solved Verify the identity ♡ csc?x cotax CSC X+ cotx = CSC Cot X Over Csc X Rewrite cot(x) cot (x) in terms of sines and cosines. Rewrite csc(x) csc (x) in terms of sines and cosines. Cscx cotx = cscxtanx = 1 sinx sinx cosx = 1 cosx = secx. Csc (θ) = hypotenuse /. Each of the six trig. Substitute your reciprocal and quotient identities into the equation: Csc x over cot x? We can. Cot X Over Csc X.
From www.youtube.com
limit of csc(x)cot(x) as x goes to 0 via L'Hospital's rule YouTube Cot X Over Csc X Csc x over cot x? Rewrite cot(x) cot (x) in terms of sines and cosines. We can also divide the other way around (such as adjacent/opposite instead of opposite/adjacent) to get: = cosx sinx 1 sinx ⇐ use cotx = cosx sinx instead of 1 tanx. Csc (θ) = hypotenuse /. Multiply by the reciprocal of the fraction to divide.. Cot X Over Csc X.
From www.adda247.com
Integration of Cot x Explanation, Formula, Derivation, Examples Cot X Over Csc X Multiply by the reciprocal of the fraction to divide. Csc (θ) = hypotenuse /. Each of the six trig. We can also divide the other way around (such as adjacent/opposite instead of opposite/adjacent) to get: Rewrite cot(x) cot (x) in terms of sines and cosines. We know that cscx = 1 sinx, cotx = 1 tanx, tanx = sinx cosx.. Cot X Over Csc X.
From brainly.com
100 POINTS + BRAINLIEST PLEASE HELP!!!! Students were asked to prove Cot X Over Csc X Csc (θ) = hypotenuse /. = cosx sinx 1 sinx ⇐ use cotx = cosx sinx instead of 1 tanx. Each of the six trig. Multiply by the reciprocal of the fraction to divide. Substitute your reciprocal and quotient identities into the equation: Rewrite cot(x) cot (x) in terms of sines and cosines. Rewrite csc(x) csc (x) in terms of. Cot X Over Csc X.
From www.youtube.com
Integral of x*csc(x)*cot(x) Integral example YouTube Cot X Over Csc X = cosx sinx 1 sinx ⇐ use cotx = cosx sinx instead of 1 tanx. We can also divide the other way around (such as adjacent/opposite instead of opposite/adjacent) to get: Multiply by the reciprocal of the fraction to divide. Csc (θ) = hypotenuse /. Each of the six trig. Cscx cotx = cscxtanx = 1 sinx sinx cosx =. Cot X Over Csc X.
From www.youtube.com
Verify Trig Identity (tan x + cot x)/(sec x csc x) = 1. In terms of Cot X Over Csc X Csc x over cot x? We know that cscx = 1 sinx, cotx = 1 tanx, tanx = sinx cosx. Rewrite csc(x) csc (x) in terms of sines and cosines. Csc (θ) = hypotenuse /. Substitute your reciprocal and quotient identities into the equation: The remaining trigonometric functions secant (sec), cosecant (csc), and cotangent (cot) are defined as the reciprocal. Cot X Over Csc X.
From www.youtube.com
Integral of csc(x)*(cot(x) csc(x)) YouTube Cot X Over Csc X Cscx cotx = cscxtanx = 1 sinx sinx cosx = 1 cosx = secx. Csc x over cot x? Each of the six trig. = cosx sinx 1 sinx ⇐ use cotx = cosx sinx instead of 1 tanx. We know that cscx = 1 sinx, cotx = 1 tanx, tanx = sinx cosx. The remaining trigonometric functions secant (sec),. Cot X Over Csc X.