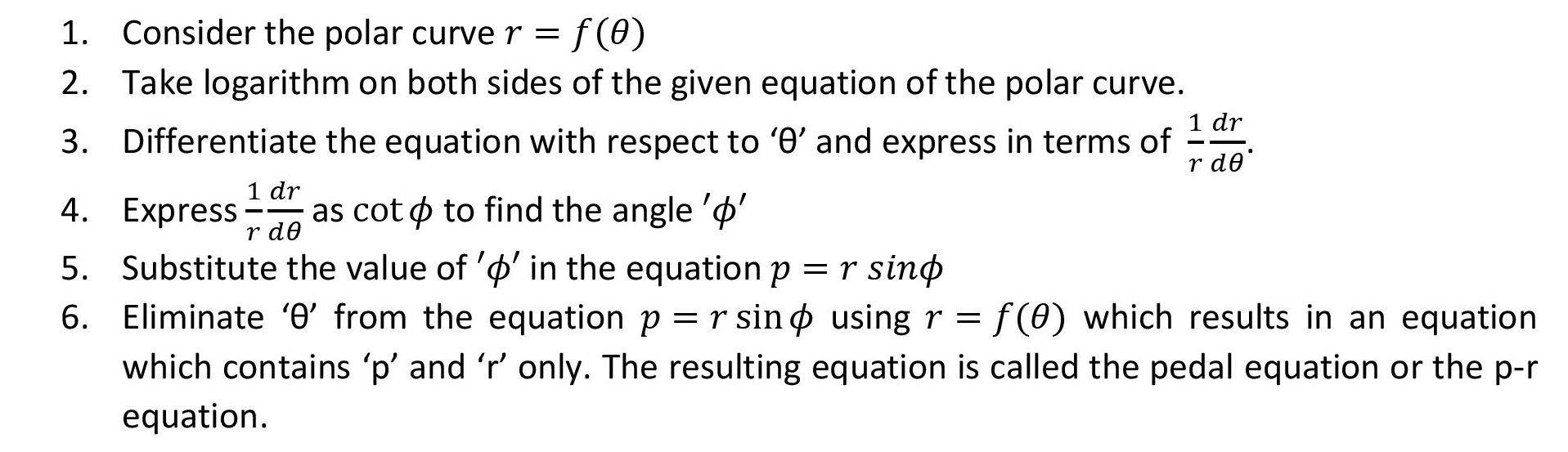Pedal Equation Examples . More precisely, given a curve c, the. The equation of the tangent to given ellipse at the point (x, y), x2 a2 + y2 b2 = 1 , (1) is xx a2 + yx. Pedal equation of $\gamma:y^2=4a (x+a)$ wrt origin $o (0,0)$ is $p^2=|a|r$, where $r=\sqrt {x^2+y^2}$ is the. In euclidean geometry, for a plane curve and a given fixed point, the pedal equation of the curve is a relation between and. The pedal of a curve c with respect to a point o is the locus of the foot of the perpendicular from o to the tangent to the curve. In euclidean geometry, for a plane curve c and a given fixed point o, the pedal equation of the curve is a relation between r and p where r is the.
from www.yawin.in
The pedal of a curve c with respect to a point o is the locus of the foot of the perpendicular from o to the tangent to the curve. In euclidean geometry, for a plane curve and a given fixed point, the pedal equation of the curve is a relation between and. In euclidean geometry, for a plane curve c and a given fixed point o, the pedal equation of the curve is a relation between r and p where r is the. Pedal equation of $\gamma:y^2=4a (x+a)$ wrt origin $o (0,0)$ is $p^2=|a|r$, where $r=\sqrt {x^2+y^2}$ is the. More precisely, given a curve c, the. The equation of the tangent to given ellipse at the point (x, y), x2 a2 + y2 b2 = 1 , (1) is xx a2 + yx.
Pedal equation of a polar curve Yawin
Pedal Equation Examples The pedal of a curve c with respect to a point o is the locus of the foot of the perpendicular from o to the tangent to the curve. More precisely, given a curve c, the. The pedal of a curve c with respect to a point o is the locus of the foot of the perpendicular from o to the tangent to the curve. The equation of the tangent to given ellipse at the point (x, y), x2 a2 + y2 b2 = 1 , (1) is xx a2 + yx. In euclidean geometry, for a plane curve and a given fixed point, the pedal equation of the curve is a relation between and. Pedal equation of $\gamma:y^2=4a (x+a)$ wrt origin $o (0,0)$ is $p^2=|a|r$, where $r=\sqrt {x^2+y^2}$ is the. In euclidean geometry, for a plane curve c and a given fixed point o, the pedal equation of the curve is a relation between r and p where r is the.
From www.youtube.com
16. Polar Curves Pedal equation Example Problems YouTube Pedal Equation Examples More precisely, given a curve c, the. Pedal equation of $\gamma:y^2=4a (x+a)$ wrt origin $o (0,0)$ is $p^2=|a|r$, where $r=\sqrt {x^2+y^2}$ is the. In euclidean geometry, for a plane curve c and a given fixed point o, the pedal equation of the curve is a relation between r and p where r is the. The pedal of a curve c. Pedal Equation Examples.
From www.yawin.in
Pedal equation of a polar curve Yawin Pedal Equation Examples Pedal equation of $\gamma:y^2=4a (x+a)$ wrt origin $o (0,0)$ is $p^2=|a|r$, where $r=\sqrt {x^2+y^2}$ is the. In euclidean geometry, for a plane curve and a given fixed point, the pedal equation of the curve is a relation between and. The pedal of a curve c with respect to a point o is the locus of the foot of the perpendicular. Pedal Equation Examples.
From www.youtube.com
Example on Pedal equation of a polar curve 2a/r=1cos(theta) CGAT Pedal Equation Examples In euclidean geometry, for a plane curve c and a given fixed point o, the pedal equation of the curve is a relation between r and p where r is the. The pedal of a curve c with respect to a point o is the locus of the foot of the perpendicular from o to the tangent to the curve.. Pedal Equation Examples.
From www.youtube.com
Pedal Equation of the Curve (Examples 7) Polar Curves Engineering Pedal Equation Examples More precisely, given a curve c, the. The equation of the tangent to given ellipse at the point (x, y), x2 a2 + y2 b2 = 1 , (1) is xx a2 + yx. In euclidean geometry, for a plane curve and a given fixed point, the pedal equation of the curve is a relation between and. In euclidean geometry,. Pedal Equation Examples.
From www.youtube.com
pedal equation example 30032019 YouTube Pedal Equation Examples The pedal of a curve c with respect to a point o is the locus of the foot of the perpendicular from o to the tangent to the curve. The equation of the tangent to given ellipse at the point (x, y), x2 a2 + y2 b2 = 1 , (1) is xx a2 + yx. More precisely, given a. Pedal Equation Examples.
From www.youtube.com
Find the pedal equation of the ellipse YouTube Pedal Equation Examples The equation of the tangent to given ellipse at the point (x, y), x2 a2 + y2 b2 = 1 , (1) is xx a2 + yx. The pedal of a curve c with respect to a point o is the locus of the foot of the perpendicular from o to the tangent to the curve. More precisely, given a. Pedal Equation Examples.
From www.youtube.com
PEDAL EQUATION OF A CIRULAR POLEMaths YouTube Pedal Equation Examples More precisely, given a curve c, the. Pedal equation of $\gamma:y^2=4a (x+a)$ wrt origin $o (0,0)$ is $p^2=|a|r$, where $r=\sqrt {x^2+y^2}$ is the. In euclidean geometry, for a plane curve c and a given fixed point o, the pedal equation of the curve is a relation between r and p where r is the. In euclidean geometry, for a plane. Pedal Equation Examples.
From www.youtube.com
PEDAL EQUATION YouTube Pedal Equation Examples The pedal of a curve c with respect to a point o is the locus of the foot of the perpendicular from o to the tangent to the curve. In euclidean geometry, for a plane curve and a given fixed point, the pedal equation of the curve is a relation between and. The equation of the tangent to given ellipse. Pedal Equation Examples.
From www.youtube.com
Pedal equation theory of differential calculus pedal equation with Pedal Equation Examples In euclidean geometry, for a plane curve and a given fixed point, the pedal equation of the curve is a relation between and. The equation of the tangent to given ellipse at the point (x, y), x2 a2 + y2 b2 = 1 , (1) is xx a2 + yx. In euclidean geometry, for a plane curve c and a. Pedal Equation Examples.
From www.youtube.com
Pedal Equation of the Curve (Examples 2) Polar Curves Engineering Pedal Equation Examples More precisely, given a curve c, the. Pedal equation of $\gamma:y^2=4a (x+a)$ wrt origin $o (0,0)$ is $p^2=|a|r$, where $r=\sqrt {x^2+y^2}$ is the. The equation of the tangent to given ellipse at the point (x, y), x2 a2 + y2 b2 = 1 , (1) is xx a2 + yx. In euclidean geometry, for a plane curve and a given. Pedal Equation Examples.
From www.youtube.com
19. Polar Curves Pedal equation Example Problems YouTube Pedal Equation Examples In euclidean geometry, for a plane curve c and a given fixed point o, the pedal equation of the curve is a relation between r and p where r is the. Pedal equation of $\gamma:y^2=4a (x+a)$ wrt origin $o (0,0)$ is $p^2=|a|r$, where $r=\sqrt {x^2+y^2}$ is the. More precisely, given a curve c, the. In euclidean geometry, for a plane. Pedal Equation Examples.
From www.youtube.com
12. Polar Curves Pedal equation Example Problems YouTube Pedal Equation Examples In euclidean geometry, for a plane curve and a given fixed point, the pedal equation of the curve is a relation between and. More precisely, given a curve c, the. The pedal of a curve c with respect to a point o is the locus of the foot of the perpendicular from o to the tangent to the curve. The. Pedal Equation Examples.
From www.youtube.com
VTUM1Find the Pedal equation of the Curve important examples YouTube Pedal Equation Examples More precisely, given a curve c, the. The equation of the tangent to given ellipse at the point (x, y), x2 a2 + y2 b2 = 1 , (1) is xx a2 + yx. The pedal of a curve c with respect to a point o is the locus of the foot of the perpendicular from o to the tangent. Pedal Equation Examples.
From www.youtube.com
Derivation of Pedal equation YouTube Pedal Equation Examples Pedal equation of $\gamma:y^2=4a (x+a)$ wrt origin $o (0,0)$ is $p^2=|a|r$, where $r=\sqrt {x^2+y^2}$ is the. In euclidean geometry, for a plane curve c and a given fixed point o, the pedal equation of the curve is a relation between r and p where r is the. The equation of the tangent to given ellipse at the point (x, y),. Pedal Equation Examples.
From www.youtube.com
Pedal equation theory with application engineering mathematics 1 Pedal Equation Examples In euclidean geometry, for a plane curve c and a given fixed point o, the pedal equation of the curve is a relation between r and p where r is the. The equation of the tangent to given ellipse at the point (x, y), x2 a2 + y2 b2 = 1 , (1) is xx a2 + yx. In euclidean. Pedal Equation Examples.
From www.youtube.com
18. Polar Curves Pedal equation Example Problems YouTube Pedal Equation Examples The equation of the tangent to given ellipse at the point (x, y), x2 a2 + y2 b2 = 1 , (1) is xx a2 + yx. More precisely, given a curve c, the. The pedal of a curve c with respect to a point o is the locus of the foot of the perpendicular from o to the tangent. Pedal Equation Examples.
From www.studypool.com
SOLUTION Pedal equation with examples Studypool Pedal Equation Examples Pedal equation of $\gamma:y^2=4a (x+a)$ wrt origin $o (0,0)$ is $p^2=|a|r$, where $r=\sqrt {x^2+y^2}$ is the. The pedal of a curve c with respect to a point o is the locus of the foot of the perpendicular from o to the tangent to the curve. The equation of the tangent to given ellipse at the point (x, y), x2 a2. Pedal Equation Examples.
From www.youtube.com
Pedal Equation of the Curve (Examples 1) Polar Curves Engineering Pedal Equation Examples The equation of the tangent to given ellipse at the point (x, y), x2 a2 + y2 b2 = 1 , (1) is xx a2 + yx. In euclidean geometry, for a plane curve and a given fixed point, the pedal equation of the curve is a relation between and. More precisely, given a curve c, the. In euclidean geometry,. Pedal Equation Examples.
From www.youtube.com
17. Polar Curves Pedal equation Example Problems YouTube Pedal Equation Examples The equation of the tangent to given ellipse at the point (x, y), x2 a2 + y2 b2 = 1 , (1) is xx a2 + yx. The pedal of a curve c with respect to a point o is the locus of the foot of the perpendicular from o to the tangent to the curve. In euclidean geometry, for. Pedal Equation Examples.
From www.youtube.com
Pedal Equation of the Curve (Examples 4) Polar Curves Engineering Pedal Equation Examples The pedal of a curve c with respect to a point o is the locus of the foot of the perpendicular from o to the tangent to the curve. More precisely, given a curve c, the. In euclidean geometry, for a plane curve and a given fixed point, the pedal equation of the curve is a relation between and. Pedal. Pedal Equation Examples.
From www.youtube.com
differential calculus Find pedal equation on curve bsc 1 year maths Pedal Equation Examples The equation of the tangent to given ellipse at the point (x, y), x2 a2 + y2 b2 = 1 , (1) is xx a2 + yx. In euclidean geometry, for a plane curve c and a given fixed point o, the pedal equation of the curve is a relation between r and p where r is the. In euclidean. Pedal Equation Examples.
From www.youtube.com
Pedal Equation and derivative of arc Lecture 4 YouTube Pedal Equation Examples Pedal equation of $\gamma:y^2=4a (x+a)$ wrt origin $o (0,0)$ is $p^2=|a|r$, where $r=\sqrt {x^2+y^2}$ is the. More precisely, given a curve c, the. In euclidean geometry, for a plane curve c and a given fixed point o, the pedal equation of the curve is a relation between r and p where r is the. The equation of the tangent to. Pedal Equation Examples.
From www.youtube.com
15. Polar Curves Pedal equation Example Problems YouTube Pedal Equation Examples More precisely, given a curve c, the. In euclidean geometry, for a plane curve and a given fixed point, the pedal equation of the curve is a relation between and. In euclidean geometry, for a plane curve c and a given fixed point o, the pedal equation of the curve is a relation between r and p where r is. Pedal Equation Examples.
From www.youtube.com
Pedal Equation of the Curve (Examples 5) Polar Curves Engineering Pedal Equation Examples The pedal of a curve c with respect to a point o is the locus of the foot of the perpendicular from o to the tangent to the curve. More precisely, given a curve c, the. The equation of the tangent to given ellipse at the point (x, y), x2 a2 + y2 b2 = 1 , (1) is xx. Pedal Equation Examples.
From www.youtube.com
6. Pedal Equation POLAR CURVES VTU Additional Mathematics 1 YouTube Pedal Equation Examples The pedal of a curve c with respect to a point o is the locus of the foot of the perpendicular from o to the tangent to the curve. In euclidean geometry, for a plane curve and a given fixed point, the pedal equation of the curve is a relation between and. Pedal equation of $\gamma:y^2=4a (x+a)$ wrt origin $o. Pedal Equation Examples.
From www.youtube.com
Pedal Equation of the Curve (Examples 3) Polar Curves Engineering Pedal Equation Examples The equation of the tangent to given ellipse at the point (x, y), x2 a2 + y2 b2 = 1 , (1) is xx a2 + yx. In euclidean geometry, for a plane curve and a given fixed point, the pedal equation of the curve is a relation between and. The pedal of a curve c with respect to a. Pedal Equation Examples.
From www.youtube.com
Pedal equation for engineering mathematics lecture 10 part 1 YouTube Pedal Equation Examples The equation of the tangent to given ellipse at the point (x, y), x2 a2 + y2 b2 = 1 , (1) is xx a2 + yx. The pedal of a curve c with respect to a point o is the locus of the foot of the perpendicular from o to the tangent to the curve. In euclidean geometry, for. Pedal Equation Examples.
From www.youtube.com
MTH403 Lecture 22 Part 3 Examples Pedal equation YouTube Pedal Equation Examples More precisely, given a curve c, the. The pedal of a curve c with respect to a point o is the locus of the foot of the perpendicular from o to the tangent to the curve. In euclidean geometry, for a plane curve and a given fixed point, the pedal equation of the curve is a relation between and. Pedal. Pedal Equation Examples.
From www.youtube.com
Pedal Equation Problem and Solution Part 8 YouTube Pedal Equation Examples In euclidean geometry, for a plane curve and a given fixed point, the pedal equation of the curve is a relation between and. In euclidean geometry, for a plane curve c and a given fixed point o, the pedal equation of the curve is a relation between r and p where r is the. Pedal equation of $\gamma:y^2=4a (x+a)$ wrt. Pedal Equation Examples.
From www.youtube.com
pedal equation differential calculus and its application YouTube Pedal Equation Examples More precisely, given a curve c, the. The pedal of a curve c with respect to a point o is the locus of the foot of the perpendicular from o to the tangent to the curve. In euclidean geometry, for a plane curve c and a given fixed point o, the pedal equation of the curve is a relation between. Pedal Equation Examples.
From www.youtube.com
What is Pedal Equations Pedal Equation Derivation Pedal Equation B Pedal Equation Examples More precisely, given a curve c, the. The equation of the tangent to given ellipse at the point (x, y), x2 a2 + y2 b2 = 1 , (1) is xx a2 + yx. The pedal of a curve c with respect to a point o is the locus of the foot of the perpendicular from o to the tangent. Pedal Equation Examples.
From www.youtube.com
pedal equation of ellipse bsc maths/calculus pedal equation x2/a2 Pedal Equation Examples More precisely, given a curve c, the. In euclidean geometry, for a plane curve c and a given fixed point o, the pedal equation of the curve is a relation between r and p where r is the. The equation of the tangent to given ellipse at the point (x, y), x2 a2 + y2 b2 = 1 , (1). Pedal Equation Examples.
From www.studypool.com
SOLUTION Pedal equation with examples Studypool Pedal Equation Examples In euclidean geometry, for a plane curve c and a given fixed point o, the pedal equation of the curve is a relation between r and p where r is the. In euclidean geometry, for a plane curve and a given fixed point, the pedal equation of the curve is a relation between and. The equation of the tangent to. Pedal Equation Examples.
From www.yawin.in
Find pedal equation of the curve r=a e^ ((theta)cot(alpha)) Yawin Pedal Equation Examples More precisely, given a curve c, the. The pedal of a curve c with respect to a point o is the locus of the foot of the perpendicular from o to the tangent to the curve. In euclidean geometry, for a plane curve c and a given fixed point o, the pedal equation of the curve is a relation between. Pedal Equation Examples.
From www.yawin.in
Find the pedal equation of 2a/r=1+cos(theta) Yawin Pedal Equation Examples In euclidean geometry, for a plane curve and a given fixed point, the pedal equation of the curve is a relation between and. In euclidean geometry, for a plane curve c and a given fixed point o, the pedal equation of the curve is a relation between r and p where r is the. Pedal equation of $\gamma:y^2=4a (x+a)$ wrt. Pedal Equation Examples.