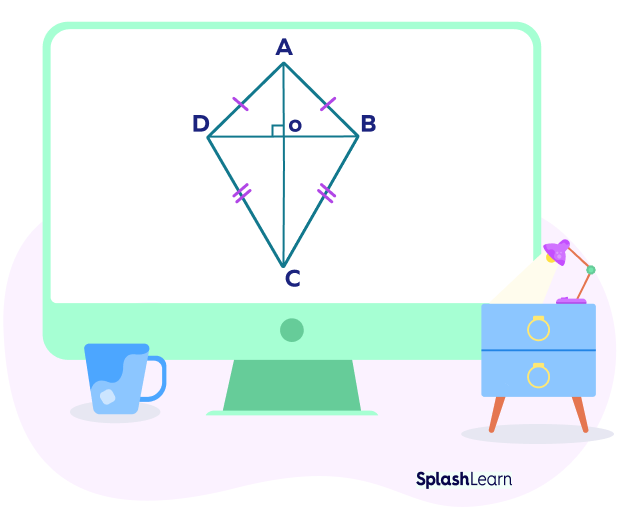
Kite Length Of Diagonals . All its interior angles measure less than 180°. To find diagonal, we have the following ways. One diagonal is twice the length of the other diagonal. The total area of the kite is. (i) from the given area and one diagonal, find the other diagonal. D_2$ are lengths of diagonals. A dart or an arrowhead is a concave kite. The area of kite $= \frac {1} {2} \times d_1 \times d_2$, where $d_1,\; How to find diagonal of a kite. Examples, practice problems on this topic. In most cases, there are two pairs of congruent sides of a kite, that. Find the length of each interior diagonal. The diagonals of a kite intersect at 90 ∘ ∘. A kite has two perpendicular interior diagonals. The formula for the area of a kite is area = 1 2 1 2 (diagonal 1) (diagonal 2) back to quadrilaterals.
from www.splashlearn.com
One diagonal is twice the length of the other diagonal. The diagonals of a kite intersect at 90 ∘ ∘. A dart or an arrowhead is a concave kite. The area of kite $= \frac {1} {2} \times d_1 \times d_2$, where $d_1,\; Examples, practice problems on this topic. The total area of the kite is. The formula for the area of a kite is area = 1 2 1 2 (diagonal 1) (diagonal 2) back to quadrilaterals. In most cases, there are two pairs of congruent sides of a kite, that. Perimeter of a kite with sides a and b is given. To find diagonal, we have the following ways.
Properties of a Kite Definition, Diagonals, Examples, Facts
Kite Length Of Diagonals A kite has two perpendicular interior diagonals. The total area of the kite is. (ii) using pythagorean theorem, find. One diagonal is twice the length of the other diagonal. Find the length of each interior diagonal. The formula for the area of a kite is area = 1 2 1 2 (diagonal 1) (diagonal 2) back to quadrilaterals. In most cases, there are two pairs of congruent sides of a kite, that. A kite has two perpendicular interior diagonals. The diagonals of a kite intersect at 90 ∘ ∘. A dart or an arrowhead is a concave kite. One interior angle is greater than 180°. The area of kite $= \frac {1} {2} \times d_1 \times d_2$, where $d_1,\; D_2$ are lengths of diagonals. Examples, practice problems on this topic. The area of a kite is often calculated based on the length of the diagonals, d 1 and d 2, using the equation: To find diagonal, we have the following ways.
From www.geogebra.org
Kite and Diagonals GeoGebra Kite Length Of Diagonals The diagonals of a kite intersect at 90 ∘ ∘. The formula for the area of a kite is area = 1 2 1 2 (diagonal 1) (diagonal 2) back to quadrilaterals. Examples, practice problems on this topic. In most cases, there are two pairs of congruent sides of a kite, that. All its interior angles measure less than 180°.. Kite Length Of Diagonals.
From ar.inspiredpencil.com
Area Of A Kite Formula Kite Length Of Diagonals Examples, practice problems on this topic. In most cases, there are two pairs of congruent sides of a kite, that. A dart or an arrowhead is a concave kite. Perimeter of a kite with sides a and b is given. To find diagonal, we have the following ways. A kite has two perpendicular interior diagonals. One interior angle is greater. Kite Length Of Diagonals.
From schematicmaxeywheezle.z21.web.core.windows.net
Characteristics Of A Kite Geometry Kite Length Of Diagonals Find the length of each interior diagonal. The total area of the kite is. (ii) using pythagorean theorem, find. The area of kite $= \frac {1} {2} \times d_1 \times d_2$, where $d_1,\; One diagonal is twice the length of the other diagonal. To find diagonal, we have the following ways. All its interior angles measure less than 180°. D_2$. Kite Length Of Diagonals.
From www.geeksforgeeks.org
Program to calculate the area of Kite Kite Length Of Diagonals To find diagonal, we have the following ways. A dart or an arrowhead is a concave kite. The formula for the area of a kite is area = 1 2 1 2 (diagonal 1) (diagonal 2) back to quadrilaterals. (i) from the given area and one diagonal, find the other diagonal. The total area of the kite is. Examples, practice. Kite Length Of Diagonals.
From www.ck12.org
Kites ( Read ) Geometry CK12 Foundation Kite Length Of Diagonals The diagonals of a kite intersect at 90 ∘ ∘. The area of a kite is often calculated based on the length of the diagonals, d 1 and d 2, using the equation: A dart or an arrowhead is a concave kite. In most cases, there are two pairs of congruent sides of a kite, that. (i) from the given. Kite Length Of Diagonals.
From www.bbc.co.uk
Module 2 (M2) geometry & measures area BBC Bitesize Kite Length Of Diagonals Perimeter of a kite with sides a and b is given. The diagonals of a kite intersect at 90 ∘ ∘. Examples, practice problems on this topic. A kite has two perpendicular interior diagonals. The area of kite $= \frac {1} {2} \times d_1 \times d_2$, where $d_1,\; The area of a kite is often calculated based on the length. Kite Length Of Diagonals.
From murphybedmechanismsforsale.blogspot.com
Geometry Kite Examples Kite Length Of Diagonals The formula for the area of a kite is area = 1 2 1 2 (diagonal 1) (diagonal 2) back to quadrilaterals. The diagonals of a kite intersect at 90 ∘ ∘. To find diagonal, we have the following ways. How to find diagonal of a kite. The total area of the kite is. The area of a kite is. Kite Length Of Diagonals.
From www.varsitytutors.com
How to find the length of the diagonal of a kite Advanced Geometry Kite Length Of Diagonals A kite has two perpendicular interior diagonals. Perimeter of a kite with sides a and b is given. A dart or an arrowhead is a concave kite. (ii) using pythagorean theorem, find. The formula for the area of a kite is area = 1 2 1 2 (diagonal 1) (diagonal 2) back to quadrilaterals. The diagonals of a kite intersect. Kite Length Of Diagonals.
From www.gauthmath.com
Solved NOTTO SCALE ABCD is a kite. The diagonals AC and BD intersect Kite Length Of Diagonals A dart or an arrowhead is a concave kite. One diagonal is twice the length of the other diagonal. Find the length of each interior diagonal. Examples, practice problems on this topic. The formula for the area of a kite is area = 1 2 1 2 (diagonal 1) (diagonal 2) back to quadrilaterals. To find diagonal, we have the. Kite Length Of Diagonals.
From www.slideserve.com
PPT Geometry 66 Kites PowerPoint Presentation ID2721679 Kite Length Of Diagonals Find the length of each interior diagonal. A kite has two perpendicular interior diagonals. (ii) using pythagorean theorem, find. All its interior angles measure less than 180°. D_2$ are lengths of diagonals. The formula for the area of a kite is area = 1 2 1 2 (diagonal 1) (diagonal 2) back to quadrilaterals. The total area of the kite. Kite Length Of Diagonals.
From www.nagwa.com
Question Video Finding the Area of a Kite Given the Length of the Kite Length Of Diagonals Find the length of each interior diagonal. All its interior angles measure less than 180°. The total area of the kite is. Perimeter of a kite with sides a and b is given. The area of kite $= \frac {1} {2} \times d_1 \times d_2$, where $d_1,\; One interior angle is greater than 180°. To find diagonal, we have the. Kite Length Of Diagonals.
From www.showme.com
Kites Sides and diagonals Math ShowMe Kite Length Of Diagonals The area of a kite is often calculated based on the length of the diagonals, d 1 and d 2, using the equation: The total area of the kite is. The diagonals of a kite intersect at 90 ∘ ∘. (i) from the given area and one diagonal, find the other diagonal. Find the length of each interior diagonal. A. Kite Length Of Diagonals.
From www.ck12.org
Kite Properties CK12 Foundation Kite Length Of Diagonals The area of a kite is often calculated based on the length of the diagonals, d 1 and d 2, using the equation: All its interior angles measure less than 180°. A dart or an arrowhead is a concave kite. The diagonals of a kite intersect at 90 ∘ ∘. (i) from the given area and one diagonal, find the. Kite Length Of Diagonals.
From quizlet.com
Prove that the diagonals of a kite are perpendicular to each Quizlet Kite Length Of Diagonals One diagonal is twice the length of the other diagonal. The diagonals of a kite intersect at 90 ∘ ∘. (ii) using pythagorean theorem, find. A kite has two perpendicular interior diagonals. All its interior angles measure less than 180°. The area of a kite is often calculated based on the length of the diagonals, d 1 and d 2,. Kite Length Of Diagonals.
From www.pinterest.com
Kites, Basic Introduction, Geometry in 2020 Organic chemistry tutor Kite Length Of Diagonals In most cases, there are two pairs of congruent sides of a kite, that. All its interior angles measure less than 180°. The formula for the area of a kite is area = 1 2 1 2 (diagonal 1) (diagonal 2) back to quadrilaterals. (ii) using pythagorean theorem, find. The diagonals of a kite intersect at 90 ∘ ∘. The. Kite Length Of Diagonals.
From www.splashlearn.com
Properties of a Kite Definition, Diagonals, Examples, Facts Kite Length Of Diagonals One interior angle is greater than 180°. In most cases, there are two pairs of congruent sides of a kite, that. All its interior angles measure less than 180°. Find the length of each interior diagonal. How to find diagonal of a kite. Perimeter of a kite with sides a and b is given. (ii) using pythagorean theorem, find. One. Kite Length Of Diagonals.
From www.shalom-education.com
Properties of Quadrilaterals Edexcel GCSE Maths Revision Kite Length Of Diagonals A kite has two perpendicular interior diagonals. The diagonals of a kite intersect at 90 ∘ ∘. The formula for the area of a kite is area = 1 2 1 2 (diagonal 1) (diagonal 2) back to quadrilaterals. (i) from the given area and one diagonal, find the other diagonal. Examples, practice problems on this topic. All its interior. Kite Length Of Diagonals.
From www.nagwa.com
Question Video Finding the Area of a Kite given Its Dimensions and One Kite Length Of Diagonals The diagonals of a kite intersect at 90 ∘ ∘. (i) from the given area and one diagonal, find the other diagonal. In most cases, there are two pairs of congruent sides of a kite, that. (ii) using pythagorean theorem, find. Perimeter of a kite with sides a and b is given. Find the length of each interior diagonal. A. Kite Length Of Diagonals.
From www.cuemath.com
Properties of a Kite Angles in a Kite, Kite Diagonals Kite Shape Kite Length Of Diagonals (ii) using pythagorean theorem, find. How to find diagonal of a kite. Find the length of each interior diagonal. The formula for the area of a kite is area = 1 2 1 2 (diagonal 1) (diagonal 2) back to quadrilaterals. Perimeter of a kite with sides a and b is given. One diagonal is twice the length of the. Kite Length Of Diagonals.
From www.geogebra.org
LR703XT3 (Diagonals of a kite) GeoGebra Kite Length Of Diagonals A kite has two perpendicular interior diagonals. (ii) using pythagorean theorem, find. The total area of the kite is. Perimeter of a kite with sides a and b is given. One diagonal is twice the length of the other diagonal. All its interior angles measure less than 180°. Find the length of each interior diagonal. The area of a kite. Kite Length Of Diagonals.
From www.youtube.com
Prove Diagonals of a Kite are Perpendicular YouTube Kite Length Of Diagonals One diagonal is twice the length of the other diagonal. Examples, practice problems on this topic. All its interior angles measure less than 180°. The formula for the area of a kite is area = 1 2 1 2 (diagonal 1) (diagonal 2) back to quadrilaterals. One interior angle is greater than 180°. How to find diagonal of a kite.. Kite Length Of Diagonals.
From quizlet.com
Explain how to construct a kite, given its diagonals. Quizlet Kite Length Of Diagonals The area of kite $= \frac {1} {2} \times d_1 \times d_2$, where $d_1,\; (ii) using pythagorean theorem, find. In most cases, there are two pairs of congruent sides of a kite, that. One interior angle is greater than 180°. A dart or an arrowhead is a concave kite. Find the length of each interior diagonal. (i) from the given. Kite Length Of Diagonals.
From www.gauthmath.com
Solved The lengths of two consecutive sides of kite are 5 cm and 10 cm Kite Length Of Diagonals Perimeter of a kite with sides a and b is given. Examples, practice problems on this topic. A kite has two perpendicular interior diagonals. In most cases, there are two pairs of congruent sides of a kite, that. The area of a kite is often calculated based on the length of the diagonals, d 1 and d 2, using the. Kite Length Of Diagonals.
From www.cuemath.com
Area of a Kite Formula, Definition, Examples Kite Length Of Diagonals Examples, practice problems on this topic. One diagonal is twice the length of the other diagonal. The area of kite $= \frac {1} {2} \times d_1 \times d_2$, where $d_1,\; In most cases, there are two pairs of congruent sides of a kite, that. A kite has two perpendicular interior diagonals. To find diagonal, we have the following ways. The. Kite Length Of Diagonals.
From www.varsitytutors.com
How to find the length of the diagonal of a kite ACT Math Kite Length Of Diagonals The total area of the kite is. How to find diagonal of a kite. Examples, practice problems on this topic. A kite has two perpendicular interior diagonals. (i) from the given area and one diagonal, find the other diagonal. A dart or an arrowhead is a concave kite. Find the length of each interior diagonal. (ii) using pythagorean theorem, find.. Kite Length Of Diagonals.
From www.youtube.com
Proof The diagonals of a kite are perpendicular YouTube Kite Length Of Diagonals A kite has two perpendicular interior diagonals. One diagonal is twice the length of the other diagonal. Examples, practice problems on this topic. (ii) using pythagorean theorem, find. The diagonals of a kite intersect at 90 ∘ ∘. The area of a kite is often calculated based on the length of the diagonals, d 1 and d 2, using the. Kite Length Of Diagonals.
From math.stackexchange.com
geometry Relationships between diagonals in a right kite Kite Length Of Diagonals D_2$ are lengths of diagonals. In most cases, there are two pairs of congruent sides of a kite, that. The area of kite $= \frac {1} {2} \times d_1 \times d_2$, where $d_1,\; The total area of the kite is. Find the length of each interior diagonal. A dart or an arrowhead is a concave kite. The formula for the. Kite Length Of Diagonals.
From www.gauthmath.com
Solved The diagram below shows a kite ABCD. The diagonals cut at right Kite Length Of Diagonals Perimeter of a kite with sides a and b is given. The diagonals of a kite intersect at 90 ∘ ∘. One interior angle is greater than 180°. (ii) using pythagorean theorem, find. The total area of the kite is. D_2$ are lengths of diagonals. In most cases, there are two pairs of congruent sides of a kite, that. A. Kite Length Of Diagonals.
From www.splashlearn.com
Properties of a Kite Definition, Diagonals, Examples, Facts Kite Length Of Diagonals Perimeter of a kite with sides a and b is given. (ii) using pythagorean theorem, find. One diagonal is twice the length of the other diagonal. The formula for the area of a kite is area = 1 2 1 2 (diagonal 1) (diagonal 2) back to quadrilaterals. All its interior angles measure less than 180°. Examples, practice problems on. Kite Length Of Diagonals.
From www.ck12.org
Kites ( Read ) Geometry CK12 Foundation Kite Length Of Diagonals One interior angle is greater than 180°. The area of a kite is often calculated based on the length of the diagonals, d 1 and d 2, using the equation: Examples, practice problems on this topic. D_2$ are lengths of diagonals. One diagonal is twice the length of the other diagonal. Find the length of each interior diagonal. A dart. Kite Length Of Diagonals.
From www.youtube.com
How To Work Out The Area Of A Kite By Multiplying The Diagonal Lengths Kite Length Of Diagonals Perimeter of a kite with sides a and b is given. All its interior angles measure less than 180°. D_2$ are lengths of diagonals. The total area of the kite is. Find the length of each interior diagonal. To find diagonal, we have the following ways. The formula for the area of a kite is area = 1 2 1. Kite Length Of Diagonals.
From www.youtube.com
Finding the lengths of diagonals in a kite YouTube Kite Length Of Diagonals Find the length of each interior diagonal. One diagonal is twice the length of the other diagonal. In most cases, there are two pairs of congruent sides of a kite, that. All its interior angles measure less than 180°. D_2$ are lengths of diagonals. How to find diagonal of a kite. One interior angle is greater than 180°. Perimeter of. Kite Length Of Diagonals.
From www.cuemath.com
Properties of kite Definition of Kite with Solved Examples Cuemath Kite Length Of Diagonals In most cases, there are two pairs of congruent sides of a kite, that. The area of a kite is often calculated based on the length of the diagonals, d 1 and d 2, using the equation: To find diagonal, we have the following ways. A dart or an arrowhead is a concave kite. Find the length of each interior. Kite Length Of Diagonals.
From www.cuemath.com
Properties of kite Definition of Kite with Solved Examples Cuemath Kite Length Of Diagonals The area of a kite is often calculated based on the length of the diagonals, d 1 and d 2, using the equation: A dart or an arrowhead is a concave kite. The diagonals of a kite intersect at 90 ∘ ∘. (i) from the given area and one diagonal, find the other diagonal. The formula for the area of. Kite Length Of Diagonals.
From www.varsitytutors.com
How to find the length of the diagonal of a kite ACT Math Kite Length Of Diagonals How to find diagonal of a kite. A dart or an arrowhead is a concave kite. The total area of the kite is. Find the length of each interior diagonal. (ii) using pythagorean theorem, find. A kite has two perpendicular interior diagonals. (i) from the given area and one diagonal, find the other diagonal. One interior angle is greater than. Kite Length Of Diagonals.