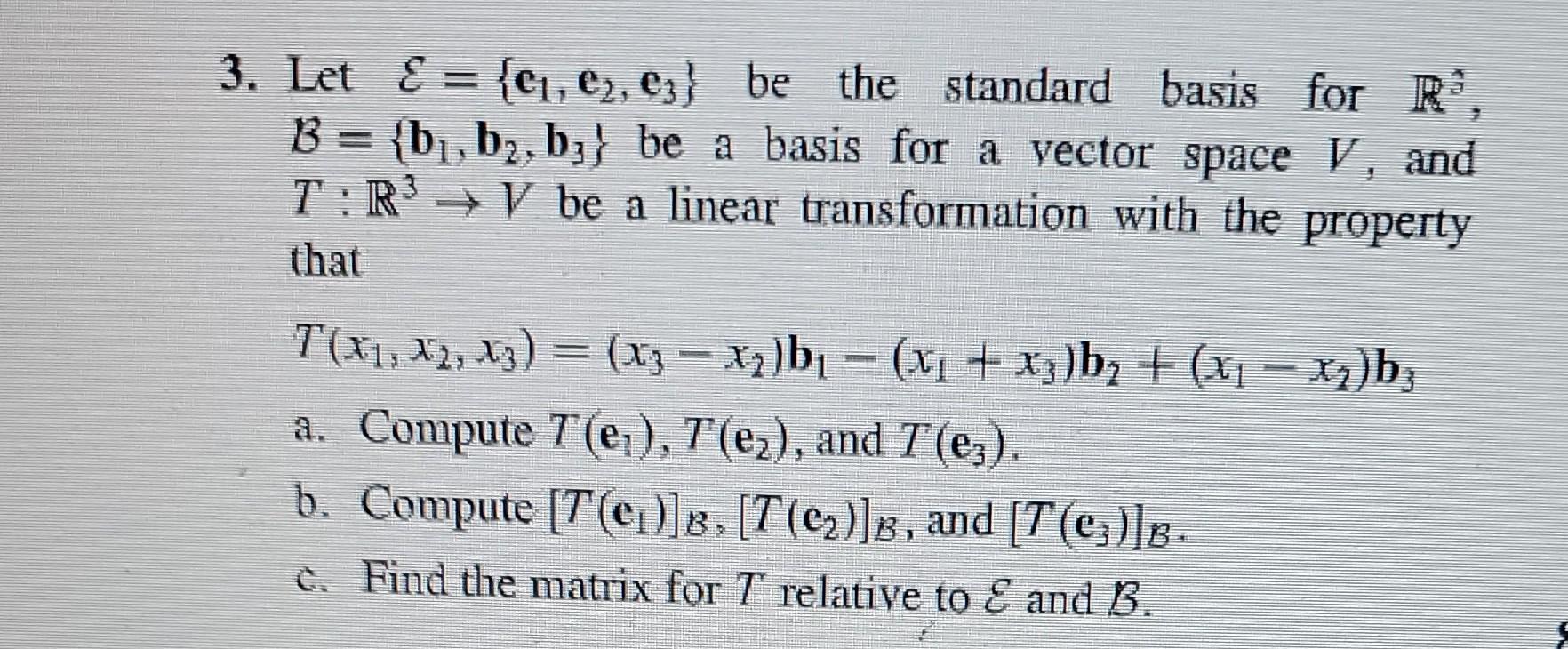Standard Basis For R3 . Every vector (x;y;z) in r3 is a unique linear combination of the standard basis. So if $x = (x,y,z) \in \mathbb{r}^3$, it has the form $$x = (x,y,z) =. Since for any vector x = (x 1, x 2, x 3) in r 3, the standard basis vectors in r 3 are. In particular, \(\mathbb{r}^n \) has dimension \(n\). This is sometimes known as the standard basis. The standard basis is $e_1 = (1,0,0)$, $e_2 = (0,1,0)$, and $e_3 = (0,0,1)$. A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. Note if three vectors are linearly independent in r^3, they. Form a basis for \(\mathbb{r}^n \). Any vector x in r 3 may. Standard basis vectors in r 3.
from www.chegg.com
Every vector (x;y;z) in r3 is a unique linear combination of the standard basis. This is sometimes known as the standard basis. The standard basis is $e_1 = (1,0,0)$, $e_2 = (0,1,0)$, and $e_3 = (0,0,1)$. Any vector x in r 3 may. Form a basis for \(\mathbb{r}^n \). Since for any vector x = (x 1, x 2, x 3) in r 3, the standard basis vectors in r 3 are. In particular, \(\mathbb{r}^n \) has dimension \(n\). A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. So if $x = (x,y,z) \in \mathbb{r}^3$, it has the form $$x = (x,y,z) =. Note if three vectors are linearly independent in r^3, they.
Solved 3. Let E={e1,e2,e3} be the standard basis for R3,
Standard Basis For R3 This is sometimes known as the standard basis. Any vector x in r 3 may. A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. In particular, \(\mathbb{r}^n \) has dimension \(n\). Note if three vectors are linearly independent in r^3, they. Since for any vector x = (x 1, x 2, x 3) in r 3, the standard basis vectors in r 3 are. Standard basis vectors in r 3. So if $x = (x,y,z) \in \mathbb{r}^3$, it has the form $$x = (x,y,z) =. This is sometimes known as the standard basis. Form a basis for \(\mathbb{r}^n \). Every vector (x;y;z) in r3 is a unique linear combination of the standard basis. The standard basis is $e_1 = (1,0,0)$, $e_2 = (0,1,0)$, and $e_3 = (0,0,1)$.
From www.chegg.com
Solved Consider the standard basis for R3,B={e1,e2,e3} and Standard Basis For R3 This is sometimes known as the standard basis. In particular, \(\mathbb{r}^n \) has dimension \(n\). Form a basis for \(\mathbb{r}^n \). Since for any vector x = (x 1, x 2, x 3) in r 3, the standard basis vectors in r 3 are. Standard basis vectors in r 3. So if $x = (x,y,z) \in \mathbb{r}^3$, it has the. Standard Basis For R3.
From www.chegg.com
Solved Let E={e1,e2,e;} be the standard basis for R3 and B = Standard Basis For R3 So if $x = (x,y,z) \in \mathbb{r}^3$, it has the form $$x = (x,y,z) =. Any vector x in r 3 may. Since for any vector x = (x 1, x 2, x 3) in r 3, the standard basis vectors in r 3 are. Standard basis vectors in r 3. In particular, \(\mathbb{r}^n \) has dimension \(n\). Note if. Standard Basis For R3.
From www.youtube.com
Linear Algebra Check if a set is a basis of R^3 YouTube Standard Basis For R3 This is sometimes known as the standard basis. Since for any vector x = (x 1, x 2, x 3) in r 3, the standard basis vectors in r 3 are. Note if three vectors are linearly independent in r^3, they. Any vector x in r 3 may. The standard basis is $e_1 = (1,0,0)$, $e_2 = (0,1,0)$, and $e_3. Standard Basis For R3.
From www.youtube.com
Basis Examples for Vector Spaces R^3 and Pn (Linear Independence and Standard Basis For R3 This is sometimes known as the standard basis. In particular, \(\mathbb{r}^n \) has dimension \(n\). Since for any vector x = (x 1, x 2, x 3) in r 3, the standard basis vectors in r 3 are. Note if three vectors are linearly independent in r^3, they. Standard basis vectors in r 3. So if $x = (x,y,z) \in. Standard Basis For R3.
From www.chegg.com
Solved Suppose A is the matrix for TR3→R3 relative to the Standard Basis For R3 The standard basis is $e_1 = (1,0,0)$, $e_2 = (0,1,0)$, and $e_3 = (0,0,1)$. This is sometimes known as the standard basis. Standard basis vectors in r 3. So if $x = (x,y,z) \in \mathbb{r}^3$, it has the form $$x = (x,y,z) =. Form a basis for \(\mathbb{r}^n \). Note if three vectors are linearly independent in r^3, they. Any. Standard Basis For R3.
From www.youtube.com
Finding a Standard Matrix Using the Standard Basis YouTube Standard Basis For R3 Note if three vectors are linearly independent in r^3, they. The standard basis is $e_1 = (1,0,0)$, $e_2 = (0,1,0)$, and $e_3 = (0,0,1)$. Since for any vector x = (x 1, x 2, x 3) in r 3, the standard basis vectors in r 3 are. A standard basis, also called a natural basis, is a special orthonormal vector. Standard Basis For R3.
From www.chegg.com
Solved Suppose A is the matrix for T R3 → R3 relative to Standard Basis For R3 In particular, \(\mathbb{r}^n \) has dimension \(n\). The standard basis is $e_1 = (1,0,0)$, $e_2 = (0,1,0)$, and $e_3 = (0,0,1)$. Note if three vectors are linearly independent in r^3, they. This is sometimes known as the standard basis. Any vector x in r 3 may. Since for any vector x = (x 1, x 2, x 3) in r. Standard Basis For R3.
From www.chegg.com
Solved If e1,e2, and e3 are the standard basis vectors for Standard Basis For R3 Standard basis vectors in r 3. Form a basis for \(\mathbb{r}^n \). A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. In particular, \(\mathbb{r}^n \) has dimension \(n\). Note if three vectors are linearly independent in r^3, they. The standard basis is $e_1 = (1,0,0)$, $e_2 =. Standard Basis For R3.
From www.chegg.com
Solved 10. Let be the standard basis of R3. Consider the Standard Basis For R3 This is sometimes known as the standard basis. So if $x = (x,y,z) \in \mathbb{r}^3$, it has the form $$x = (x,y,z) =. Note if three vectors are linearly independent in r^3, they. A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. Since for any vector x. Standard Basis For R3.
From www.slideserve.com
PPT 5.4 Basis And Dimension PowerPoint Presentation, free download Standard Basis For R3 The standard basis is $e_1 = (1,0,0)$, $e_2 = (0,1,0)$, and $e_3 = (0,0,1)$. Since for any vector x = (x 1, x 2, x 3) in r 3, the standard basis vectors in r 3 are. In particular, \(\mathbb{r}^n \) has dimension \(n\). Every vector (x;y;z) in r3 is a unique linear combination of the standard basis. Note if. Standard Basis For R3.
From www.chegg.com
Solved 1. Let 0 01 be the ordered standard basis in R3, and Standard Basis For R3 Any vector x in r 3 may. Note if three vectors are linearly independent in r^3, they. Standard basis vectors in r 3. Since for any vector x = (x 1, x 2, x 3) in r 3, the standard basis vectors in r 3 are. The standard basis is $e_1 = (1,0,0)$, $e_2 = (0,1,0)$, and $e_3 = (0,0,1)$.. Standard Basis For R3.
From www.numerade.com
Find a standard basis vector for R^{3} that can b… Standard Basis For R3 A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. Standard basis vectors in r 3. Every vector (x;y;z) in r3 is a unique linear combination of the standard basis. Form a basis for \(\mathbb{r}^n \). So if $x = (x,y,z) \in \mathbb{r}^3$, it has the form $$x. Standard Basis For R3.
From www.chegg.com
Solved Suppose A is the matrix for T R3 R3 relative to the Standard Basis For R3 Standard basis vectors in r 3. In particular, \(\mathbb{r}^n \) has dimension \(n\). Form a basis for \(\mathbb{r}^n \). Since for any vector x = (x 1, x 2, x 3) in r 3, the standard basis vectors in r 3 are. Any vector x in r 3 may. The standard basis is $e_1 = (1,0,0)$, $e_2 = (0,1,0)$, and. Standard Basis For R3.
From solvedlib.com
Let e1,e2, e3 be the standard basis vectors in R3 and… SolvedLib Standard Basis For R3 A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. Form a basis for \(\mathbb{r}^n \). Since for any vector x = (x 1, x 2, x 3) in r 3, the standard basis vectors in r 3 are. Any vector x in r 3 may. Note if. Standard Basis For R3.
From www.chegg.com
Solved Let epsilon be the standard basis for R^3, and let B Standard Basis For R3 So if $x = (x,y,z) \in \mathbb{r}^3$, it has the form $$x = (x,y,z) =. Any vector x in r 3 may. In particular, \(\mathbb{r}^n \) has dimension \(n\). The standard basis is $e_1 = (1,0,0)$, $e_2 = (0,1,0)$, and $e_3 = (0,0,1)$. Since for any vector x = (x 1, x 2, x 3) in r 3, the standard. Standard Basis For R3.
From www.chegg.com
Solved 3. Let E={e1,e2,e3} be the standard basis for R3, Standard Basis For R3 Any vector x in r 3 may. A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. Standard basis vectors in r 3. Form a basis for \(\mathbb{r}^n \). Since for any vector x = (x 1, x 2, x 3) in r 3, the standard basis vectors. Standard Basis For R3.
From www.chegg.com
Solved Let. S = (e1, e2, e3) 1m; the standard basis of R3. Standard Basis For R3 In particular, \(\mathbb{r}^n \) has dimension \(n\). So if $x = (x,y,z) \in \mathbb{r}^3$, it has the form $$x = (x,y,z) =. The standard basis is $e_1 = (1,0,0)$, $e_2 = (0,1,0)$, and $e_3 = (0,0,1)$. Note if three vectors are linearly independent in r^3, they. Any vector x in r 3 may. Every vector (x;y;z) in r3 is a. Standard Basis For R3.
From www.chegg.com
Solved Suppose A is the matrix for T R3 R3 relative to the Standard Basis For R3 Since for any vector x = (x 1, x 2, x 3) in r 3, the standard basis vectors in r 3 are. The standard basis is $e_1 = (1,0,0)$, $e_2 = (0,1,0)$, and $e_3 = (0,0,1)$. So if $x = (x,y,z) \in \mathbb{r}^3$, it has the form $$x = (x,y,z) =. Standard basis vectors in r 3. Note if. Standard Basis For R3.
From calcworkshop.com
Basis of Vector Spaces (A Linear Algebra Guide) Standard Basis For R3 Note if three vectors are linearly independent in r^3, they. Standard basis vectors in r 3. This is sometimes known as the standard basis. The standard basis is $e_1 = (1,0,0)$, $e_2 = (0,1,0)$, and $e_3 = (0,0,1)$. Any vector x in r 3 may. Since for any vector x = (x 1, x 2, x 3) in r 3,. Standard Basis For R3.
From www.chegg.com
Solved S = (0 is a basis for R3. Consider the vector XS 2 Standard Basis For R3 Note if three vectors are linearly independent in r^3, they. In particular, \(\mathbb{r}^n \) has dimension \(n\). A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. The standard basis is $e_1 = (1,0,0)$, $e_2 = (0,1,0)$, and $e_3 = (0,0,1)$. Standard basis vectors in r 3. So. Standard Basis For R3.
From www.chegg.com
Solved 10. Let 1M 0 be the standard basis of R3. Consider Standard Basis For R3 Standard basis vectors in r 3. Note if three vectors are linearly independent in r^3, they. Every vector (x;y;z) in r3 is a unique linear combination of the standard basis. The standard basis is $e_1 = (1,0,0)$, $e_2 = (0,1,0)$, and $e_3 = (0,0,1)$. Any vector x in r 3 may. A standard basis, also called a natural basis, is. Standard Basis For R3.
From www.numerade.com
SOLVED Let E be the standard basis of R3 and another basis given by B Standard Basis For R3 Standard basis vectors in r 3. Every vector (x;y;z) in r3 is a unique linear combination of the standard basis. Form a basis for \(\mathbb{r}^n \). This is sometimes known as the standard basis. So if $x = (x,y,z) \in \mathbb{r}^3$, it has the form $$x = (x,y,z) =. Any vector x in r 3 may. Note if three vectors. Standard Basis For R3.
From fyogtzxon.blob.core.windows.net
Standard Basis Vectors For R3 at Nicholas Rodgers blog Standard Basis For R3 Form a basis for \(\mathbb{r}^n \). Standard basis vectors in r 3. Every vector (x;y;z) in r3 is a unique linear combination of the standard basis. Any vector x in r 3 may. This is sometimes known as the standard basis. Note if three vectors are linearly independent in r^3, they. The standard basis is $e_1 = (1,0,0)$, $e_2 =. Standard Basis For R3.
From www.chegg.com
Solved Suppose A is the matrix for TR3→R3 relative to the Standard Basis For R3 Since for any vector x = (x 1, x 2, x 3) in r 3, the standard basis vectors in r 3 are. In particular, \(\mathbb{r}^n \) has dimension \(n\). So if $x = (x,y,z) \in \mathbb{r}^3$, it has the form $$x = (x,y,z) =. Every vector (x;y;z) in r3 is a unique linear combination of the standard basis. Any. Standard Basis For R3.
From www.chegg.com
Solved 5. Let E={e1,e2,e3} be the standard basis for R3 and Standard Basis For R3 Standard basis vectors in r 3. Every vector (x;y;z) in r3 is a unique linear combination of the standard basis. In particular, \(\mathbb{r}^n \) has dimension \(n\). So if $x = (x,y,z) \in \mathbb{r}^3$, it has the form $$x = (x,y,z) =. A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis. Standard Basis For R3.
From www.chegg.com
Solved Suppose A is the matrix for TR3→R3 relative to the Standard Basis For R3 Note if three vectors are linearly independent in r^3, they. Standard basis vectors in r 3. Any vector x in r 3 may. This is sometimes known as the standard basis. Form a basis for \(\mathbb{r}^n \). Since for any vector x = (x 1, x 2, x 3) in r 3, the standard basis vectors in r 3 are.. Standard Basis For R3.
From www.slideserve.com
PPT Quantum Computing PowerPoint Presentation, free download ID6832149 Standard Basis For R3 A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. Since for any vector x = (x 1, x 2, x 3) in r 3, the standard basis vectors in r 3 are. This is sometimes known as the standard basis. The standard basis is $e_1 = (1,0,0)$,. Standard Basis For R3.
From www.chegg.com
Solved Let B be the following ordered bases of R3 ( [0] Standard Basis For R3 A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. This is sometimes known as the standard basis. Note if three vectors are linearly independent in r^3, they. Every vector (x;y;z) in r3 is a unique linear combination of the standard basis. The standard basis is $e_1 =. Standard Basis For R3.
From www.chegg.com
Solved Let B be the following ordered bases of R3 023 and Standard Basis For R3 Note if three vectors are linearly independent in r^3, they. Any vector x in r 3 may. This is sometimes known as the standard basis. Every vector (x;y;z) in r3 is a unique linear combination of the standard basis. The standard basis is $e_1 = (1,0,0)$, $e_2 = (0,1,0)$, and $e_3 = (0,0,1)$. Since for any vector x = (x. Standard Basis For R3.
From www.chegg.com
Solved Consider R3 with the standard inner product given by Standard Basis For R3 Every vector (x;y;z) in r3 is a unique linear combination of the standard basis. Form a basis for \(\mathbb{r}^n \). Any vector x in r 3 may. The standard basis is $e_1 = (1,0,0)$, $e_2 = (0,1,0)$, and $e_3 = (0,0,1)$. So if $x = (x,y,z) \in \mathbb{r}^3$, it has the form $$x = (x,y,z) =. Standard basis vectors in. Standard Basis For R3.
From www.chegg.com
Solved Let E be the standard basis for R3.The set of Standard Basis For R3 Since for any vector x = (x 1, x 2, x 3) in r 3, the standard basis vectors in r 3 are. The standard basis is $e_1 = (1,0,0)$, $e_2 = (0,1,0)$, and $e_3 = (0,0,1)$. So if $x = (x,y,z) \in \mathbb{r}^3$, it has the form $$x = (x,y,z) =. A standard basis, also called a natural basis,. Standard Basis For R3.
From www.chegg.com
Solved Consider the following basis B of R3. Notation E is Standard Basis For R3 Standard basis vectors in r 3. Any vector x in r 3 may. Every vector (x;y;z) in r3 is a unique linear combination of the standard basis. In particular, \(\mathbb{r}^n \) has dimension \(n\). This is sometimes known as the standard basis. A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis. Standard Basis For R3.
From www.chegg.com
Solved Consider the 3 Dimensional vector space R3 with the Standard Basis For R3 Every vector (x;y;z) in r3 is a unique linear combination of the standard basis. Any vector x in r 3 may. Standard basis vectors in r 3. So if $x = (x,y,z) \in \mathbb{r}^3$, it has the form $$x = (x,y,z) =. Since for any vector x = (x 1, x 2, x 3) in r 3, the standard basis. Standard Basis For R3.
From www.chegg.com
Solved Given the transformation T R3 > R3 defined by the Standard Basis For R3 Standard basis vectors in r 3. Any vector x in r 3 may. Form a basis for \(\mathbb{r}^n \). The standard basis is $e_1 = (1,0,0)$, $e_2 = (0,1,0)$, and $e_3 = (0,0,1)$. This is sometimes known as the standard basis. Since for any vector x = (x 1, x 2, x 3) in r 3, the standard basis vectors. Standard Basis For R3.
From www.numerade.com
SOLVED (4 points) Find standard basis vector for R3 that can be added Standard Basis For R3 So if $x = (x,y,z) \in \mathbb{r}^3$, it has the form $$x = (x,y,z) =. Form a basis for \(\mathbb{r}^n \). Any vector x in r 3 may. Every vector (x;y;z) in r3 is a unique linear combination of the standard basis. This is sometimes known as the standard basis. Standard basis vectors in r 3. Since for any vector. Standard Basis For R3.