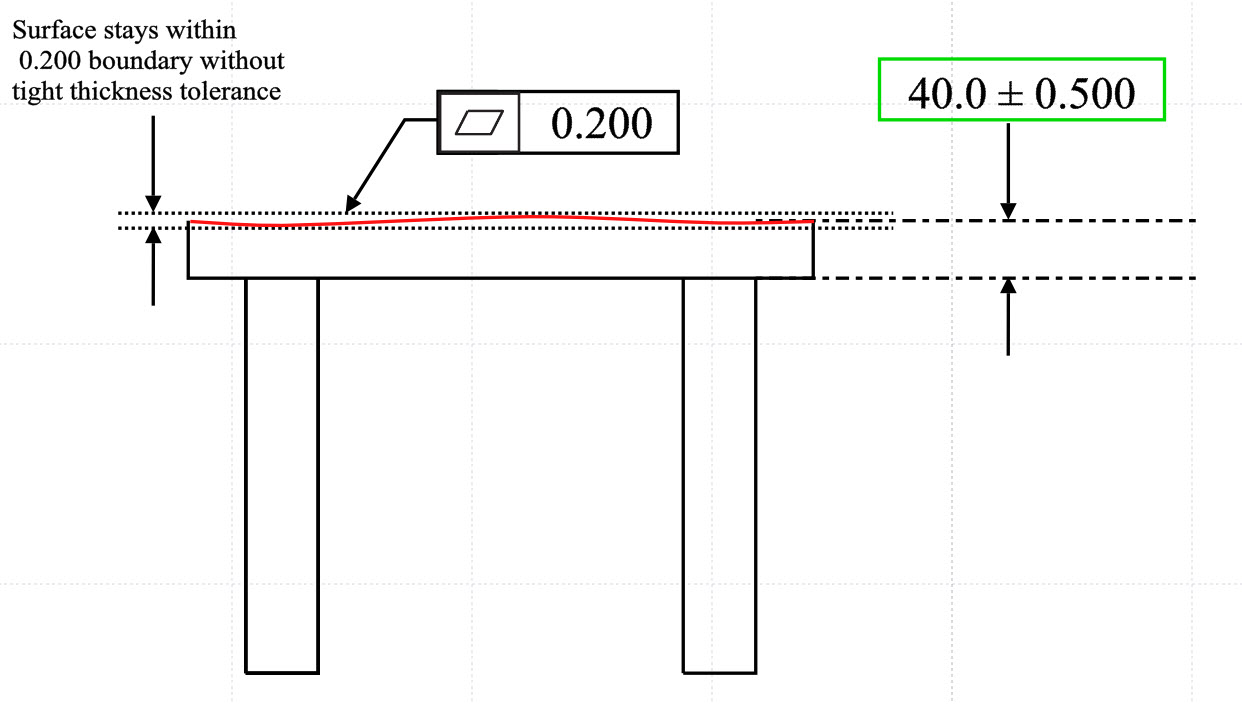
Criteria For Flatness . Let $(r, p)$ be a local ring. By lemma 10.99.8 we see that. A very important class of results, namely criteria for flatness, are discussed in algebra, sections 10.99, 10.101, 10.128, and more on morphisms,. In this section we discuss criteria for flatness. If $\text{tor}_1^ r(m, r/i) = 0$ and $m/im$ is flat over $r/i$, then $m$ is flat over $r$. Flatness is really an algebraic notion with a subtle geometric interpretation. If $m$ is a finitely presented module, then $m$ is flat iff $\mathrm{tor}_{1}^r(m,r/p)=0$. Flatness criteria help determine when a module is flat, including the tensor product and local flatness criteria. It is best explained in terms of modules and illustrated by. The main result in this section is lazard's theorem (theorem 10.81.4 below), which says.
from animalia-life.club
If $\text{tor}_1^ r(m, r/i) = 0$ and $m/im$ is flat over $r/i$, then $m$ is flat over $r$. Let $(r, p)$ be a local ring. Flatness criteria help determine when a module is flat, including the tensor product and local flatness criteria. A very important class of results, namely criteria for flatness, are discussed in algebra, sections 10.99, 10.101, 10.128, and more on morphisms,. It is best explained in terms of modules and illustrated by. In this section we discuss criteria for flatness. By lemma 10.99.8 we see that. If $m$ is a finitely presented module, then $m$ is flat iff $\mathrm{tor}_{1}^r(m,r/p)=0$. Flatness is really an algebraic notion with a subtle geometric interpretation. The main result in this section is lazard's theorem (theorem 10.81.4 below), which says.
Surface Flatness Measurement
Criteria For Flatness In this section we discuss criteria for flatness. Let $(r, p)$ be a local ring. By lemma 10.99.8 we see that. Flatness criteria help determine when a module is flat, including the tensor product and local flatness criteria. A very important class of results, namely criteria for flatness, are discussed in algebra, sections 10.99, 10.101, 10.128, and more on morphisms,. Flatness is really an algebraic notion with a subtle geometric interpretation. It is best explained in terms of modules and illustrated by. In this section we discuss criteria for flatness. If $\text{tor}_1^ r(m, r/i) = 0$ and $m/im$ is flat over $r/i$, then $m$ is flat over $r$. The main result in this section is lazard's theorem (theorem 10.81.4 below), which says. If $m$ is a finitely presented module, then $m$ is flat iff $\mathrm{tor}_{1}^r(m,r/p)=0$.
From www.slideserve.com
PPT Floor Flatness and Levelness PowerPoint Presentation, free Criteria For Flatness Flatness criteria help determine when a module is flat, including the tensor product and local flatness criteria. By lemma 10.99.8 we see that. In this section we discuss criteria for flatness. It is best explained in terms of modules and illustrated by. Flatness is really an algebraic notion with a subtle geometric interpretation. A very important class of results, namely. Criteria For Flatness.
From americanbobcat.blog
MECHANICAL DESIGN ENGINEERING Geometrical Dimensioning and Criteria For Flatness If $\text{tor}_1^ r(m, r/i) = 0$ and $m/im$ is flat over $r/i$, then $m$ is flat over $r$. It is best explained in terms of modules and illustrated by. Flatness criteria help determine when a module is flat, including the tensor product and local flatness criteria. In this section we discuss criteria for flatness. Let $(r, p)$ be a local. Criteria For Flatness.
From slideplayer.com
Design Guidelines for Zn Casting ppt download Criteria For Flatness In this section we discuss criteria for flatness. If $m$ is a finitely presented module, then $m$ is flat iff $\mathrm{tor}_{1}^r(m,r/p)=0$. A very important class of results, namely criteria for flatness, are discussed in algebra, sections 10.99, 10.101, 10.128, and more on morphisms,. If $\text{tor}_1^ r(m, r/i) = 0$ and $m/im$ is flat over $r/i$, then $m$ is flat over. Criteria For Flatness.
From www.researchgate.net
Tabulation of Degree of Flatness with concentration and time Download Criteria For Flatness By lemma 10.99.8 we see that. It is best explained in terms of modules and illustrated by. Flatness is really an algebraic notion with a subtle geometric interpretation. If $\text{tor}_1^ r(m, r/i) = 0$ and $m/im$ is flat over $r/i$, then $m$ is flat over $r$. Flatness criteria help determine when a module is flat, including the tensor product and. Criteria For Flatness.
From www.researchgate.net
Evolution of flatness defect measured according to the three criteria Criteria For Flatness Let $(r, p)$ be a local ring. In this section we discuss criteria for flatness. It is best explained in terms of modules and illustrated by. A very important class of results, namely criteria for flatness, are discussed in algebra, sections 10.99, 10.101, 10.128, and more on morphisms,. Flatness is really an algebraic notion with a subtle geometric interpretation. If. Criteria For Flatness.
From quelltech.de
Measure flatness Efficient & precise monitoring in real time! Criteria For Flatness Flatness is really an algebraic notion with a subtle geometric interpretation. If $m$ is a finitely presented module, then $m$ is flat iff $\mathrm{tor}_{1}^r(m,r/p)=0$. It is best explained in terms of modules and illustrated by. A very important class of results, namely criteria for flatness, are discussed in algebra, sections 10.99, 10.101, 10.128, and more on morphisms,. In this section. Criteria For Flatness.
From mirucoptical.com
Flatness measuring jig MIRUC OPTICAL CO., LTD. Criteria For Flatness The main result in this section is lazard's theorem (theorem 10.81.4 below), which says. Flatness is really an algebraic notion with a subtle geometric interpretation. Let $(r, p)$ be a local ring. A very important class of results, namely criteria for flatness, are discussed in algebra, sections 10.99, 10.101, 10.128, and more on morphisms,. Flatness criteria help determine when a. Criteria For Flatness.
From www.scribd.com
TolerancesOptions Flatness Sheet Metal Engineering Tolerance Criteria For Flatness If $\text{tor}_1^ r(m, r/i) = 0$ and $m/im$ is flat over $r/i$, then $m$ is flat over $r$. It is best explained in terms of modules and illustrated by. Flatness criteria help determine when a module is flat, including the tensor product and local flatness criteria. Flatness is really an algebraic notion with a subtle geometric interpretation. In this section. Criteria For Flatness.
From www.gdandtbasics.com
flatness measurement GD&T Basics Criteria For Flatness If $\text{tor}_1^ r(m, r/i) = 0$ and $m/im$ is flat over $r/i$, then $m$ is flat over $r$. If $m$ is a finitely presented module, then $m$ is flat iff $\mathrm{tor}_{1}^r(m,r/p)=0$. The main result in this section is lazard's theorem (theorem 10.81.4 below), which says. Flatness is really an algebraic notion with a subtle geometric interpretation. It is best explained. Criteria For Flatness.
From animalia-life.club
Surface Flatness Measurement Criteria For Flatness By lemma 10.99.8 we see that. The main result in this section is lazard's theorem (theorem 10.81.4 below), which says. Let $(r, p)$ be a local ring. It is best explained in terms of modules and illustrated by. Flatness criteria help determine when a module is flat, including the tensor product and local flatness criteria. If $m$ is a finitely. Criteria For Flatness.
From www.youtube.com
Surface Finish and Flatness YouTube Criteria For Flatness Flatness is really an algebraic notion with a subtle geometric interpretation. The main result in this section is lazard's theorem (theorem 10.81.4 below), which says. A very important class of results, namely criteria for flatness, are discussed in algebra, sections 10.99, 10.101, 10.128, and more on morphisms,. It is best explained in terms of modules and illustrated by. If $m$. Criteria For Flatness.
From www.riansclub.com
What Is Flatness Tolerance In GD & T Criteria For Flatness If $\text{tor}_1^ r(m, r/i) = 0$ and $m/im$ is flat over $r/i$, then $m$ is flat over $r$. Let $(r, p)$ be a local ring. It is best explained in terms of modules and illustrated by. In this section we discuss criteria for flatness. The main result in this section is lazard's theorem (theorem 10.81.4 below), which says. By lemma. Criteria For Flatness.
From bbs.homeshopmachinist.net
Flatness criteria for surface plates. The Home Shop Machinist Criteria For Flatness In this section we discuss criteria for flatness. Let $(r, p)$ be a local ring. If $\text{tor}_1^ r(m, r/i) = 0$ and $m/im$ is flat over $r/i$, then $m$ is flat over $r$. It is best explained in terms of modules and illustrated by. Flatness is really an algebraic notion with a subtle geometric interpretation. By lemma 10.99.8 we see. Criteria For Flatness.
From vibadirect.com
Flatness Tolerance ViBaDirect Criteria For Flatness Flatness is really an algebraic notion with a subtle geometric interpretation. If $\text{tor}_1^ r(m, r/i) = 0$ and $m/im$ is flat over $r/i$, then $m$ is flat over $r$. It is best explained in terms of modules and illustrated by. Let $(r, p)$ be a local ring. By lemma 10.99.8 we see that. A very important class of results, namely. Criteria For Flatness.
From coretecfloors.art
Ff35 Floor Flatness The Floors Criteria For Flatness By lemma 10.99.8 we see that. A very important class of results, namely criteria for flatness, are discussed in algebra, sections 10.99, 10.101, 10.128, and more on morphisms,. The main result in this section is lazard's theorem (theorem 10.81.4 below), which says. It is best explained in terms of modules and illustrated by. If $\text{tor}_1^ r(m, r/i) = 0$ and. Criteria For Flatness.
From americanbobcat.blog
MECHANICAL DESIGN ENGINEERING Geometrical Dimensioning and Criteria For Flatness In this section we discuss criteria for flatness. The main result in this section is lazard's theorem (theorem 10.81.4 below), which says. Flatness is really an algebraic notion with a subtle geometric interpretation. By lemma 10.99.8 we see that. A very important class of results, namely criteria for flatness, are discussed in algebra, sections 10.99, 10.101, 10.128, and more on. Criteria For Flatness.
From docslib.org
CRITERIA for FLATNESS and INJECTIVITY 3 Ring of R DocsLib Criteria For Flatness If $\text{tor}_1^ r(m, r/i) = 0$ and $m/im$ is flat over $r/i$, then $m$ is flat over $r$. Flatness is really an algebraic notion with a subtle geometric interpretation. It is best explained in terms of modules and illustrated by. The main result in this section is lazard's theorem (theorem 10.81.4 below), which says. Let $(r, p)$ be a local. Criteria For Flatness.
From www.youtube.com
GD&T Basics Flatness YouTube Criteria For Flatness By lemma 10.99.8 we see that. If $\text{tor}_1^ r(m, r/i) = 0$ and $m/im$ is flat over $r/i$, then $m$ is flat over $r$. Let $(r, p)$ be a local ring. Flatness is really an algebraic notion with a subtle geometric interpretation. In this section we discuss criteria for flatness. The main result in this section is lazard's theorem (theorem. Criteria For Flatness.
From www.constructioncanada.net
Concrete chronicles Achieving floor flatness and levelness Criteria For Flatness By lemma 10.99.8 we see that. Let $(r, p)$ be a local ring. Flatness criteria help determine when a module is flat, including the tensor product and local flatness criteria. In this section we discuss criteria for flatness. If $\text{tor}_1^ r(m, r/i) = 0$ and $m/im$ is flat over $r/i$, then $m$ is flat over $r$. If $m$ is a. Criteria For Flatness.
From mavink.com
Flatness Tolerance Chart Criteria For Flatness By lemma 10.99.8 we see that. In this section we discuss criteria for flatness. The main result in this section is lazard's theorem (theorem 10.81.4 below), which says. Let $(r, p)$ be a local ring. Flatness is really an algebraic notion with a subtle geometric interpretation. If $m$ is a finitely presented module, then $m$ is flat iff $\mathrm{tor}_{1}^r(m,r/p)=0$. Flatness. Criteria For Flatness.
From www.chegg.com
Solved Question 11 (1 point) The tolerance zone for flatness Criteria For Flatness The main result in this section is lazard's theorem (theorem 10.81.4 below), which says. Flatness is really an algebraic notion with a subtle geometric interpretation. Let $(r, p)$ be a local ring. If $\text{tor}_1^ r(m, r/i) = 0$ and $m/im$ is flat over $r/i$, then $m$ is flat over $r$. It is best explained in terms of modules and illustrated. Criteria For Flatness.
From www.faro.com
How to evaluate flatness in GD&T Article FARO Criteria For Flatness Let $(r, p)$ be a local ring. By lemma 10.99.8 we see that. If $m$ is a finitely presented module, then $m$ is flat iff $\mathrm{tor}_{1}^r(m,r/p)=0$. A very important class of results, namely criteria for flatness, are discussed in algebra, sections 10.99, 10.101, 10.128, and more on morphisms,. If $\text{tor}_1^ r(m, r/i) = 0$ and $m/im$ is flat over $r/i$,. Criteria For Flatness.
From werk24.io
Tolerances IT Grades, General Tolerances Criteria For Flatness In this section we discuss criteria for flatness. Flatness is really an algebraic notion with a subtle geometric interpretation. Let $(r, p)$ be a local ring. If $\text{tor}_1^ r(m, r/i) = 0$ and $m/im$ is flat over $r/i$, then $m$ is flat over $r$. A very important class of results, namely criteria for flatness, are discussed in algebra, sections 10.99,. Criteria For Flatness.
From www.inradoptics.com
Guidelines to Metal Optics Roughness and Flatness Criteria For Flatness Flatness criteria help determine when a module is flat, including the tensor product and local flatness criteria. Flatness is really an algebraic notion with a subtle geometric interpretation. By lemma 10.99.8 we see that. A very important class of results, namely criteria for flatness, are discussed in algebra, sections 10.99, 10.101, 10.128, and more on morphisms,. Let $(r, p)$ be. Criteria For Flatness.
From bbs.homeshopmachinist.net
Flatness criteria for surface plates. The Home Shop Machinist Criteria For Flatness Flatness criteria help determine when a module is flat, including the tensor product and local flatness criteria. Flatness is really an algebraic notion with a subtle geometric interpretation. By lemma 10.99.8 we see that. If $\text{tor}_1^ r(m, r/i) = 0$ and $m/im$ is flat over $r/i$, then $m$ is flat over $r$. The main result in this section is lazard's. Criteria For Flatness.
From www.researchgate.net
Straightness and flatness rail tolerances [4]. Download Scientific Criteria For Flatness By lemma 10.99.8 we see that. In this section we discuss criteria for flatness. It is best explained in terms of modules and illustrated by. Flatness is really an algebraic notion with a subtle geometric interpretation. Let $(r, p)$ be a local ring. Flatness criteria help determine when a module is flat, including the tensor product and local flatness criteria.. Criteria For Flatness.
From viewfloor.co
How To Check Floor For Flatness Viewfloor.co Criteria For Flatness By lemma 10.99.8 we see that. The main result in this section is lazard's theorem (theorem 10.81.4 below), which says. Flatness criteria help determine when a module is flat, including the tensor product and local flatness criteria. If $m$ is a finitely presented module, then $m$ is flat iff $\mathrm{tor}_{1}^r(m,r/p)=0$. Let $(r, p)$ be a local ring. It is best. Criteria For Flatness.
From www.fullyinstrumented.com
Surface Plate What is It?, Materials, Grades, Dimension Standard, etc Criteria For Flatness If $\text{tor}_1^ r(m, r/i) = 0$ and $m/im$ is flat over $r/i$, then $m$ is flat over $r$. Let $(r, p)$ be a local ring. Flatness criteria help determine when a module is flat, including the tensor product and local flatness criteria. In this section we discuss criteria for flatness. If $m$ is a finitely presented module, then $m$ is. Criteria For Flatness.
From courses.skill-lync.com
What are Flatness and Parallelism? gdt flatness Criteria For Flatness By lemma 10.99.8 we see that. Flatness is really an algebraic notion with a subtle geometric interpretation. In this section we discuss criteria for flatness. It is best explained in terms of modules and illustrated by. Flatness criteria help determine when a module is flat, including the tensor product and local flatness criteria. The main result in this section is. Criteria For Flatness.
From mungfali.com
ASTM Flatness Tolerances Chart Criteria For Flatness Flatness criteria help determine when a module is flat, including the tensor product and local flatness criteria. The main result in this section is lazard's theorem (theorem 10.81.4 below), which says. If $m$ is a finitely presented module, then $m$ is flat iff $\mathrm{tor}_{1}^r(m,r/p)=0$. A very important class of results, namely criteria for flatness, are discussed in algebra, sections 10.99,. Criteria For Flatness.
From cinvex.us
Concrete Floor Flatness Standards Flooring Guide by Cinvex Criteria For Flatness Flatness criteria help determine when a module is flat, including the tensor product and local flatness criteria. If $m$ is a finitely presented module, then $m$ is flat iff $\mathrm{tor}_{1}^r(m,r/p)=0$. By lemma 10.99.8 we see that. If $\text{tor}_1^ r(m, r/i) = 0$ and $m/im$ is flat over $r/i$, then $m$ is flat over $r$. A very important class of results,. Criteria For Flatness.
From www.researchgate.net
(PDF) Calculation criteria for road pavement evenness. Part 1 Criteria For Flatness Flatness is really an algebraic notion with a subtle geometric interpretation. In this section we discuss criteria for flatness. Flatness criteria help determine when a module is flat, including the tensor product and local flatness criteria. It is best explained in terms of modules and illustrated by. By lemma 10.99.8 we see that. Let $(r, p)$ be a local ring.. Criteria For Flatness.
From bbs.homeshopmachinist.net
Flatness criteria for surface plates. The Home Shop Machinist Criteria For Flatness Flatness criteria help determine when a module is flat, including the tensor product and local flatness criteria. A very important class of results, namely criteria for flatness, are discussed in algebra, sections 10.99, 10.101, 10.128, and more on morphisms,. Let $(r, p)$ be a local ring. If $\text{tor}_1^ r(m, r/i) = 0$ and $m/im$ is flat over $r/i$, then $m$. Criteria For Flatness.
From mungfali.com
Flatness Tolerance Chart Criteria For Flatness It is best explained in terms of modules and illustrated by. Flatness criteria help determine when a module is flat, including the tensor product and local flatness criteria. Flatness is really an algebraic notion with a subtle geometric interpretation. A very important class of results, namely criteria for flatness, are discussed in algebra, sections 10.99, 10.101, 10.128, and more on. Criteria For Flatness.
From www.team-mfg.com
The Guide Of Flatness In GD&T TEAM MFG Criteria For Flatness Flatness is really an algebraic notion with a subtle geometric interpretation. If $m$ is a finitely presented module, then $m$ is flat iff $\mathrm{tor}_{1}^r(m,r/p)=0$. The main result in this section is lazard's theorem (theorem 10.81.4 below), which says. In this section we discuss criteria for flatness. By lemma 10.99.8 we see that. If $\text{tor}_1^ r(m, r/i) = 0$ and $m/im$. Criteria For Flatness.