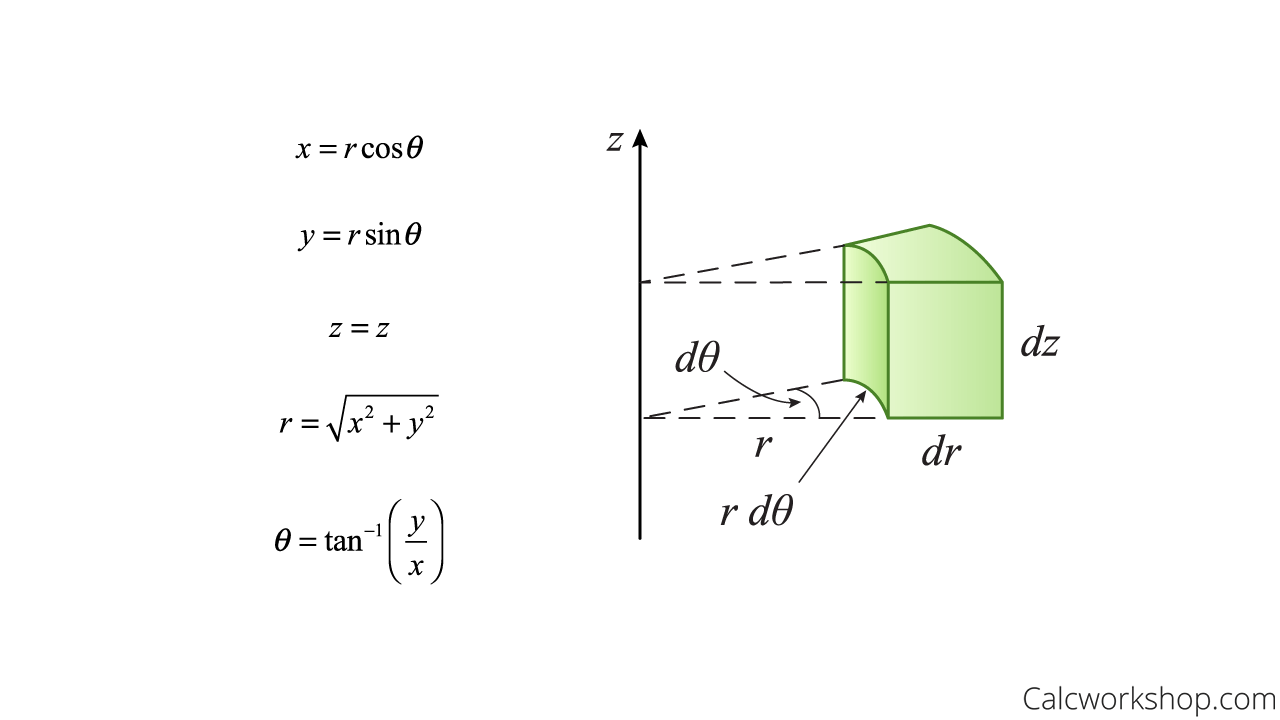
When To Use Spherical And Cylindrical Coordinates at Levi Sims blog

When To Use Spherical And Cylindrical Coordinates. Basically it makes things easier if your coordinates look like the problem. (15.6.2) ∫2π 0 ∫1 0 ∫ 4−r2√ − 4−r2√ r3cos2(θ)dzdrdθ= ∫2π 0 ∫1 0 2 4 −r2−. So, in cartesian coordinates we get x = ρ sin φ cos θ y = ρ sin φ sin θ z = ρ cos φ. If you have a problem with spherical symmetry, like the. As the name suggests, cylindrical coordinates are useful for dealing with problems involving cylinders, such as calculating the volume of a. We will first look at cylindrical coordinates. The locus z = a represents a sphere of radius a, and for this. We set this up in cylindrical coordinates, recalling that x = rcosθ: Spherical and cylindrical coordinates are two generalizations of polar coordinates to three dimensions. So, how do we convert back and forth from rectangular coordinates to spherical coordinates or from cylindrical coordinates to spherical coordinates? Spherical coordinates use rho (ρ ρ) as the distance between the origin and the point, whereas for cylindrical points, r r is the distance from the origin to the projection of the.

So, how do we convert back and forth from rectangular coordinates to spherical coordinates or from cylindrical coordinates to spherical coordinates? Basically it makes things easier if your coordinates look like the problem. Spherical and cylindrical coordinates are two generalizations of polar coordinates to three dimensions. The locus z = a represents a sphere of radius a, and for this. If you have a problem with spherical symmetry, like the. We will first look at cylindrical coordinates. We set this up in cylindrical coordinates, recalling that x = rcosθ: So, in cartesian coordinates we get x = ρ sin φ cos θ y = ρ sin φ sin θ z = ρ cos φ. (15.6.2) ∫2π 0 ∫1 0 ∫ 4−r2√ − 4−r2√ r3cos2(θ)dzdrdθ= ∫2π 0 ∫1 0 2 4 −r2−. As the name suggests, cylindrical coordinates are useful for dealing with problems involving cylinders, such as calculating the volume of a.

Cylindrical Coordinates Integral

When To Use Spherical And Cylindrical Coordinates So, in cartesian coordinates we get x = ρ sin φ cos θ y = ρ sin φ sin θ z = ρ cos φ. We will first look at cylindrical coordinates. So, in cartesian coordinates we get x = ρ sin φ cos θ y = ρ sin φ sin θ z = ρ cos φ. The locus z = a represents a sphere of radius a, and for this. As the name suggests, cylindrical coordinates are useful for dealing with problems involving cylinders, such as calculating the volume of a. (15.6.2) ∫2π 0 ∫1 0 ∫ 4−r2√ − 4−r2√ r3cos2(θ)dzdrdθ= ∫2π 0 ∫1 0 2 4 −r2−. We set this up in cylindrical coordinates, recalling that x = rcosθ: So, how do we convert back and forth from rectangular coordinates to spherical coordinates or from cylindrical coordinates to spherical coordinates? If you have a problem with spherical symmetry, like the. Spherical and cylindrical coordinates are two generalizations of polar coordinates to three dimensions. Spherical coordinates use rho (ρ ρ) as the distance between the origin and the point, whereas for cylindrical points, r r is the distance from the origin to the projection of the. Basically it makes things easier if your coordinates look like the problem.