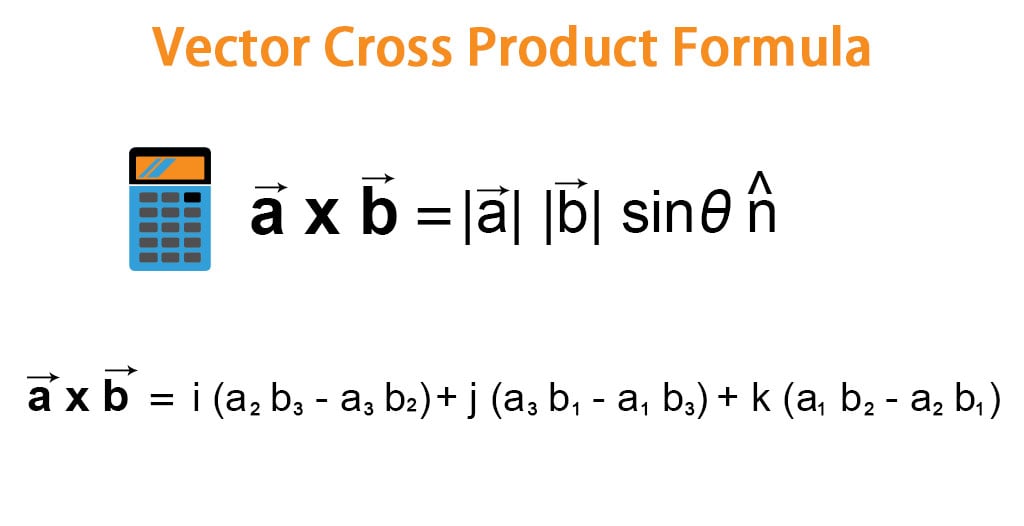Cross Product In Mathematica . vectors in the wolfram language can always mix numbers and arbitrary symbolic or algebraic elements. in this section, we develop an operation called the cross product, which allows us to find a vector orthogonal to. crossproduct [v 1, v 2, coordsys] is computed by converting v 1 and v 2 to cartesian coordinates, forming the cross. $\begingroup$ cross product of two vectors gives a vector orthogonal to them. define the tangent, normal and binormal vectors in terms of cross products of the first two derivatives: in linear algebra, a cross is defined as a set of n mutually perpendicular pairs of vectors of equal magnitude from a. If you have two 2d vectors, they are. For vectors and in , the cross product in is defined by.
from www.educba.com
If you have two 2d vectors, they are. in linear algebra, a cross is defined as a set of n mutually perpendicular pairs of vectors of equal magnitude from a. $\begingroup$ cross product of two vectors gives a vector orthogonal to them. define the tangent, normal and binormal vectors in terms of cross products of the first two derivatives: vectors in the wolfram language can always mix numbers and arbitrary symbolic or algebraic elements. For vectors and in , the cross product in is defined by. crossproduct [v 1, v 2, coordsys] is computed by converting v 1 and v 2 to cartesian coordinates, forming the cross. in this section, we develop an operation called the cross product, which allows us to find a vector orthogonal to.
Vector Cross Product Formula Examples with Excel Template
Cross Product In Mathematica $\begingroup$ cross product of two vectors gives a vector orthogonal to them. crossproduct [v 1, v 2, coordsys] is computed by converting v 1 and v 2 to cartesian coordinates, forming the cross. vectors in the wolfram language can always mix numbers and arbitrary symbolic or algebraic elements. in this section, we develop an operation called the cross product, which allows us to find a vector orthogonal to. in linear algebra, a cross is defined as a set of n mutually perpendicular pairs of vectors of equal magnitude from a. For vectors and in , the cross product in is defined by. If you have two 2d vectors, they are. $\begingroup$ cross product of two vectors gives a vector orthogonal to them. define the tangent, normal and binormal vectors in terms of cross products of the first two derivatives:
From en.wikipedia.org
Cross product Wikipedia Cross Product In Mathematica If you have two 2d vectors, they are. define the tangent, normal and binormal vectors in terms of cross products of the first two derivatives: in linear algebra, a cross is defined as a set of n mutually perpendicular pairs of vectors of equal magnitude from a. $\begingroup$ cross product of two vectors gives a vector orthogonal. Cross Product In Mathematica.
From www.askpython.com
Numpy Cross Product A Complete Guide AskPython Cross Product In Mathematica in linear algebra, a cross is defined as a set of n mutually perpendicular pairs of vectors of equal magnitude from a. If you have two 2d vectors, they are. For vectors and in , the cross product in is defined by. define the tangent, normal and binormal vectors in terms of cross products of the first two. Cross Product In Mathematica.
From www.youtube.com
What is the CROSS PRODUCT and how to find the cross product of two Cross Product In Mathematica define the tangent, normal and binormal vectors in terms of cross products of the first two derivatives: in linear algebra, a cross is defined as a set of n mutually perpendicular pairs of vectors of equal magnitude from a. in this section, we develop an operation called the cross product, which allows us to find a vector. Cross Product In Mathematica.
From www.slideserve.com
PPT The Cross Product PowerPoint Presentation, free download ID3195487 Cross Product In Mathematica in linear algebra, a cross is defined as a set of n mutually perpendicular pairs of vectors of equal magnitude from a. $\begingroup$ cross product of two vectors gives a vector orthogonal to them. If you have two 2d vectors, they are. crossproduct [v 1, v 2, coordsys] is computed by converting v 1 and v 2. Cross Product In Mathematica.
From giasutamtaiduc.com
Cross Product Formula ⭐️⭐️⭐️⭐️⭐ Cross Product In Mathematica vectors in the wolfram language can always mix numbers and arbitrary symbolic or algebraic elements. $\begingroup$ cross product of two vectors gives a vector orthogonal to them. If you have two 2d vectors, they are. define the tangent, normal and binormal vectors in terms of cross products of the first two derivatives: in linear algebra, a. Cross Product In Mathematica.
From calcworkshop.com
Cross Product for Calculus Everything You Need to Know Cross Product In Mathematica in this section, we develop an operation called the cross product, which allows us to find a vector orthogonal to. define the tangent, normal and binormal vectors in terms of cross products of the first two derivatives: vectors in the wolfram language can always mix numbers and arbitrary symbolic or algebraic elements. $\begingroup$ cross product of. Cross Product In Mathematica.
From firmfunda.com
Vector Algebra Cross Product First Principles Cross Product In Mathematica crossproduct [v 1, v 2, coordsys] is computed by converting v 1 and v 2 to cartesian coordinates, forming the cross. If you have two 2d vectors, they are. define the tangent, normal and binormal vectors in terms of cross products of the first two derivatives: in this section, we develop an operation called the cross product,. Cross Product In Mathematica.
From www.youtube.com
Math and Dynamics Vector Cross Product as MatrixVector Multiplication Cross Product In Mathematica vectors in the wolfram language can always mix numbers and arbitrary symbolic or algebraic elements. $\begingroup$ cross product of two vectors gives a vector orthogonal to them. If you have two 2d vectors, they are. For vectors and in , the cross product in is defined by. define the tangent, normal and binormal vectors in terms of. Cross Product In Mathematica.
From www.pearson.com
Cross product, determinant method Pearson+ Channels Cross Product In Mathematica $\begingroup$ cross product of two vectors gives a vector orthogonal to them. in linear algebra, a cross is defined as a set of n mutually perpendicular pairs of vectors of equal magnitude from a. vectors in the wolfram language can always mix numbers and arbitrary symbolic or algebraic elements. crossproduct [v 1, v 2, coordsys] is. Cross Product In Mathematica.
From www.slideshare.net
Lesson 3 The Cross Product Cross Product In Mathematica $\begingroup$ cross product of two vectors gives a vector orthogonal to them. vectors in the wolfram language can always mix numbers and arbitrary symbolic or algebraic elements. If you have two 2d vectors, they are. crossproduct [v 1, v 2, coordsys] is computed by converting v 1 and v 2 to cartesian coordinates, forming the cross. . Cross Product In Mathematica.
From www.slideserve.com
PPT Cross Product PowerPoint Presentation, free download ID395792 Cross Product In Mathematica in linear algebra, a cross is defined as a set of n mutually perpendicular pairs of vectors of equal magnitude from a. in this section, we develop an operation called the cross product, which allows us to find a vector orthogonal to. vectors in the wolfram language can always mix numbers and arbitrary symbolic or algebraic elements.. Cross Product In Mathematica.
From www.slideserve.com
PPT Cross Product PowerPoint Presentation, free download ID2849156 Cross Product In Mathematica $\begingroup$ cross product of two vectors gives a vector orthogonal to them. define the tangent, normal and binormal vectors in terms of cross products of the first two derivatives: For vectors and in , the cross product in is defined by. in linear algebra, a cross is defined as a set of n mutually perpendicular pairs of. Cross Product In Mathematica.
From www.youtube.com
(Calculus 3) Cross product basic idea, determinants, and a first Cross Product In Mathematica vectors in the wolfram language can always mix numbers and arbitrary symbolic or algebraic elements. For vectors and in , the cross product in is defined by. in this section, we develop an operation called the cross product, which allows us to find a vector orthogonal to. crossproduct [v 1, v 2, coordsys] is computed by converting. Cross Product In Mathematica.
From guzintamath.com
The Cross Product Guzinta Math Cross Product In Mathematica For vectors and in , the cross product in is defined by. define the tangent, normal and binormal vectors in terms of cross products of the first two derivatives: crossproduct [v 1, v 2, coordsys] is computed by converting v 1 and v 2 to cartesian coordinates, forming the cross. in linear algebra, a cross is defined. Cross Product In Mathematica.
From study.com
Cross Product Method Definition, Rules & Properties Lesson Cross Product In Mathematica in linear algebra, a cross is defined as a set of n mutually perpendicular pairs of vectors of equal magnitude from a. crossproduct [v 1, v 2, coordsys] is computed by converting v 1 and v 2 to cartesian coordinates, forming the cross. If you have two 2d vectors, they are. $\begingroup$ cross product of two vectors. Cross Product In Mathematica.
From www.yumpu.com
Cross (vector) product of two vectors Cross Product In Mathematica $\begingroup$ cross product of two vectors gives a vector orthogonal to them. vectors in the wolfram language can always mix numbers and arbitrary symbolic or algebraic elements. If you have two 2d vectors, they are. in this section, we develop an operation called the cross product, which allows us to find a vector orthogonal to. crossproduct. Cross Product In Mathematica.
From www.youtube.com
Cross Product of two Vectors Right hand Rule Math Dot Com YouTube Cross Product In Mathematica vectors in the wolfram language can always mix numbers and arbitrary symbolic or algebraic elements. For vectors and in , the cross product in is defined by. crossproduct [v 1, v 2, coordsys] is computed by converting v 1 and v 2 to cartesian coordinates, forming the cross. in this section, we develop an operation called the. Cross Product In Mathematica.
From www.youtube.com
Very easy way to calculate the cross product Linear Algebra YouTube Cross Product In Mathematica in linear algebra, a cross is defined as a set of n mutually perpendicular pairs of vectors of equal magnitude from a. vectors in the wolfram language can always mix numbers and arbitrary symbolic or algebraic elements. If you have two 2d vectors, they are. define the tangent, normal and binormal vectors in terms of cross products. Cross Product In Mathematica.
From www.pinterest.com
Properties of the Cross Product Vector Triple Product in 2023 Cross Product In Mathematica For vectors and in , the cross product in is defined by. $\begingroup$ cross product of two vectors gives a vector orthogonal to them. vectors in the wolfram language can always mix numbers and arbitrary symbolic or algebraic elements. in this section, we develop an operation called the cross product, which allows us to find a vector. Cross Product In Mathematica.
From firmfunda.com
Vector Algebra Cross Product First Principles Cross Product In Mathematica define the tangent, normal and binormal vectors in terms of cross products of the first two derivatives: crossproduct [v 1, v 2, coordsys] is computed by converting v 1 and v 2 to cartesian coordinates, forming the cross. in linear algebra, a cross is defined as a set of n mutually perpendicular pairs of vectors of equal. Cross Product In Mathematica.
From www.cuemath.com
Cross Product Cuemath Cross Product In Mathematica crossproduct [v 1, v 2, coordsys] is computed by converting v 1 and v 2 to cartesian coordinates, forming the cross. $\begingroup$ cross product of two vectors gives a vector orthogonal to them. in this section, we develop an operation called the cross product, which allows us to find a vector orthogonal to. define the tangent,. Cross Product In Mathematica.
From www.educba.com
Vector Cross Product Formula Examples with Excel Template Cross Product In Mathematica in this section, we develop an operation called the cross product, which allows us to find a vector orthogonal to. vectors in the wolfram language can always mix numbers and arbitrary symbolic or algebraic elements. If you have two 2d vectors, they are. define the tangent, normal and binormal vectors in terms of cross products of the. Cross Product In Mathematica.
From www.cuemath.com
Cross Product of Two Vectors Definition, Formula, Examples Cross Product In Mathematica For vectors and in , the cross product in is defined by. vectors in the wolfram language can always mix numbers and arbitrary symbolic or algebraic elements. If you have two 2d vectors, they are. crossproduct [v 1, v 2, coordsys] is computed by converting v 1 and v 2 to cartesian coordinates, forming the cross. in. Cross Product In Mathematica.
From www.showme.com
Cross Product and its Properties Math, Calculus, Cross products ShowMe Cross Product In Mathematica crossproduct [v 1, v 2, coordsys] is computed by converting v 1 and v 2 to cartesian coordinates, forming the cross. in linear algebra, a cross is defined as a set of n mutually perpendicular pairs of vectors of equal magnitude from a. define the tangent, normal and binormal vectors in terms of cross products of the. Cross Product In Mathematica.
From www.youtube.com
The Cross Product in Determinant Form YouTube Cross Product In Mathematica define the tangent, normal and binormal vectors in terms of cross products of the first two derivatives: vectors in the wolfram language can always mix numbers and arbitrary symbolic or algebraic elements. in this section, we develop an operation called the cross product, which allows us to find a vector orthogonal to. If you have two 2d. Cross Product In Mathematica.
From www.youtube.com
Cross Product of Two 3 by 3 Vectors (Linear Algebra) YouTube Cross Product In Mathematica For vectors and in , the cross product in is defined by. crossproduct [v 1, v 2, coordsys] is computed by converting v 1 and v 2 to cartesian coordinates, forming the cross. define the tangent, normal and binormal vectors in terms of cross products of the first two derivatives: in this section, we develop an operation. Cross Product In Mathematica.
From www.slideserve.com
PPT Cross Product PowerPoint Presentation, free download ID9402769 Cross Product In Mathematica If you have two 2d vectors, they are. $\begingroup$ cross product of two vectors gives a vector orthogonal to them. in this section, we develop an operation called the cross product, which allows us to find a vector orthogonal to. vectors in the wolfram language can always mix numbers and arbitrary symbolic or algebraic elements. define. Cross Product In Mathematica.
From www.youtube.com
Lesson7 Vector (Cross Product of Vectors, Cross Product of Unit Cross Product In Mathematica vectors in the wolfram language can always mix numbers and arbitrary symbolic or algebraic elements. in linear algebra, a cross is defined as a set of n mutually perpendicular pairs of vectors of equal magnitude from a. define the tangent, normal and binormal vectors in terms of cross products of the first two derivatives: For vectors and. Cross Product In Mathematica.
From www.youtube.com
The Cross Product Definition and Derivation YouTube Cross Product In Mathematica vectors in the wolfram language can always mix numbers and arbitrary symbolic or algebraic elements. crossproduct [v 1, v 2, coordsys] is computed by converting v 1 and v 2 to cartesian coordinates, forming the cross. in linear algebra, a cross is defined as a set of n mutually perpendicular pairs of vectors of equal magnitude from. Cross Product In Mathematica.
From giasutamtaiduc.com
Cross Product Formula ⭐️⭐️⭐️⭐️⭐ Cross Product In Mathematica in linear algebra, a cross is defined as a set of n mutually perpendicular pairs of vectors of equal magnitude from a. $\begingroup$ cross product of two vectors gives a vector orthogonal to them. define the tangent, normal and binormal vectors in terms of cross products of the first two derivatives: in this section, we develop. Cross Product In Mathematica.
From giasutamtaiduc.com
Cross Product Formula ⭐️⭐️⭐️⭐️⭐ Cross Product In Mathematica For vectors and in , the cross product in is defined by. crossproduct [v 1, v 2, coordsys] is computed by converting v 1 and v 2 to cartesian coordinates, forming the cross. If you have two 2d vectors, they are. in this section, we develop an operation called the cross product, which allows us to find a. Cross Product In Mathematica.
From www.youtube.com
Cross product of vectors Determinant method vs the direct calculation Cross Product In Mathematica vectors in the wolfram language can always mix numbers and arbitrary symbolic or algebraic elements. crossproduct [v 1, v 2, coordsys] is computed by converting v 1 and v 2 to cartesian coordinates, forming the cross. in linear algebra, a cross is defined as a set of n mutually perpendicular pairs of vectors of equal magnitude from. Cross Product In Mathematica.
From oldeenglishconsortium.org
Cross products Chapter 10, Essence of linear algebra เนื้อหาที่ Cross Product In Mathematica vectors in the wolfram language can always mix numbers and arbitrary symbolic or algebraic elements. in this section, we develop an operation called the cross product, which allows us to find a vector orthogonal to. For vectors and in , the cross product in is defined by. $\begingroup$ cross product of two vectors gives a vector orthogonal. Cross Product In Mathematica.
From dutchvica.weebly.com
Crossproduct mathematica 113 dutchvica Cross Product In Mathematica crossproduct [v 1, v 2, coordsys] is computed by converting v 1 and v 2 to cartesian coordinates, forming the cross. vectors in the wolfram language can always mix numbers and arbitrary symbolic or algebraic elements. in linear algebra, a cross is defined as a set of n mutually perpendicular pairs of vectors of equal magnitude from. Cross Product In Mathematica.
From www.youtube.com
Properties of the Cross Product YouTube Cross Product In Mathematica in this section, we develop an operation called the cross product, which allows us to find a vector orthogonal to. $\begingroup$ cross product of two vectors gives a vector orthogonal to them. For vectors and in , the cross product in is defined by. define the tangent, normal and binormal vectors in terms of cross products of. Cross Product In Mathematica.