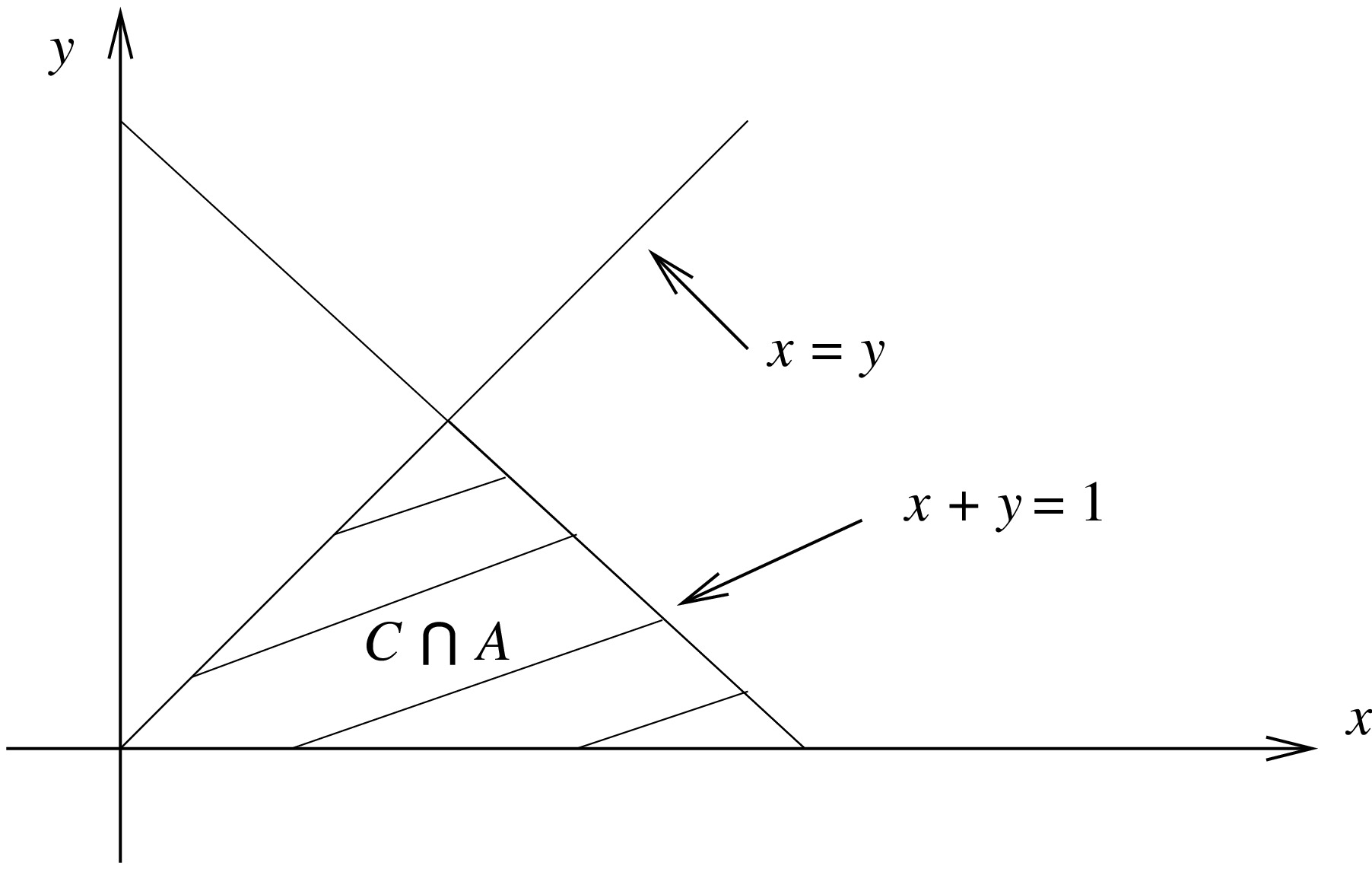
Joint Generating Function . (using a vector notation at the end). Moment generating functions are a neat mathematical trick which sometimes sidesteps these tedious calculations. Explain and apply joint moment generating functions. Let $(x,y)$ be a continues bivariate r.v. We can derive moments of most distributions by evaluating probability. Find the moment generating function of x+ y and the moment generating function of x y. One way to get around this, at the cost of considerable work, is to use the characteristic function ’ x(t) =. One problem with the moment generating function is that it might be in nite. Consider the random quantities x+ y and x y. Their joint moment generating function is.
from bookdown.org
Let $(x,y)$ be a continues bivariate r.v. One way to get around this, at the cost of considerable work, is to use the characteristic function ’ x(t) =. Consider the random quantities x+ y and x y. One problem with the moment generating function is that it might be in nite. Moment generating functions are a neat mathematical trick which sometimes sidesteps these tedious calculations. Explain and apply joint moment generating functions. We can derive moments of most distributions by evaluating probability. (using a vector notation at the end). Find the moment generating function of x+ y and the moment generating function of x y. Their joint moment generating function is.
Chapter 6 Joint Distribution Functions Foundations of Statistics
Joint Generating Function We can derive moments of most distributions by evaluating probability. One way to get around this, at the cost of considerable work, is to use the characteristic function ’ x(t) =. Consider the random quantities x+ y and x y. (using a vector notation at the end). Explain and apply joint moment generating functions. Let $(x,y)$ be a continues bivariate r.v. Moment generating functions are a neat mathematical trick which sometimes sidesteps these tedious calculations. Their joint moment generating function is. We can derive moments of most distributions by evaluating probability. One problem with the moment generating function is that it might be in nite. Find the moment generating function of x+ y and the moment generating function of x y.
From bookdown.org
Chapter 6 Joint Distribution Functions Foundations of Statistics Joint Generating Function Explain and apply joint moment generating functions. One way to get around this, at the cost of considerable work, is to use the characteristic function ’ x(t) =. We can derive moments of most distributions by evaluating probability. One problem with the moment generating function is that it might be in nite. Find the moment generating function of x+ y. Joint Generating Function.
From www.scribd.com
Joint Moment Generating Function of R.V.'S and Equality in Distribution Joint Generating Function Their joint moment generating function is. Explain and apply joint moment generating functions. Find the moment generating function of x+ y and the moment generating function of x y. Let $(x,y)$ be a continues bivariate r.v. (using a vector notation at the end). Moment generating functions are a neat mathematical trick which sometimes sidesteps these tedious calculations. We can derive. Joint Generating Function.
From courses.lumenlearning.com
Classification of Joints Boundless Anatomy and Physiology Joint Generating Function (using a vector notation at the end). Their joint moment generating function is. We can derive moments of most distributions by evaluating probability. Consider the random quantities x+ y and x y. One problem with the moment generating function is that it might be in nite. Explain and apply joint moment generating functions. Find the moment generating function of x+. Joint Generating Function.
From trifocusfitnessacademy.co.za
What is the Function of a Joint? Joint Generating Function Consider the random quantities x+ y and x y. Find the moment generating function of x+ y and the moment generating function of x y. One way to get around this, at the cost of considerable work, is to use the characteristic function ’ x(t) =. We can derive moments of most distributions by evaluating probability. Explain and apply joint. Joint Generating Function.
From www.youtube.com
Joint moment generating function YouTube Joint Generating Function Explain and apply joint moment generating functions. One way to get around this, at the cost of considerable work, is to use the characteristic function ’ x(t) =. (using a vector notation at the end). Let $(x,y)$ be a continues bivariate r.v. We can derive moments of most distributions by evaluating probability. Find the moment generating function of x+ y. Joint Generating Function.
From ndupress.ndu.edu
Getting the Joint Functions Right > National Defense University Press Joint Generating Function One way to get around this, at the cost of considerable work, is to use the characteristic function ’ x(t) =. Moment generating functions are a neat mathematical trick which sometimes sidesteps these tedious calculations. Explain and apply joint moment generating functions. One problem with the moment generating function is that it might be in nite. Consider the random quantities. Joint Generating Function.
From www.youtube.com
Bivariate distributions; moment generating functions YouTube Joint Generating Function Explain and apply joint moment generating functions. We can derive moments of most distributions by evaluating probability. Find the moment generating function of x+ y and the moment generating function of x y. Consider the random quantities x+ y and x y. Their joint moment generating function is. (using a vector notation at the end). Moment generating functions are a. Joint Generating Function.
From www.researchgate.net
(PDF) Joint Probability Generating Function for Degrees of Active Joint Generating Function We can derive moments of most distributions by evaluating probability. Find the moment generating function of x+ y and the moment generating function of x y. Moment generating functions are a neat mathematical trick which sometimes sidesteps these tedious calculations. Consider the random quantities x+ y and x y. Their joint moment generating function is. (using a vector notation at. Joint Generating Function.
From slideplayer.com
PRODUCT MOMENTS OF BIVARIATE RANDOM VARIABLES ppt download Joint Generating Function Find the moment generating function of x+ y and the moment generating function of x y. (using a vector notation at the end). One problem with the moment generating function is that it might be in nite. Moment generating functions are a neat mathematical trick which sometimes sidesteps these tedious calculations. One way to get around this, at the cost. Joint Generating Function.
From www.youtube.com
JOINT MOMENT GENERATING FUNCTION (JMGF) Properties of Joint MGF YouTube Joint Generating Function One way to get around this, at the cost of considerable work, is to use the characteristic function ’ x(t) =. Consider the random quantities x+ y and x y. Moment generating functions are a neat mathematical trick which sometimes sidesteps these tedious calculations. Their joint moment generating function is. (using a vector notation at the end). One problem with. Joint Generating Function.
From www.numerade.com
SOLVED Let X and Y be two jointly normal variables with E(X) = a, E (Y Joint Generating Function We can derive moments of most distributions by evaluating probability. (using a vector notation at the end). Let $(x,y)$ be a continues bivariate r.v. Their joint moment generating function is. One way to get around this, at the cost of considerable work, is to use the characteristic function ’ x(t) =. Explain and apply joint moment generating functions. Moment generating. Joint Generating Function.
From www.youtube.com
Joint moment generating function and characteristic function continued Joint Generating Function (using a vector notation at the end). Let $(x,y)$ be a continues bivariate r.v. Their joint moment generating function is. Consider the random quantities x+ y and x y. Explain and apply joint moment generating functions. One problem with the moment generating function is that it might be in nite. Find the moment generating function of x+ y and the. Joint Generating Function.
From www.chegg.com
Solved Calculate the joint moment generating function of the Joint Generating Function Consider the random quantities x+ y and x y. Moment generating functions are a neat mathematical trick which sometimes sidesteps these tedious calculations. We can derive moments of most distributions by evaluating probability. (using a vector notation at the end). Explain and apply joint moment generating functions. Let $(x,y)$ be a continues bivariate r.v. One problem with the moment generating. Joint Generating Function.
From studylib.net
lesson 5 Joints structure and function Joint Generating Function Moment generating functions are a neat mathematical trick which sometimes sidesteps these tedious calculations. Explain and apply joint moment generating functions. One problem with the moment generating function is that it might be in nite. (using a vector notation at the end). One way to get around this, at the cost of considerable work, is to use the characteristic function. Joint Generating Function.
From www.researchgate.net
(PDF) Joint Moment Generating Function of Ages of Information in Networks Joint Generating Function One way to get around this, at the cost of considerable work, is to use the characteristic function ’ x(t) =. Explain and apply joint moment generating functions. Consider the random quantities x+ y and x y. We can derive moments of most distributions by evaluating probability. Moment generating functions are a neat mathematical trick which sometimes sidesteps these tedious. Joint Generating Function.
From www.slideserve.com
PPT Section 8 Joint, Marginal, and Conditional Distributions Joint Generating Function Explain and apply joint moment generating functions. (using a vector notation at the end). Their joint moment generating function is. Moment generating functions are a neat mathematical trick which sometimes sidesteps these tedious calculations. One way to get around this, at the cost of considerable work, is to use the characteristic function ’ x(t) =. Let $(x,y)$ be a continues. Joint Generating Function.
From www.youtube.com
Using the Joint Moment Generating Function to find an expected value Joint Generating Function We can derive moments of most distributions by evaluating probability. Find the moment generating function of x+ y and the moment generating function of x y. Explain and apply joint moment generating functions. One way to get around this, at the cost of considerable work, is to use the characteristic function ’ x(t) =. Let $(x,y)$ be a continues bivariate. Joint Generating Function.
From www.chegg.com
Solved X = (X_1 X_2 X_3) have have joint moment generating Joint Generating Function We can derive moments of most distributions by evaluating probability. Find the moment generating function of x+ y and the moment generating function of x y. Explain and apply joint moment generating functions. Moment generating functions are a neat mathematical trick which sometimes sidesteps these tedious calculations. One problem with the moment generating function is that it might be in. Joint Generating Function.
From www.researchgate.net
(PDF) Joint Moment Generating Functions of Nonadjacent Dual Generalized Joint Generating Function We can derive moments of most distributions by evaluating probability. Find the moment generating function of x+ y and the moment generating function of x y. Their joint moment generating function is. One problem with the moment generating function is that it might be in nite. Moment generating functions are a neat mathematical trick which sometimes sidesteps these tedious calculations.. Joint Generating Function.
From www.researchgate.net
(PDF) Joint MomentGenerating Function, Covariance, and Correlation Joint Generating Function Let $(x,y)$ be a continues bivariate r.v. Find the moment generating function of x+ y and the moment generating function of x y. Their joint moment generating function is. We can derive moments of most distributions by evaluating probability. Consider the random quantities x+ y and x y. Explain and apply joint moment generating functions. One way to get around. Joint Generating Function.
From www.pdhpe.net
Structure and function of synovial joints HSC PDHPE Joint Generating Function Their joint moment generating function is. One problem with the moment generating function is that it might be in nite. Explain and apply joint moment generating functions. Consider the random quantities x+ y and x y. (using a vector notation at the end). One way to get around this, at the cost of considerable work, is to use the characteristic. Joint Generating Function.
From www.slideserve.com
PPT Chapter 6 The Muscle Anatomy PowerPoint Presentation, free Joint Generating Function Their joint moment generating function is. Let $(x,y)$ be a continues bivariate r.v. Consider the random quantities x+ y and x y. One way to get around this, at the cost of considerable work, is to use the characteristic function ’ x(t) =. (using a vector notation at the end). One problem with the moment generating function is that it. Joint Generating Function.
From www.youtube.com
Joint moment generating functions YouTube Joint Generating Function Explain and apply joint moment generating functions. Their joint moment generating function is. We can derive moments of most distributions by evaluating probability. (using a vector notation at the end). One way to get around this, at the cost of considerable work, is to use the characteristic function ’ x(t) =. Consider the random quantities x+ y and x y.. Joint Generating Function.
From www.chegg.com
Solved EXERCISE 8 Let X = (X1,X2, X3) has joint moment Joint Generating Function Consider the random quantities x+ y and x y. Their joint moment generating function is. Find the moment generating function of x+ y and the moment generating function of x y. Explain and apply joint moment generating functions. Let $(x,y)$ be a continues bivariate r.v. One way to get around this, at the cost of considerable work, is to use. Joint Generating Function.
From www.youtube.com
Multivariate distributions Joint moment generating functions YouTube Joint Generating Function Consider the random quantities x+ y and x y. Their joint moment generating function is. One problem with the moment generating function is that it might be in nite. One way to get around this, at the cost of considerable work, is to use the characteristic function ’ x(t) =. Find the moment generating function of x+ y and the. Joint Generating Function.
From www.slideserve.com
PPT An Edgeworth Series Expansion for Multipath Fading Channel Joint Generating Function We can derive moments of most distributions by evaluating probability. Explain and apply joint moment generating functions. Find the moment generating function of x+ y and the moment generating function of x y. Moment generating functions are a neat mathematical trick which sometimes sidesteps these tedious calculations. One problem with the moment generating function is that it might be in. Joint Generating Function.
From www.researchgate.net
Integrated Model of Joint Function the mechanical components are Joint Generating Function Explain and apply joint moment generating functions. One way to get around this, at the cost of considerable work, is to use the characteristic function ’ x(t) =. Moment generating functions are a neat mathematical trick which sometimes sidesteps these tedious calculations. Let $(x,y)$ be a continues bivariate r.v. Consider the random quantities x+ y and x y. Their joint. Joint Generating Function.
From www.slideserve.com
PPT An Edgeworth Series Expansion for Multipath Fading Channel Joint Generating Function One way to get around this, at the cost of considerable work, is to use the characteristic function ’ x(t) =. One problem with the moment generating function is that it might be in nite. Their joint moment generating function is. Consider the random quantities x+ y and x y. (using a vector notation at the end). We can derive. Joint Generating Function.
From slideplayer.com
The distribution function F(x) ppt download Joint Generating Function Let $(x,y)$ be a continues bivariate r.v. We can derive moments of most distributions by evaluating probability. One way to get around this, at the cost of considerable work, is to use the characteristic function ’ x(t) =. Consider the random quantities x+ y and x y. Their joint moment generating function is. (using a vector notation at the end).. Joint Generating Function.
From www.slideserve.com
PPT Joints PowerPoint Presentation, free download ID2034256 Joint Generating Function We can derive moments of most distributions by evaluating probability. (using a vector notation at the end). One problem with the moment generating function is that it might be in nite. Let $(x,y)$ be a continues bivariate r.v. Explain and apply joint moment generating functions. Consider the random quantities x+ y and x y. Find the moment generating function of. Joint Generating Function.
From slideplayer.com
Chapter 3 Brownian Motion 洪敏誠 2009/07/31 / ppt download Joint Generating Function One problem with the moment generating function is that it might be in nite. We can derive moments of most distributions by evaluating probability. Consider the random quantities x+ y and x y. Moment generating functions are a neat mathematical trick which sometimes sidesteps these tedious calculations. Find the moment generating function of x+ y and the moment generating function. Joint Generating Function.
From www.chegg.com
Solved Calculate the joint moment generating function of the Joint Generating Function Let $(x,y)$ be a continues bivariate r.v. One way to get around this, at the cost of considerable work, is to use the characteristic function ’ x(t) =. One problem with the moment generating function is that it might be in nite. Consider the random quantities x+ y and x y. (using a vector notation at the end). Find the. Joint Generating Function.
From www.slideserve.com
PPT Joints PowerPoint Presentation ID529693 Joint Generating Function Their joint moment generating function is. Explain and apply joint moment generating functions. One way to get around this, at the cost of considerable work, is to use the characteristic function ’ x(t) =. One problem with the moment generating function is that it might be in nite. Let $(x,y)$ be a continues bivariate r.v. (using a vector notation at. Joint Generating Function.
From www.slideserve.com
PPT Brownian Motion PowerPoint Presentation, free download ID4492911 Joint Generating Function (using a vector notation at the end). Explain and apply joint moment generating functions. We can derive moments of most distributions by evaluating probability. Moment generating functions are a neat mathematical trick which sometimes sidesteps these tedious calculations. Their joint moment generating function is. One problem with the moment generating function is that it might be in nite. Let $(x,y)$. Joint Generating Function.
From virtualhomeschoolgroup.org
Study Notes Joint Generating Function One way to get around this, at the cost of considerable work, is to use the characteristic function ’ x(t) =. Find the moment generating function of x+ y and the moment generating function of x y. Their joint moment generating function is. Let $(x,y)$ be a continues bivariate r.v. Explain and apply joint moment generating functions. One problem with. Joint Generating Function.