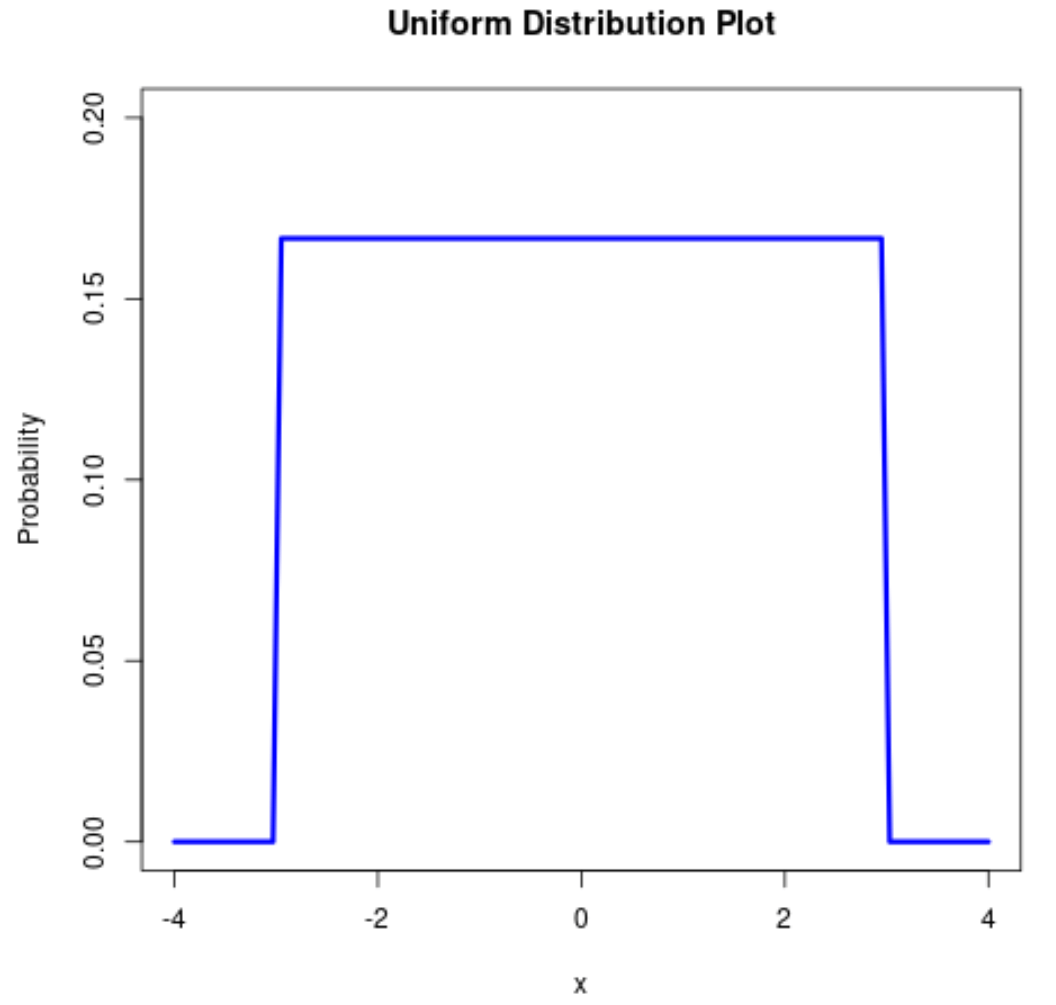
Density Function Of A Uniform Distribution . \(a\)= minimum \(b\) = maximum. The notation for the uniform distribution is \(x \sim u(a, b)\) where \(a =\) the lowest value of \(x\) and \(b =\) the highest. The two parameters that define the uniform distribution are: A continuous random variable \(x\) has a uniform distribution, denoted \(u(a,b)\), if its probability density function is:. The probability density function (pdf) of a continuous uniform distribution is defined as follows. In this section, we will introduce some important probability density functions and give some examples of their use. The probability density function is the constant function \(f(x) = 1/(b‐a)\),. The probability density function and cumulative distribution function for a continuous uniform distribution on the interval [a,b] are p(x). An example of a continuous uniform distribution is shown in the figure below.
from www.statology.org
A continuous random variable \(x\) has a uniform distribution, denoted \(u(a,b)\), if its probability density function is:. \(a\)= minimum \(b\) = maximum. The probability density function (pdf) of a continuous uniform distribution is defined as follows. In this section, we will introduce some important probability density functions and give some examples of their use. The probability density function and cumulative distribution function for a continuous uniform distribution on the interval [a,b] are p(x). The two parameters that define the uniform distribution are: An example of a continuous uniform distribution is shown in the figure below. The probability density function is the constant function \(f(x) = 1/(b‐a)\),. The notation for the uniform distribution is \(x \sim u(a, b)\) where \(a =\) the lowest value of \(x\) and \(b =\) the highest.
How to Plot a Uniform Distribution in R
Density Function Of A Uniform Distribution The two parameters that define the uniform distribution are: The probability density function is the constant function \(f(x) = 1/(b‐a)\),. In this section, we will introduce some important probability density functions and give some examples of their use. The two parameters that define the uniform distribution are: An example of a continuous uniform distribution is shown in the figure below. The probability density function (pdf) of a continuous uniform distribution is defined as follows. The notation for the uniform distribution is \(x \sim u(a, b)\) where \(a =\) the lowest value of \(x\) and \(b =\) the highest. The probability density function and cumulative distribution function for a continuous uniform distribution on the interval [a,b] are p(x). \(a\)= minimum \(b\) = maximum. A continuous random variable \(x\) has a uniform distribution, denoted \(u(a,b)\), if its probability density function is:.
From www.youtube.com
Uniform distribution moment generating function YouTube Density Function Of A Uniform Distribution An example of a continuous uniform distribution is shown in the figure below. A continuous random variable \(x\) has a uniform distribution, denoted \(u(a,b)\), if its probability density function is:. \(a\)= minimum \(b\) = maximum. The probability density function is the constant function \(f(x) = 1/(b‐a)\),. The probability density function (pdf) of a continuous uniform distribution is defined as follows.. Density Function Of A Uniform Distribution.
From www.youtube.com
Cumulative Distribution Functions and Probability Density Functions Density Function Of A Uniform Distribution The probability density function and cumulative distribution function for a continuous uniform distribution on the interval [a,b] are p(x). \(a\)= minimum \(b\) = maximum. The notation for the uniform distribution is \(x \sim u(a, b)\) where \(a =\) the lowest value of \(x\) and \(b =\) the highest. The two parameters that define the uniform distribution are: A continuous random. Density Function Of A Uniform Distribution.
From joiipweam.blob.core.windows.net
Likelihood Function Of A Uniform Distribution at Steven Phillips blog Density Function Of A Uniform Distribution A continuous random variable \(x\) has a uniform distribution, denoted \(u(a,b)\), if its probability density function is:. The probability density function (pdf) of a continuous uniform distribution is defined as follows. \(a\)= minimum \(b\) = maximum. The probability density function and cumulative distribution function for a continuous uniform distribution on the interval [a,b] are p(x). The probability density function is. Density Function Of A Uniform Distribution.
From deepai.org
Cumulative Distribution Function Definition DeepAI Density Function Of A Uniform Distribution An example of a continuous uniform distribution is shown in the figure below. \(a\)= minimum \(b\) = maximum. The probability density function and cumulative distribution function for a continuous uniform distribution on the interval [a,b] are p(x). The probability density function is the constant function \(f(x) = 1/(b‐a)\),. The probability density function (pdf) of a continuous uniform distribution is defined. Density Function Of A Uniform Distribution.
From www.researchgate.net
2 Density Functions of Normal Distribution Download Scientific Diagram Density Function Of A Uniform Distribution An example of a continuous uniform distribution is shown in the figure below. The probability density function is the constant function \(f(x) = 1/(b‐a)\),. A continuous random variable \(x\) has a uniform distribution, denoted \(u(a,b)\), if its probability density function is:. The probability density function (pdf) of a continuous uniform distribution is defined as follows. In this section, we will. Density Function Of A Uniform Distribution.
From www.cuemath.com
Uniform Distribution Formula Learn the Uniform Distribution Formula Density Function Of A Uniform Distribution The two parameters that define the uniform distribution are: The notation for the uniform distribution is \(x \sim u(a, b)\) where \(a =\) the lowest value of \(x\) and \(b =\) the highest. \(a\)= minimum \(b\) = maximum. The probability density function and cumulative distribution function for a continuous uniform distribution on the interval [a,b] are p(x). An example of. Density Function Of A Uniform Distribution.
From calcworkshop.com
Continuous Uniform Distribution (Defined w/ 5 Examples!) Density Function Of A Uniform Distribution The notation for the uniform distribution is \(x \sim u(a, b)\) where \(a =\) the lowest value of \(x\) and \(b =\) the highest. In this section, we will introduce some important probability density functions and give some examples of their use. The probability density function is the constant function \(f(x) = 1/(b‐a)\),. \(a\)= minimum \(b\) = maximum. A continuous. Density Function Of A Uniform Distribution.
From stats.stackexchange.com
distributions Uniform Density Function Cross Validated Density Function Of A Uniform Distribution The probability density function and cumulative distribution function for a continuous uniform distribution on the interval [a,b] are p(x). A continuous random variable \(x\) has a uniform distribution, denoted \(u(a,b)\), if its probability density function is:. An example of a continuous uniform distribution is shown in the figure below. In this section, we will introduce some important probability density functions. Density Function Of A Uniform Distribution.
From www.youtube.com
Maximum Likelihood Estimator Uniform Distribution Clearly Explained Density Function Of A Uniform Distribution A continuous random variable \(x\) has a uniform distribution, denoted \(u(a,b)\), if its probability density function is:. In this section, we will introduce some important probability density functions and give some examples of their use. An example of a continuous uniform distribution is shown in the figure below. The probability density function is the constant function \(f(x) = 1/(b‐a)\),. The. Density Function Of A Uniform Distribution.
From www.youtube.com
Probability Density Functions YouTube Density Function Of A Uniform Distribution An example of a continuous uniform distribution is shown in the figure below. A continuous random variable \(x\) has a uniform distribution, denoted \(u(a,b)\), if its probability density function is:. The probability density function and cumulative distribution function for a continuous uniform distribution on the interval [a,b] are p(x). The notation for the uniform distribution is \(x \sim u(a, b)\). Density Function Of A Uniform Distribution.
From quantitative-probabilitydistribution.blogspot.com
Uniform Probability Distribution Function Research Topics Density Function Of A Uniform Distribution The probability density function (pdf) of a continuous uniform distribution is defined as follows. A continuous random variable \(x\) has a uniform distribution, denoted \(u(a,b)\), if its probability density function is:. The probability density function and cumulative distribution function for a continuous uniform distribution on the interval [a,b] are p(x). The probability density function is the constant function \(f(x) =. Density Function Of A Uniform Distribution.
From nadlercreent.blogspot.com
Continues Randome Variable Probability of a Specific Result Nadler Creent Density Function Of A Uniform Distribution The probability density function (pdf) of a continuous uniform distribution is defined as follows. A continuous random variable \(x\) has a uniform distribution, denoted \(u(a,b)\), if its probability density function is:. The two parameters that define the uniform distribution are: \(a\)= minimum \(b\) = maximum. An example of a continuous uniform distribution is shown in the figure below. The probability. Density Function Of A Uniform Distribution.
From analystprep.com
PDF of a Uniform Distribution CFA, FRM, and Actuarial Exams Study Notes Density Function Of A Uniform Distribution The probability density function (pdf) of a continuous uniform distribution is defined as follows. The probability density function is the constant function \(f(x) = 1/(b‐a)\),. The two parameters that define the uniform distribution are: \(a\)= minimum \(b\) = maximum. An example of a continuous uniform distribution is shown in the figure below. In this section, we will introduce some important. Density Function Of A Uniform Distribution.
From datasciencelk.com
Probability Density Function Data Science Learning Keystone Density Function Of A Uniform Distribution \(a\)= minimum \(b\) = maximum. In this section, we will introduce some important probability density functions and give some examples of their use. The two parameters that define the uniform distribution are: The probability density function is the constant function \(f(x) = 1/(b‐a)\),. The probability density function and cumulative distribution function for a continuous uniform distribution on the interval [a,b]. Density Function Of A Uniform Distribution.
From www.slideserve.com
PPT The Bernoulli distribution PowerPoint Presentation, free download Density Function Of A Uniform Distribution \(a\)= minimum \(b\) = maximum. In this section, we will introduce some important probability density functions and give some examples of their use. The notation for the uniform distribution is \(x \sim u(a, b)\) where \(a =\) the lowest value of \(x\) and \(b =\) the highest. The probability density function (pdf) of a continuous uniform distribution is defined as. Density Function Of A Uniform Distribution.
From www.slideserve.com
PPT Chapter 1 Examining Distributions PowerPoint Presentation, free Density Function Of A Uniform Distribution The probability density function is the constant function \(f(x) = 1/(b‐a)\),. The notation for the uniform distribution is \(x \sim u(a, b)\) where \(a =\) the lowest value of \(x\) and \(b =\) the highest. The probability density function (pdf) of a continuous uniform distribution is defined as follows. The probability density function and cumulative distribution function for a continuous. Density Function Of A Uniform Distribution.
From www.pdfprof.com
Probabilités et variances Density Function Of A Uniform Distribution The two parameters that define the uniform distribution are: The probability density function is the constant function \(f(x) = 1/(b‐a)\),. In this section, we will introduce some important probability density functions and give some examples of their use. The probability density function and cumulative distribution function for a continuous uniform distribution on the interval [a,b] are p(x). \(a\)= minimum \(b\). Density Function Of A Uniform Distribution.
From www.numerade.com
SOLVED Table Continuous Probability Distributions Probability Density Density Function Of A Uniform Distribution \(a\)= minimum \(b\) = maximum. The probability density function is the constant function \(f(x) = 1/(b‐a)\),. The probability density function (pdf) of a continuous uniform distribution is defined as follows. The probability density function and cumulative distribution function for a continuous uniform distribution on the interval [a,b] are p(x). A continuous random variable \(x\) has a uniform distribution, denoted \(u(a,b)\),. Density Function Of A Uniform Distribution.
From www.slideserve.com
PPT Continuous Random Variables & The Normal Probability Distribution Density Function Of A Uniform Distribution The two parameters that define the uniform distribution are: In this section, we will introduce some important probability density functions and give some examples of their use. The probability density function (pdf) of a continuous uniform distribution is defined as follows. A continuous random variable \(x\) has a uniform distribution, denoted \(u(a,b)\), if its probability density function is:. An example. Density Function Of A Uniform Distribution.
From www.statology.org
How to Plot a Uniform Distribution in R Density Function Of A Uniform Distribution The notation for the uniform distribution is \(x \sim u(a, b)\) where \(a =\) the lowest value of \(x\) and \(b =\) the highest. The probability density function and cumulative distribution function for a continuous uniform distribution on the interval [a,b] are p(x). An example of a continuous uniform distribution is shown in the figure below. In this section, we. Density Function Of A Uniform Distribution.
From www.youtube.com
4.6 Distribution and Density of a Sum of Random Variables YouTube Density Function Of A Uniform Distribution The probability density function is the constant function \(f(x) = 1/(b‐a)\),. A continuous random variable \(x\) has a uniform distribution, denoted \(u(a,b)\), if its probability density function is:. The probability density function (pdf) of a continuous uniform distribution is defined as follows. An example of a continuous uniform distribution is shown in the figure below. The two parameters that define. Density Function Of A Uniform Distribution.
From www.youtube.com
Uniform distribution cumulative distribution function YouTube Density Function Of A Uniform Distribution In this section, we will introduce some important probability density functions and give some examples of their use. The probability density function (pdf) of a continuous uniform distribution is defined as follows. The notation for the uniform distribution is \(x \sim u(a, b)\) where \(a =\) the lowest value of \(x\) and \(b =\) the highest. An example of a. Density Function Of A Uniform Distribution.
From www.researchgate.net
(PDF) Uniform Distribution as the Limiting Form of a Density Function Density Function Of A Uniform Distribution The probability density function is the constant function \(f(x) = 1/(b‐a)\),. A continuous random variable \(x\) has a uniform distribution, denoted \(u(a,b)\), if its probability density function is:. The notation for the uniform distribution is \(x \sim u(a, b)\) where \(a =\) the lowest value of \(x\) and \(b =\) the highest. The two parameters that define the uniform distribution. Density Function Of A Uniform Distribution.
From www.slideserve.com
PPT Continuous Probability Distributions PowerPoint Presentation Density Function Of A Uniform Distribution \(a\)= minimum \(b\) = maximum. The two parameters that define the uniform distribution are: The probability density function (pdf) of a continuous uniform distribution is defined as follows. The probability density function and cumulative distribution function for a continuous uniform distribution on the interval [a,b] are p(x). The notation for the uniform distribution is \(x \sim u(a, b)\) where \(a. Density Function Of A Uniform Distribution.
From www.youtube.com
Find the Distribution Function Given the Density Function YouTube Density Function Of A Uniform Distribution In this section, we will introduce some important probability density functions and give some examples of their use. \(a\)= minimum \(b\) = maximum. The probability density function and cumulative distribution function for a continuous uniform distribution on the interval [a,b] are p(x). The probability density function (pdf) of a continuous uniform distribution is defined as follows. An example of a. Density Function Of A Uniform Distribution.
From www.slideserve.com
PPT Continuous Probability Distributions Continuous Random Variables Density Function Of A Uniform Distribution The two parameters that define the uniform distribution are: The probability density function is the constant function \(f(x) = 1/(b‐a)\),. An example of a continuous uniform distribution is shown in the figure below. A continuous random variable \(x\) has a uniform distribution, denoted \(u(a,b)\), if its probability density function is:. \(a\)= minimum \(b\) = maximum. The probability density function and. Density Function Of A Uniform Distribution.
From www.statscodes.com
Continuous Uniform Distributions in R StatsCodes Density Function Of A Uniform Distribution In this section, we will introduce some important probability density functions and give some examples of their use. \(a\)= minimum \(b\) = maximum. A continuous random variable \(x\) has a uniform distribution, denoted \(u(a,b)\), if its probability density function is:. An example of a continuous uniform distribution is shown in the figure below. The probability density function is the constant. Density Function Of A Uniform Distribution.
From analystprep.com
Properties of Continuous Uniform Distribution AnalystPrep CFA® Exam Density Function Of A Uniform Distribution An example of a continuous uniform distribution is shown in the figure below. The probability density function (pdf) of a continuous uniform distribution is defined as follows. The two parameters that define the uniform distribution are: In this section, we will introduce some important probability density functions and give some examples of their use. The probability density function is the. Density Function Of A Uniform Distribution.
From vasttechno.weebly.com
Cdf of a uniform distribution vasttechno Density Function Of A Uniform Distribution The probability density function and cumulative distribution function for a continuous uniform distribution on the interval [a,b] are p(x). An example of a continuous uniform distribution is shown in the figure below. The probability density function is the constant function \(f(x) = 1/(b‐a)\),. The probability density function (pdf) of a continuous uniform distribution is defined as follows. The two parameters. Density Function Of A Uniform Distribution.
From www.slideserve.com
PPT Continuous Probability Distributions PowerPoint Presentation Density Function Of A Uniform Distribution An example of a continuous uniform distribution is shown in the figure below. A continuous random variable \(x\) has a uniform distribution, denoted \(u(a,b)\), if its probability density function is:. The probability density function and cumulative distribution function for a continuous uniform distribution on the interval [a,b] are p(x). The probability density function (pdf) of a continuous uniform distribution is. Density Function Of A Uniform Distribution.
From www.youtube.com
L08.7 Cumulative Distribution Functions YouTube Density Function Of A Uniform Distribution A continuous random variable \(x\) has a uniform distribution, denoted \(u(a,b)\), if its probability density function is:. In this section, we will introduce some important probability density functions and give some examples of their use. An example of a continuous uniform distribution is shown in the figure below. The probability density function (pdf) of a continuous uniform distribution is defined. Density Function Of A Uniform Distribution.
From tech-ai-math.medium.com
Bayes Classifiers in depth. Bayes Theorem, Hypothesis, Probability Density Function Of A Uniform Distribution The probability density function and cumulative distribution function for a continuous uniform distribution on the interval [a,b] are p(x). The notation for the uniform distribution is \(x \sim u(a, b)\) where \(a =\) the lowest value of \(x\) and \(b =\) the highest. An example of a continuous uniform distribution is shown in the figure below. The two parameters that. Density Function Of A Uniform Distribution.
From ai.plainenglish.io
Probability distributions used in machine learning (part 1) by Tech Density Function Of A Uniform Distribution The probability density function (pdf) of a continuous uniform distribution is defined as follows. A continuous random variable \(x\) has a uniform distribution, denoted \(u(a,b)\), if its probability density function is:. The notation for the uniform distribution is \(x \sim u(a, b)\) where \(a =\) the lowest value of \(x\) and \(b =\) the highest. An example of a continuous. Density Function Of A Uniform Distribution.
From www.numerade.com
SOLVEDA uniform distribution is a continuous probability distribution Density Function Of A Uniform Distribution \(a\)= minimum \(b\) = maximum. In this section, we will introduce some important probability density functions and give some examples of their use. The notation for the uniform distribution is \(x \sim u(a, b)\) where \(a =\) the lowest value of \(x\) and \(b =\) the highest. The probability density function (pdf) of a continuous uniform distribution is defined as. Density Function Of A Uniform Distribution.
From faculty.nps.edu
Chapter 8 Continuous Random Variables Introduction to Statistics and Density Function Of A Uniform Distribution In this section, we will introduce some important probability density functions and give some examples of their use. A continuous random variable \(x\) has a uniform distribution, denoted \(u(a,b)\), if its probability density function is:. The probability density function (pdf) of a continuous uniform distribution is defined as follows. \(a\)= minimum \(b\) = maximum. The probability density function and cumulative. Density Function Of A Uniform Distribution.