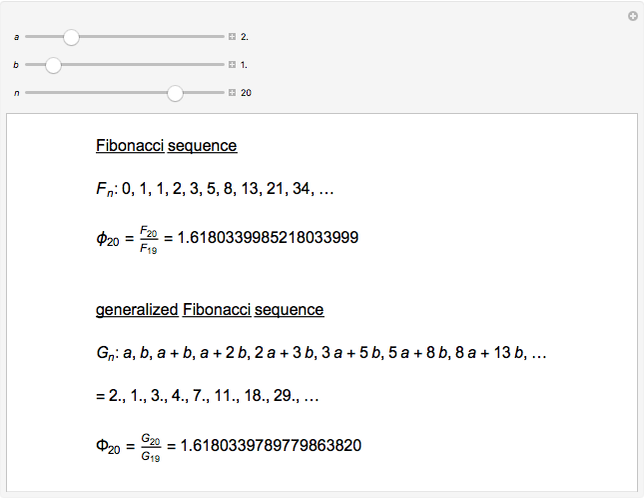
How Will We Determine Golden Ratio Using Fibonacci Sequence at Edith Erdman blog

How Will We Determine Golden Ratio Using Fibonacci Sequence. The new ratio is (a + b)/a (a + b) / a. When you divide the larger one by the smaller one, the answer is something close to phi. Understand why fibonacci numbers, the golden ratio and the golden spiral appear in nature, and why we find them so pleasing to look at. The notation that we will use to represent the fibonacci sequence is as follows: The further you go along the fibonacci sequence, the closer the answers get to phi. Another ratio is found by adding the two numbers together a + b a + b and dividing this by the larger number a a. We conclude the week by deriving the celebrated binet’s formula, an explicit formula for. Jun 7, 2021 • 2 min read. How to calculate the golden ratio. \[f_{1}=1, f_{2}=1, f_{3}=2, f_{4}=3, f_{5}=5, f_{6}=8,. We’re looking at the fibonacci sequence, and have seen connections to a number called phi (φ or ), commonly called the golden. With one number a a and another smaller number b b, the ratio of the two numbers is found by dividing them. The golden ratio is a famous mathematical. But the answer will never equal phi exactly. Their ratio is a/b a / b.

But the answer will never equal phi exactly. When you divide the larger one by the smaller one, the answer is something close to phi. Understand why fibonacci numbers, the golden ratio and the golden spiral appear in nature, and why we find them so pleasing to look at. Another ratio is found by adding the two numbers together a + b a + b and dividing this by the larger number a a. With one number a a and another smaller number b b, the ratio of the two numbers is found by dividing them. The golden ratio is a famous mathematical. The new ratio is (a + b)/a (a + b) / a. \[f_{1}=1, f_{2}=1, f_{3}=2, f_{4}=3, f_{5}=5, f_{6}=8,. The notation that we will use to represent the fibonacci sequence is as follows: How to calculate the golden ratio.

Generalized Fibonacci Sequence and the Golden Ratio Wolfram

How Will We Determine Golden Ratio Using Fibonacci Sequence We’re looking at the fibonacci sequence, and have seen connections to a number called phi (φ or ), commonly called the golden. The golden ratio is a relationship between two numbers that are next to each other in the fibonacci sequence. When you divide the larger one by the smaller one, the answer is something close to phi. But the answer will never equal phi exactly. \[f_{1}=1, f_{2}=1, f_{3}=2, f_{4}=3, f_{5}=5, f_{6}=8,. The notation that we will use to represent the fibonacci sequence is as follows: Understand why fibonacci numbers, the golden ratio and the golden spiral appear in nature, and why we find them so pleasing to look at. With one number a a and another smaller number b b, the ratio of the two numbers is found by dividing them. The new ratio is (a + b)/a (a + b) / a. We’re looking at the fibonacci sequence, and have seen connections to a number called phi (φ or ), commonly called the golden. The further you go along the fibonacci sequence, the closer the answers get to phi. The golden ratio is a famous mathematical. We conclude the week by deriving the celebrated binet’s formula, an explicit formula for. Jun 7, 2021 • 2 min read. How to calculate the golden ratio. Another ratio is found by adding the two numbers together a + b a + b and dividing this by the larger number a a.