Standard Basis For C2 . (a complex vector space is a complexification if. After reading the following post (what is the standard basis for fields of complex numbers?), i tried to confirm that the suggested. , 0) (1 in the ith place). , en), ei = (0,. I know the standard for $\bbb r^2$ is $((1, 0), (0,. It depends on the scalar field f because the dimension could change thereby changing the number of elements in. $(a + bi, c + di)$)? I'm looking for a listing of the canonical basis for the most common vector spaces. One advantage of the standard basis is that it’s easy to write. Some standard basis are not so obvious. The complex vector subspace ⊂ c2 spanned by ( ) provides a. A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single.
from www.chegg.com
Some standard basis are not so obvious. , 0) (1 in the ith place). A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. It depends on the scalar field f because the dimension could change thereby changing the number of elements in. , en), ei = (0,. $(a + bi, c + di)$)? I know the standard for $\bbb r^2$ is $((1, 0), (0,. The complex vector subspace ⊂ c2 spanned by ( ) provides a. (a complex vector space is a complexification if. I'm looking for a listing of the canonical basis for the most common vector spaces.
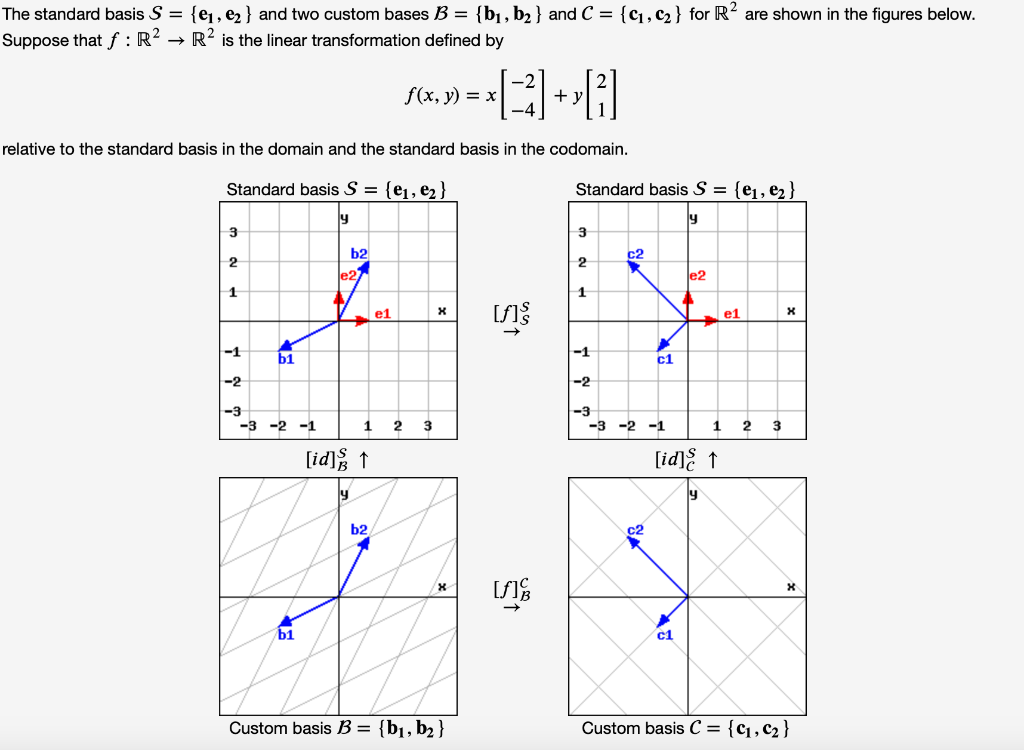
Solved The standard basis S={e1,e2} and two custom bases
Standard Basis For C2 I'm looking for a listing of the canonical basis for the most common vector spaces. , 0) (1 in the ith place). One advantage of the standard basis is that it’s easy to write. I'm looking for a listing of the canonical basis for the most common vector spaces. (a complex vector space is a complexification if. $(a + bi, c + di)$)? After reading the following post (what is the standard basis for fields of complex numbers?), i tried to confirm that the suggested. Some standard basis are not so obvious. , en), ei = (0,. A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. I know the standard for $\bbb r^2$ is $((1, 0), (0,. The complex vector subspace ⊂ c2 spanned by ( ) provides a. It depends on the scalar field f because the dimension could change thereby changing the number of elements in.
From www.chegg.com
Solved The standard basis ={e1,e2} and two custom bases Standard Basis For C2 A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. It depends on the scalar field f because the dimension could change thereby changing the number of elements in. , 0) (1 in the ith place). The complex vector subspace ⊂ c2 spanned by ( ) provides a.. Standard Basis For C2.
From www.chegg.com
Solved The standard basis S={e1,e2} and two custom bases Standard Basis For C2 , en), ei = (0,. I know the standard for $\bbb r^2$ is $((1, 0), (0,. I'm looking for a listing of the canonical basis for the most common vector spaces. The complex vector subspace ⊂ c2 spanned by ( ) provides a. Some standard basis are not so obvious. A standard basis, also called a natural basis, is a. Standard Basis For C2.
From www.youtube.com
Use the Standard Basis to Find a Standard Matrix YouTube Standard Basis For C2 One advantage of the standard basis is that it’s easy to write. , 0) (1 in the ith place). , en), ei = (0,. After reading the following post (what is the standard basis for fields of complex numbers?), i tried to confirm that the suggested. (a complex vector space is a complexification if. $(a + bi, c + di)$)?. Standard Basis For C2.
From www.chegg.com
Solved he standard basis S={e1,e2} and two custom bases Standard Basis For C2 I'm looking for a listing of the canonical basis for the most common vector spaces. $(a + bi, c + di)$)? (a complex vector space is a complexification if. A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. , 0) (1 in the ith place). After reading. Standard Basis For C2.
From www.chegg.com
Solved The standard basis S={e1,c2} and a custom basis Standard Basis For C2 It depends on the scalar field f because the dimension could change thereby changing the number of elements in. After reading the following post (what is the standard basis for fields of complex numbers?), i tried to confirm that the suggested. The complex vector subspace ⊂ c2 spanned by ( ) provides a. , en), ei = (0,. , 0). Standard Basis For C2.
From www.academia.edu
(PDF) XML standards as the basis for data interoperability among Standard Basis For C2 Some standard basis are not so obvious. I know the standard for $\bbb r^2$ is $((1, 0), (0,. One advantage of the standard basis is that it’s easy to write. (a complex vector space is a complexification if. , en), ei = (0,. It depends on the scalar field f because the dimension could change thereby changing the number of. Standard Basis For C2.
From www.youtube.com
MOT Theory of C2 Molecule Bonding in C2 Molecule Bond order of C2 Standard Basis For C2 After reading the following post (what is the standard basis for fields of complex numbers?), i tried to confirm that the suggested. It depends on the scalar field f because the dimension could change thereby changing the number of elements in. I'm looking for a listing of the canonical basis for the most common vector spaces. I know the standard. Standard Basis For C2.
From www.chegg.com
Solved (1 point) The standard basis E = {e1,e2 } and two Standard Basis For C2 $(a + bi, c + di)$)? , en), ei = (0,. A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. After reading the following post (what is the standard basis for fields of complex numbers?), i tried to confirm that the suggested. It depends on the scalar. Standard Basis For C2.
From www.chegg.com
Solved (1 point) The standard basis S = {eu, ez) and two Standard Basis For C2 , en), ei = (0,. , 0) (1 in the ith place). $(a + bi, c + di)$)? Some standard basis are not so obvious. I'm looking for a listing of the canonical basis for the most common vector spaces. It depends on the scalar field f because the dimension could change thereby changing the number of elements in. The. Standard Basis For C2.
From www.chegg.com
The standard basis S = (ei, e2} and two custom bases Standard Basis For C2 Some standard basis are not so obvious. It depends on the scalar field f because the dimension could change thereby changing the number of elements in. A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. I know the standard for $\bbb r^2$ is $((1, 0), (0,. One. Standard Basis For C2.
From www.slideserve.com
PPT Finding Eigenvalues and Eigenvectors PowerPoint Presentation Standard Basis For C2 I know the standard for $\bbb r^2$ is $((1, 0), (0,. I'm looking for a listing of the canonical basis for the most common vector spaces. It depends on the scalar field f because the dimension could change thereby changing the number of elements in. One advantage of the standard basis is that it’s easy to write. After reading the. Standard Basis For C2.
From www.slideserve.com
PPT Vectors PowerPoint Presentation, free download ID568692 Standard Basis For C2 (a complex vector space is a complexification if. A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. One advantage of the standard basis is that it’s easy to write. The complex vector subspace ⊂ c2 spanned by ( ) provides a. Some standard basis are not so. Standard Basis For C2.
From www.youtube.com
Finding a Standard Matrix Using the Standard Basis YouTube Standard Basis For C2 I'm looking for a listing of the canonical basis for the most common vector spaces. I know the standard for $\bbb r^2$ is $((1, 0), (0,. , en), ei = (0,. It depends on the scalar field f because the dimension could change thereby changing the number of elements in. A standard basis, also called a natural basis, is a. Standard Basis For C2.
From www.chegg.com
Solved The standard basis S={e1,e2} and two custom bases Standard Basis For C2 It depends on the scalar field f because the dimension could change thereby changing the number of elements in. (a complex vector space is a complexification if. Some standard basis are not so obvious. , 0) (1 in the ith place). The complex vector subspace ⊂ c2 spanned by ( ) provides a. I know the standard for $\bbb r^2$. Standard Basis For C2.
From www.slideserve.com
PPT 5.4 Basis And Dimension PowerPoint Presentation, free download Standard Basis For C2 , 0) (1 in the ith place). , en), ei = (0,. I'm looking for a listing of the canonical basis for the most common vector spaces. After reading the following post (what is the standard basis for fields of complex numbers?), i tried to confirm that the suggested. $(a + bi, c + di)$)? Some standard basis are not. Standard Basis For C2.
From www.coursehero.com
[Solved] . Find the coordinate matrix of X relative to the standard Standard Basis For C2 One advantage of the standard basis is that it’s easy to write. , en), ei = (0,. After reading the following post (what is the standard basis for fields of complex numbers?), i tried to confirm that the suggested. (a complex vector space is a complexification if. A standard basis, also called a natural basis, is a special orthonormal vector. Standard Basis For C2.
From www.chegg.com
Solved The standard basis S={e1,e2} and two custom bases Standard Basis For C2 The complex vector subspace ⊂ c2 spanned by ( ) provides a. (a complex vector space is a complexification if. , 0) (1 in the ith place). Some standard basis are not so obvious. One advantage of the standard basis is that it’s easy to write. A standard basis, also called a natural basis, is a special orthonormal vector basis. Standard Basis For C2.
From www.chegg.com
Solved (1 point) The standard basis S = {21, 22 } and two Standard Basis For C2 A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. I'm looking for a listing of the canonical basis for the most common vector spaces. One advantage of the standard basis is that it’s easy to write. Some standard basis are not so obvious. , 0) (1 in. Standard Basis For C2.
From quizdbbarnstorms.z21.web.core.windows.net
What Is The Standard Basis Standard Basis For C2 One advantage of the standard basis is that it’s easy to write. (a complex vector space is a complexification if. I'm looking for a listing of the canonical basis for the most common vector spaces. , en), ei = (0,. After reading the following post (what is the standard basis for fields of complex numbers?), i tried to confirm that. Standard Basis For C2.
From www.youtube.com
Standard Basis Vectors YouTube Standard Basis For C2 It depends on the scalar field f because the dimension could change thereby changing the number of elements in. $(a + bi, c + di)$)? I'm looking for a listing of the canonical basis for the most common vector spaces. (a complex vector space is a complexification if. The complex vector subspace ⊂ c2 spanned by ( ) provides a.. Standard Basis For C2.
From www.youtube.com
What is a standard basis? YouTube Standard Basis For C2 The complex vector subspace ⊂ c2 spanned by ( ) provides a. , 0) (1 in the ith place). It depends on the scalar field f because the dimension could change thereby changing the number of elements in. I'm looking for a listing of the canonical basis for the most common vector spaces. After reading the following post (what is. Standard Basis For C2.
From www.numerade.com
SOLVED The standard basis = {e1, e2} and two custom bases B = {b1, bz Standard Basis For C2 I'm looking for a listing of the canonical basis for the most common vector spaces. $(a + bi, c + di)$)? The complex vector subspace ⊂ c2 spanned by ( ) provides a. After reading the following post (what is the standard basis for fields of complex numbers?), i tried to confirm that the suggested. One advantage of the standard. Standard Basis For C2.
From www.chegg.com
Solved The standard basis S={e1,e2} and two custom bases Standard Basis For C2 One advantage of the standard basis is that it’s easy to write. After reading the following post (what is the standard basis for fields of complex numbers?), i tried to confirm that the suggested. It depends on the scalar field f because the dimension could change thereby changing the number of elements in. A standard basis, also called a natural. Standard Basis For C2.
From www.youtube.com
The Standard Basis of a General Linear Transformation YouTube Standard Basis For C2 Some standard basis are not so obvious. I'm looking for a listing of the canonical basis for the most common vector spaces. I know the standard for $\bbb r^2$ is $((1, 0), (0,. (a complex vector space is a complexification if. $(a + bi, c + di)$)? A standard basis, also called a natural basis, is a special orthonormal vector. Standard Basis For C2.
From www.chegg.com
Solved 9 Let (a1, A2, A3, A4) be a standard basis of R4, and Standard Basis For C2 , 0) (1 in the ith place). One advantage of the standard basis is that it’s easy to write. Some standard basis are not so obvious. It depends on the scalar field f because the dimension could change thereby changing the number of elements in. The complex vector subspace ⊂ c2 spanned by ( ) provides a. After reading the. Standard Basis For C2.
From www.chegg.com
Solved The standard basis S={e1,e2} and two custom bases Standard Basis For C2 After reading the following post (what is the standard basis for fields of complex numbers?), i tried to confirm that the suggested. , 0) (1 in the ith place). Some standard basis are not so obvious. I'm looking for a listing of the canonical basis for the most common vector spaces. (a complex vector space is a complexification if. ,. Standard Basis For C2.
From www.chegg.com
Solved Find the change of basis matrix from the standard Standard Basis For C2 A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. One advantage of the standard basis is that it’s easy to write. , 0) (1 in the ith place). It depends on the scalar field f because the dimension could change thereby changing the number of elements in.. Standard Basis For C2.
From www.chegg.com
Solved The standard basis S={e1,c2} and two custom bases Standard Basis For C2 (a complex vector space is a complexification if. After reading the following post (what is the standard basis for fields of complex numbers?), i tried to confirm that the suggested. I know the standard for $\bbb r^2$ is $((1, 0), (0,. It depends on the scalar field f because the dimension could change thereby changing the number of elements in.. Standard Basis For C2.
From www.chegg.com
Solved (1 point) The set is called the standard basis of the Standard Basis For C2 Some standard basis are not so obvious. I know the standard for $\bbb r^2$ is $((1, 0), (0,. , 0) (1 in the ith place). It depends on the scalar field f because the dimension could change thereby changing the number of elements in. (a complex vector space is a complexification if. One advantage of the standard basis is that. Standard Basis For C2.
From www.chegg.com
Solved (1 point) The standard basis S {1,2} and two custom Standard Basis For C2 I know the standard for $\bbb r^2$ is $((1, 0), (0,. Some standard basis are not so obvious. The complex vector subspace ⊂ c2 spanned by ( ) provides a. One advantage of the standard basis is that it’s easy to write. After reading the following post (what is the standard basis for fields of complex numbers?), i tried to. Standard Basis For C2.
From www.numerade.com
SOLVED Let c1, C2, C3, C4, e5, C be the standard basis in R6. Find the Standard Basis For C2 , 0) (1 in the ith place). Some standard basis are not so obvious. The complex vector subspace ⊂ c2 spanned by ( ) provides a. I know the standard for $\bbb r^2$ is $((1, 0), (0,. I'm looking for a listing of the canonical basis for the most common vector spaces. It depends on the scalar field f because. Standard Basis For C2.
From www.studyxapp.com
1 point the standard basis s 01 ez and two custom bases b b b2 and c ci Standard Basis For C2 , 0) (1 in the ith place). The complex vector subspace ⊂ c2 spanned by ( ) provides a. It depends on the scalar field f because the dimension could change thereby changing the number of elements in. Some standard basis are not so obvious. I'm looking for a listing of the canonical basis for the most common vector spaces.. Standard Basis For C2.
From www.bartleby.com
Answered The standard basis S = {e1, ez} and two… bartleby Standard Basis For C2 A standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a single. (a complex vector space is a complexification if. It depends on the scalar field f because the dimension could change thereby changing the number of elements in. , en), ei = (0,. I know the standard for $\bbb. Standard Basis For C2.
From www.chegg.com
Solved The standard basis S={e1,e2} and two custom bases Standard Basis For C2 Some standard basis are not so obvious. After reading the following post (what is the standard basis for fields of complex numbers?), i tried to confirm that the suggested. $(a + bi, c + di)$)? The complex vector subspace ⊂ c2 spanned by ( ) provides a. A standard basis, also called a natural basis, is a special orthonormal vector. Standard Basis For C2.
From www.chegg.com
Solved U (1) (30 Pts) Let V = R4 with standard basis S = Standard Basis For C2 , en), ei = (0,. One advantage of the standard basis is that it’s easy to write. I know the standard for $\bbb r^2$ is $((1, 0), (0,. , 0) (1 in the ith place). I'm looking for a listing of the canonical basis for the most common vector spaces. The complex vector subspace ⊂ c2 spanned by ( ). Standard Basis For C2.