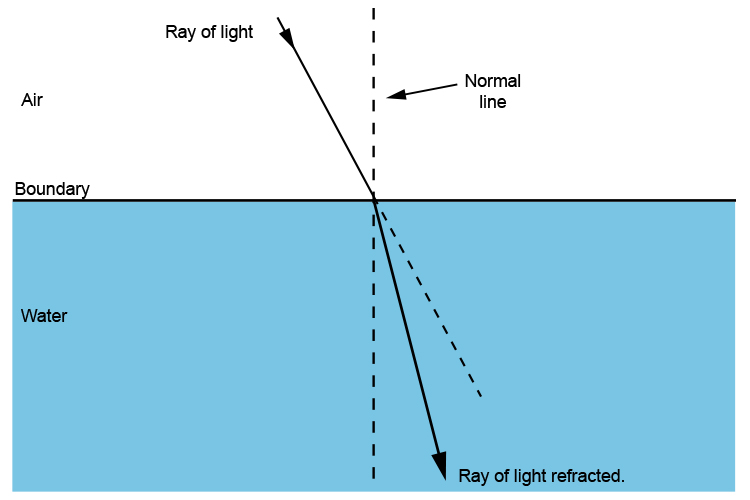
What Are Normal Lines at Emily Deaton blog

What Are Normal Lines. Because the slopes of perpendicular. The normal line is defined as the line that is perpendicular to the tangent line at the point of tangency. The normal line is the line which is perpendicular to the tangent line at the point where the tangent line intersects the function. It is called the normal line to \(s\) at \((x_0,y_0,z_0)\text{.}\) for example, the following figure shows the side view of the tangent plane (in black) and. In geometry, the normal line is perpendicular to a given line, plane, or surface at a specific point. However, there is another important type of line we need to consider called a normal. So far, we have been focused on tangent lines. When dealing with a function \(y=f(x)\) of one variable, we stated that a line through \((c,f(c))\) was tangent to \(f\) if. In the context of surfaces, we have the gradient vector of the surface at a given. Definition of the normal line. Given a vector and a point, there is a unique line parallel to that vector that passes through the point.

It is called the normal line to \(s\) at \((x_0,y_0,z_0)\text{.}\) for example, the following figure shows the side view of the tangent plane (in black) and. In the context of surfaces, we have the gradient vector of the surface at a given. Definition of the normal line. Given a vector and a point, there is a unique line parallel to that vector that passes through the point. When dealing with a function \(y=f(x)\) of one variable, we stated that a line through \((c,f(c))\) was tangent to \(f\) if. The normal line is the line which is perpendicular to the tangent line at the point where the tangent line intersects the function. However, there is another important type of line we need to consider called a normal. So far, we have been focused on tangent lines. Because the slopes of perpendicular. The normal line is defined as the line that is perpendicular to the tangent line at the point of tangency.

Normal line Flat surfaces

What Are Normal Lines When dealing with a function \(y=f(x)\) of one variable, we stated that a line through \((c,f(c))\) was tangent to \(f\) if. Definition of the normal line. In the context of surfaces, we have the gradient vector of the surface at a given. So far, we have been focused on tangent lines. Given a vector and a point, there is a unique line parallel to that vector that passes through the point. However, there is another important type of line we need to consider called a normal. Because the slopes of perpendicular. In geometry, the normal line is perpendicular to a given line, plane, or surface at a specific point. When dealing with a function \(y=f(x)\) of one variable, we stated that a line through \((c,f(c))\) was tangent to \(f\) if. The normal line is the line which is perpendicular to the tangent line at the point where the tangent line intersects the function. The normal line is defined as the line that is perpendicular to the tangent line at the point of tangency. It is called the normal line to \(s\) at \((x_0,y_0,z_0)\text{.}\) for example, the following figure shows the side view of the tangent plane (in black) and.