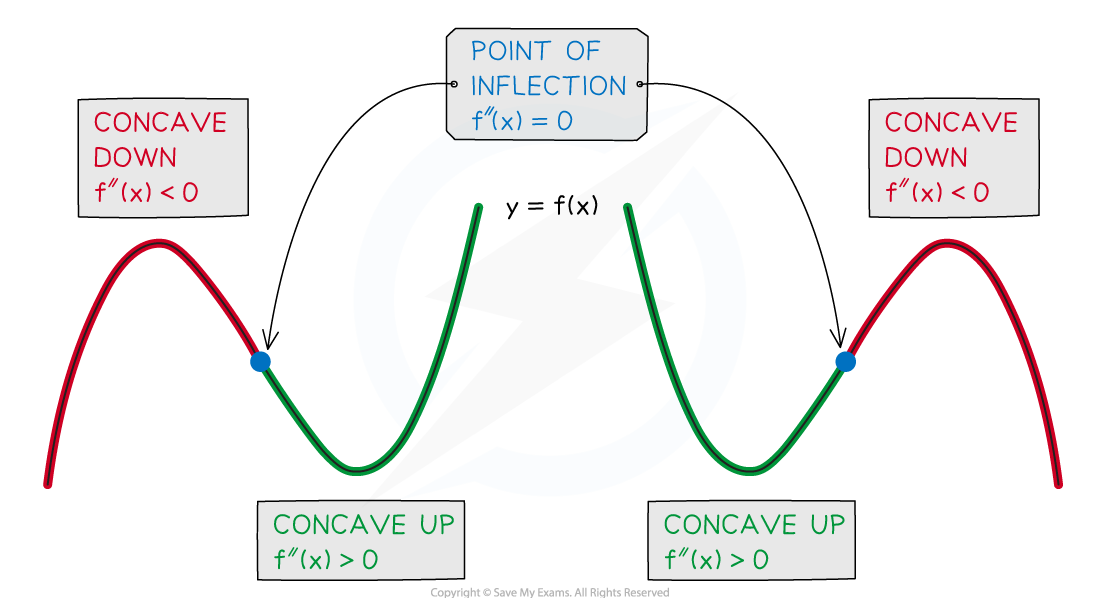
Points Of Inflection For Normal Curve . Learn how to graph and interpret normal curves, which are symmetric, unimodal, and bellshaped continuous probability distributions. If a variable has this distribution, its sd is 1. The points at which the curve changes from being concave up to being concave down are called the inflection points. It is the following known characteristics of the normal curve that directed me in drawing the curve as i did so. The probability density function of the normal distribution with mean $\mu$ and variance $\sigma^2$ has two inflection. The normal curve is one of the very few distributions. I am looking to show that $f_x(x)$ has points of inflections at $x = \mu \pm \sigma$. The density of $x$ is the normal distribution. Characteristics of a normal curve.
from www.linstitute.net
It is the following known characteristics of the normal curve that directed me in drawing the curve as i did so. The normal curve is one of the very few distributions. The points at which the curve changes from being concave up to being concave down are called the inflection points. Learn how to graph and interpret normal curves, which are symmetric, unimodal, and bellshaped continuous probability distributions. I am looking to show that $f_x(x)$ has points of inflections at $x = \mu \pm \sigma$. Characteristics of a normal curve. If a variable has this distribution, its sd is 1. The probability density function of the normal distribution with mean $\mu$ and variance $\sigma^2$ has two inflection. The density of $x$ is the normal distribution.
IB DP Maths AI HL复习笔记5.2.6 Concavity & Points of Inflection翰林国际教育
Points Of Inflection For Normal Curve Learn how to graph and interpret normal curves, which are symmetric, unimodal, and bellshaped continuous probability distributions. It is the following known characteristics of the normal curve that directed me in drawing the curve as i did so. The normal curve is one of the very few distributions. If a variable has this distribution, its sd is 1. The density of $x$ is the normal distribution. Learn how to graph and interpret normal curves, which are symmetric, unimodal, and bellshaped continuous probability distributions. The probability density function of the normal distribution with mean $\mu$ and variance $\sigma^2$ has two inflection. Characteristics of a normal curve. I am looking to show that $f_x(x)$ has points of inflections at $x = \mu \pm \sigma$. The points at which the curve changes from being concave up to being concave down are called the inflection points.
From slideplayer.com
Part A Concepts & binomial distributions Part B Normal distributions Points Of Inflection For Normal Curve If a variable has this distribution, its sd is 1. The density of $x$ is the normal distribution. The points at which the curve changes from being concave up to being concave down are called the inflection points. Characteristics of a normal curve. The normal curve is one of the very few distributions. The probability density function of the normal. Points Of Inflection For Normal Curve.
From slidetodoc.com
Normal Distributions Empirical Rule and Standard Normal Distribution Points Of Inflection For Normal Curve The density of $x$ is the normal distribution. Learn how to graph and interpret normal curves, which are symmetric, unimodal, and bellshaped continuous probability distributions. I am looking to show that $f_x(x)$ has points of inflections at $x = \mu \pm \sigma$. It is the following known characteristics of the normal curve that directed me in drawing the curve as. Points Of Inflection For Normal Curve.
From www.researchgate.net
Inflection points of curve in trimming direction Download Scientific Points Of Inflection For Normal Curve The normal curve is one of the very few distributions. The density of $x$ is the normal distribution. The points at which the curve changes from being concave up to being concave down are called the inflection points. If a variable has this distribution, its sd is 1. Learn how to graph and interpret normal curves, which are symmetric, unimodal,. Points Of Inflection For Normal Curve.
From www.numerade.com
Draw normal curve with u = 160 and = 20. Label the mean and the Points Of Inflection For Normal Curve The normal curve is one of the very few distributions. The probability density function of the normal distribution with mean $\mu$ and variance $\sigma^2$ has two inflection. The points at which the curve changes from being concave up to being concave down are called the inflection points. It is the following known characteristics of the normal curve that directed me. Points Of Inflection For Normal Curve.
From www.hanlin.com
AQA A Level Maths Pure复习笔记7.4.2 Points of Inflection翰林国际教育 Points Of Inflection For Normal Curve The points at which the curve changes from being concave up to being concave down are called the inflection points. If a variable has this distribution, its sd is 1. Learn how to graph and interpret normal curves, which are symmetric, unimodal, and bellshaped continuous probability distributions. The density of $x$ is the normal distribution. The probability density function of. Points Of Inflection For Normal Curve.
From stats.stackexchange.com
central limit theorem Why does the Normal Distribution have Points Of Inflection For Normal Curve The density of $x$ is the normal distribution. Characteristics of a normal curve. The points at which the curve changes from being concave up to being concave down are called the inflection points. The probability density function of the normal distribution with mean $\mu$ and variance $\sigma^2$ has two inflection. It is the following known characteristics of the normal curve. Points Of Inflection For Normal Curve.
From vayp-por.blogspot.com
Characteristics Of Normal Distribution Normal distribution curve Points Of Inflection For Normal Curve The probability density function of the normal distribution with mean $\mu$ and variance $\sigma^2$ has two inflection. If a variable has this distribution, its sd is 1. The normal curve is one of the very few distributions. The points at which the curve changes from being concave up to being concave down are called the inflection points. Learn how to. Points Of Inflection For Normal Curve.
From slidetodoc.com
The Normal Probability Distribution Points of Inflection s Points Of Inflection For Normal Curve If a variable has this distribution, its sd is 1. The points at which the curve changes from being concave up to being concave down are called the inflection points. It is the following known characteristics of the normal curve that directed me in drawing the curve as i did so. The probability density function of the normal distribution with. Points Of Inflection For Normal Curve.
From www.researchgate.net
Examples of different points on the PV curve that have been proposed Points Of Inflection For Normal Curve The density of $x$ is the normal distribution. Learn how to graph and interpret normal curves, which are symmetric, unimodal, and bellshaped continuous probability distributions. The probability density function of the normal distribution with mean $\mu$ and variance $\sigma^2$ has two inflection. I am looking to show that $f_x(x)$ has points of inflections at $x = \mu \pm \sigma$. The. Points Of Inflection For Normal Curve.
From www.chegg.com
Solved Draw a normal curve with u 68 and o = 15. Label the Points Of Inflection For Normal Curve The points at which the curve changes from being concave up to being concave down are called the inflection points. If a variable has this distribution, its sd is 1. Characteristics of a normal curve. The probability density function of the normal distribution with mean $\mu$ and variance $\sigma^2$ has two inflection. The normal curve is one of the very. Points Of Inflection For Normal Curve.
From studylib.net
Inflection points of the bellshaped curve Points Of Inflection For Normal Curve If a variable has this distribution, its sd is 1. The density of $x$ is the normal distribution. The points at which the curve changes from being concave up to being concave down are called the inflection points. The probability density function of the normal distribution with mean $\mu$ and variance $\sigma^2$ has two inflection. It is the following known. Points Of Inflection For Normal Curve.
From mammothmemory.net
A bell curves can be skewed negatively or positively Points Of Inflection For Normal Curve Learn how to graph and interpret normal curves, which are symmetric, unimodal, and bellshaped continuous probability distributions. The points at which the curve changes from being concave up to being concave down are called the inflection points. The density of $x$ is the normal distribution. If a variable has this distribution, its sd is 1. It is the following known. Points Of Inflection For Normal Curve.
From www.linstitute.net
IB DP Maths AI HL复习笔记5.2.6 Concavity & Points of Inflection翰林国际教育 Points Of Inflection For Normal Curve Learn how to graph and interpret normal curves, which are symmetric, unimodal, and bellshaped continuous probability distributions. The normal curve is one of the very few distributions. It is the following known characteristics of the normal curve that directed me in drawing the curve as i did so. I am looking to show that $f_x(x)$ has points of inflections at. Points Of Inflection For Normal Curve.
From www.slideserve.com
PPT A Pragmatic Introduction to the Gaussian Curve PowerPoint Points Of Inflection For Normal Curve The points at which the curve changes from being concave up to being concave down are called the inflection points. The density of $x$ is the normal distribution. Learn how to graph and interpret normal curves, which are symmetric, unimodal, and bellshaped continuous probability distributions. The normal curve is one of the very few distributions. It is the following known. Points Of Inflection For Normal Curve.
From www.radfordmathematics.com
Point of Inflection Calculus Points Of Inflection For Normal Curve The normal curve is one of the very few distributions. The density of $x$ is the normal distribution. The points at which the curve changes from being concave up to being concave down are called the inflection points. I am looking to show that $f_x(x)$ has points of inflections at $x = \mu \pm \sigma$. If a variable has this. Points Of Inflection For Normal Curve.
From phuongndc.medium.com
Inflection Point — A powerful data analytics method by PhuongNDC Medium Points Of Inflection For Normal Curve The density of $x$ is the normal distribution. The normal curve is one of the very few distributions. The probability density function of the normal distribution with mean $\mu$ and variance $\sigma^2$ has two inflection. It is the following known characteristics of the normal curve that directed me in drawing the curve as i did so. Learn how to graph. Points Of Inflection For Normal Curve.
From www.slideserve.com
PPT Chapter 2 The Normal Distributions PowerPoint Presentation, free Points Of Inflection For Normal Curve The points at which the curve changes from being concave up to being concave down are called the inflection points. The probability density function of the normal distribution with mean $\mu$ and variance $\sigma^2$ has two inflection. The density of $x$ is the normal distribution. Learn how to graph and interpret normal curves, which are symmetric, unimodal, and bellshaped continuous. Points Of Inflection For Normal Curve.
From www.numerade.com
SOLVED For the following normal distribution, give the xvalues of the Points Of Inflection For Normal Curve I am looking to show that $f_x(x)$ has points of inflections at $x = \mu \pm \sigma$. Characteristics of a normal curve. If a variable has this distribution, its sd is 1. The density of $x$ is the normal distribution. The points at which the curve changes from being concave up to being concave down are called the inflection points.. Points Of Inflection For Normal Curve.
From www.chegg.com
Solved 4. Consider the normal distribution represented by Points Of Inflection For Normal Curve The points at which the curve changes from being concave up to being concave down are called the inflection points. Characteristics of a normal curve. It is the following known characteristics of the normal curve that directed me in drawing the curve as i did so. I am looking to show that $f_x(x)$ has points of inflections at $x =. Points Of Inflection For Normal Curve.
From stats.stackexchange.com
central limit theorem Why does the Normal Distribution have Points Of Inflection For Normal Curve If a variable has this distribution, its sd is 1. It is the following known characteristics of the normal curve that directed me in drawing the curve as i did so. I am looking to show that $f_x(x)$ has points of inflections at $x = \mu \pm \sigma$. Characteristics of a normal curve. Learn how to graph and interpret normal. Points Of Inflection For Normal Curve.
From www.numerade.com
Draw a normal curve with mu =58 and sigma =15. Label the mean and the Points Of Inflection For Normal Curve Characteristics of a normal curve. Learn how to graph and interpret normal curves, which are symmetric, unimodal, and bellshaped continuous probability distributions. The density of $x$ is the normal distribution. The points at which the curve changes from being concave up to being concave down are called the inflection points. The normal curve is one of the very few distributions.. Points Of Inflection For Normal Curve.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Points Of Inflection For Normal Curve The points at which the curve changes from being concave up to being concave down are called the inflection points. Characteristics of a normal curve. The probability density function of the normal distribution with mean $\mu$ and variance $\sigma^2$ has two inflection. If a variable has this distribution, its sd is 1. The density of $x$ is the normal distribution.. Points Of Inflection For Normal Curve.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Points Of Inflection For Normal Curve Characteristics of a normal curve. The density of $x$ is the normal distribution. It is the following known characteristics of the normal curve that directed me in drawing the curve as i did so. If a variable has this distribution, its sd is 1. The points at which the curve changes from being concave up to being concave down are. Points Of Inflection For Normal Curve.
From www.nagwa.com
Question Video Finding All Inflection Points of the Curve of a Points Of Inflection For Normal Curve It is the following known characteristics of the normal curve that directed me in drawing the curve as i did so. The points at which the curve changes from being concave up to being concave down are called the inflection points. The probability density function of the normal distribution with mean $\mu$ and variance $\sigma^2$ has two inflection. If a. Points Of Inflection For Normal Curve.
From quizlet.com
Draw a normal curve and label the mean and inflection points Quizlet Points Of Inflection For Normal Curve The points at which the curve changes from being concave up to being concave down are called the inflection points. The probability density function of the normal distribution with mean $\mu$ and variance $\sigma^2$ has two inflection. The normal curve is one of the very few distributions. I am looking to show that $f_x(x)$ has points of inflections at $x. Points Of Inflection For Normal Curve.
From www.slideserve.com
PPT Chapter 2 The Normal Distributions PowerPoint Presentation, free Points Of Inflection For Normal Curve Characteristics of a normal curve. If a variable has this distribution, its sd is 1. I am looking to show that $f_x(x)$ has points of inflections at $x = \mu \pm \sigma$. It is the following known characteristics of the normal curve that directed me in drawing the curve as i did so. The points at which the curve changes. Points Of Inflection For Normal Curve.
From stats.stackexchange.com
central limit theorem Why does the Normal Distribution have Points Of Inflection For Normal Curve The density of $x$ is the normal distribution. Characteristics of a normal curve. The normal curve is one of the very few distributions. It is the following known characteristics of the normal curve that directed me in drawing the curve as i did so. The probability density function of the normal distribution with mean $\mu$ and variance $\sigma^2$ has two. Points Of Inflection For Normal Curve.
From www.slideshare.net
Normal Probability Distribution Points Of Inflection For Normal Curve If a variable has this distribution, its sd is 1. The probability density function of the normal distribution with mean $\mu$ and variance $\sigma^2$ has two inflection. The normal curve is one of the very few distributions. Characteristics of a normal curve. It is the following known characteristics of the normal curve that directed me in drawing the curve as. Points Of Inflection For Normal Curve.
From www.varsitytutors.com
Fitting Data Sets to Normal Distribution and Estimating Area Under the Points Of Inflection For Normal Curve If a variable has this distribution, its sd is 1. I am looking to show that $f_x(x)$ has points of inflections at $x = \mu \pm \sigma$. Learn how to graph and interpret normal curves, which are symmetric, unimodal, and bellshaped continuous probability distributions. It is the following known characteristics of the normal curve that directed me in drawing the. Points Of Inflection For Normal Curve.
From www.numerade.com
SOLVED Describe the inflection points on the graph of a normal Points Of Inflection For Normal Curve The points at which the curve changes from being concave up to being concave down are called the inflection points. The normal curve is one of the very few distributions. The probability density function of the normal distribution with mean $\mu$ and variance $\sigma^2$ has two inflection. If a variable has this distribution, its sd is 1. It is the. Points Of Inflection For Normal Curve.
From www.slideserve.com
PPT Chapter 5 The Normal Distribution PowerPoint Presentation, free Points Of Inflection For Normal Curve The normal curve is one of the very few distributions. The probability density function of the normal distribution with mean $\mu$ and variance $\sigma^2$ has two inflection. Characteristics of a normal curve. The points at which the curve changes from being concave up to being concave down are called the inflection points. The density of $x$ is the normal distribution.. Points Of Inflection For Normal Curve.
From 28left.github.io
Inflection Points — Penn State Math 110 Companion Site Points Of Inflection For Normal Curve It is the following known characteristics of the normal curve that directed me in drawing the curve as i did so. The normal curve is one of the very few distributions. If a variable has this distribution, its sd is 1. Learn how to graph and interpret normal curves, which are symmetric, unimodal, and bellshaped continuous probability distributions. The points. Points Of Inflection For Normal Curve.
From www.chegg.com
Solved Draw a normal curve with u 58 and o =17. Label the Points Of Inflection For Normal Curve The probability density function of the normal distribution with mean $\mu$ and variance $\sigma^2$ has two inflection. The points at which the curve changes from being concave up to being concave down are called the inflection points. The normal curve is one of the very few distributions. I am looking to show that $f_x(x)$ has points of inflections at $x. Points Of Inflection For Normal Curve.
From quizlet.com
Draw a normal curve and label the mean and inflection points Quizlet Points Of Inflection For Normal Curve The density of $x$ is the normal distribution. If a variable has this distribution, its sd is 1. The normal curve is one of the very few distributions. I am looking to show that $f_x(x)$ has points of inflections at $x = \mu \pm \sigma$. Learn how to graph and interpret normal curves, which are symmetric, unimodal, and bellshaped continuous. Points Of Inflection For Normal Curve.
From bookdown.org
Chapter 5 Probability Distributions Advanced Statistics I & II Points Of Inflection For Normal Curve I am looking to show that $f_x(x)$ has points of inflections at $x = \mu \pm \sigma$. The normal curve is one of the very few distributions. The points at which the curve changes from being concave up to being concave down are called the inflection points. Characteristics of a normal curve. Learn how to graph and interpret normal curves,. Points Of Inflection For Normal Curve.