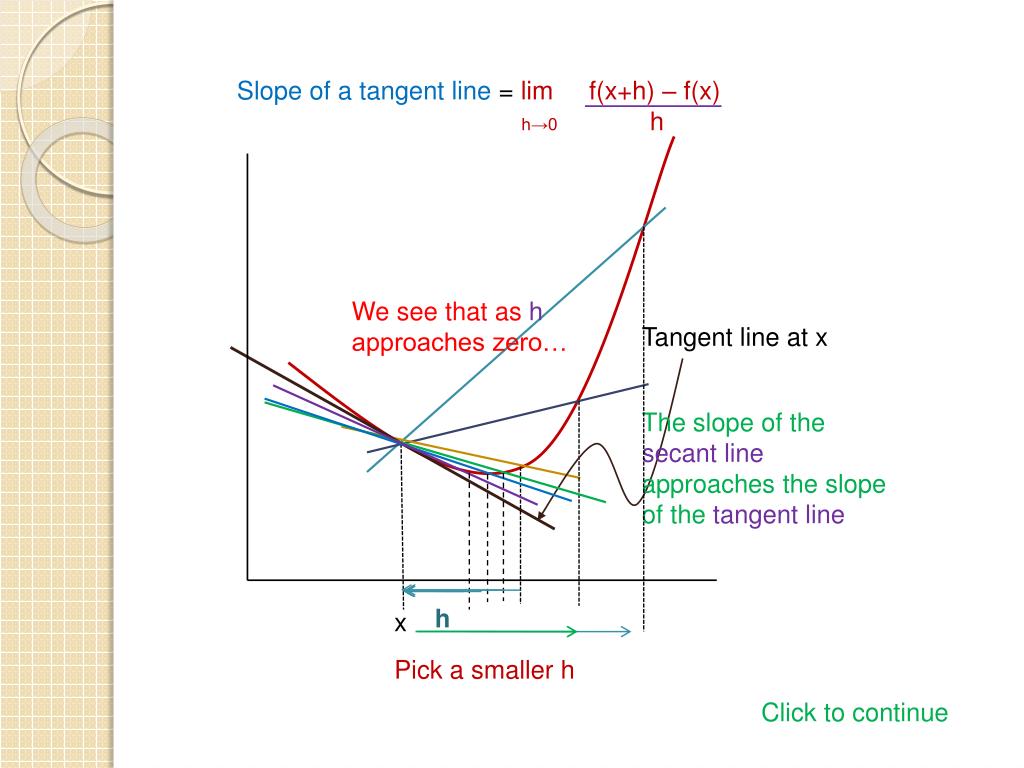
Tangent Line Gradient Zero . Given a differentiable function f and a point (x 0, y 0) the equation for the tangent line to the function f at (x 0,. Y2), the slope of the line through these two. — when dealing with a function \(y=f(x)\) of one variable, we stated that a line through \((c,f(c))\) was tangent to \(f\). the gradient theorem is useful for example because it allows to get tangent planes and tangent lines very fast, faster than by. The slope of a vertical tangent line is. tangent lines are a fundamental concept in calculus that help us understand how a curve behaves at a single point. By finding the slope of the. — in this section discuss how the gradient vector can be used to find tangent planes to a much more general.
from www.slideserve.com
— in this section discuss how the gradient vector can be used to find tangent planes to a much more general. tangent lines are a fundamental concept in calculus that help us understand how a curve behaves at a single point. The slope of a vertical tangent line is. — when dealing with a function \(y=f(x)\) of one variable, we stated that a line through \((c,f(c))\) was tangent to \(f\). the gradient theorem is useful for example because it allows to get tangent planes and tangent lines very fast, faster than by. Given a differentiable function f and a point (x 0, y 0) the equation for the tangent line to the function f at (x 0,. Y2), the slope of the line through these two. By finding the slope of the.
PPT Tangent Line using a limit PowerPoint Presentation, free download
Tangent Line Gradient Zero By finding the slope of the. Given a differentiable function f and a point (x 0, y 0) the equation for the tangent line to the function f at (x 0,. the gradient theorem is useful for example because it allows to get tangent planes and tangent lines very fast, faster than by. — when dealing with a function \(y=f(x)\) of one variable, we stated that a line through \((c,f(c))\) was tangent to \(f\). The slope of a vertical tangent line is. Y2), the slope of the line through these two. tangent lines are a fundamental concept in calculus that help us understand how a curve behaves at a single point. By finding the slope of the. — in this section discuss how the gradient vector can be used to find tangent planes to a much more general.
From www.slideserve.com
PPT Tangent Line using a limit PowerPoint Presentation, free download Tangent Line Gradient Zero — in this section discuss how the gradient vector can be used to find tangent planes to a much more general. — when dealing with a function \(y=f(x)\) of one variable, we stated that a line through \((c,f(c))\) was tangent to \(f\). The slope of a vertical tangent line is. tangent lines are a fundamental concept in. Tangent Line Gradient Zero.
From www.youtube.com
gradient of a tangent YouTube Tangent Line Gradient Zero — in this section discuss how the gradient vector can be used to find tangent planes to a much more general. the gradient theorem is useful for example because it allows to get tangent planes and tangent lines very fast, faster than by. By finding the slope of the. tangent lines are a fundamental concept in calculus. Tangent Line Gradient Zero.
From www.slideserve.com
PPT Gradient of a Curve this is given by the gradient of the tangent Tangent Line Gradient Zero Given a differentiable function f and a point (x 0, y 0) the equation for the tangent line to the function f at (x 0,. — in this section discuss how the gradient vector can be used to find tangent planes to a much more general. the gradient theorem is useful for example because it allows to get. Tangent Line Gradient Zero.
From www.slideserve.com
PPT The Derivative and the Tangent Line Problem PowerPoint Tangent Line Gradient Zero — in this section discuss how the gradient vector can be used to find tangent planes to a much more general. the gradient theorem is useful for example because it allows to get tangent planes and tangent lines very fast, faster than by. By finding the slope of the. Given a differentiable function f and a point (x. Tangent Line Gradient Zero.
From quizlet.com
Use the graph to estimate the slope of the tangent line to Quizlet Tangent Line Gradient Zero the gradient theorem is useful for example because it allows to get tangent planes and tangent lines very fast, faster than by. The slope of a vertical tangent line is. — when dealing with a function \(y=f(x)\) of one variable, we stated that a line through \((c,f(c))\) was tangent to \(f\). — in this section discuss how. Tangent Line Gradient Zero.
From owlcation.com
Math How to Find the Tangent Line of a Function in a Point Owlcation Tangent Line Gradient Zero Given a differentiable function f and a point (x 0, y 0) the equation for the tangent line to the function f at (x 0,. The slope of a vertical tangent line is. the gradient theorem is useful for example because it allows to get tangent planes and tangent lines very fast, faster than by. — in this. Tangent Line Gradient Zero.
From www.youtube.com
Ex Approximate the Slope of a Tangent Line at at a Point on a Function Tangent Line Gradient Zero Y2), the slope of the line through these two. By finding the slope of the. — when dealing with a function \(y=f(x)\) of one variable, we stated that a line through \((c,f(c))\) was tangent to \(f\). the gradient theorem is useful for example because it allows to get tangent planes and tangent lines very fast, faster than by.. Tangent Line Gradient Zero.
From thirdspacelearning.com
Equation Of Tangent GCSE Maths Steps, Examples, Worksheet Tangent Line Gradient Zero tangent lines are a fundamental concept in calculus that help us understand how a curve behaves at a single point. Y2), the slope of the line through these two. — when dealing with a function \(y=f(x)\) of one variable, we stated that a line through \((c,f(c))\) was tangent to \(f\). By finding the slope of the. The slope. Tangent Line Gradient Zero.
From www.slideserve.com
PPT Equation of Tangent line PowerPoint Presentation, free download Tangent Line Gradient Zero the gradient theorem is useful for example because it allows to get tangent planes and tangent lines very fast, faster than by. The slope of a vertical tangent line is. tangent lines are a fundamental concept in calculus that help us understand how a curve behaves at a single point. Y2), the slope of the line through these. Tangent Line Gradient Zero.
From www.storyofmathematics.com
Tangent Line Definition & Meaning Tangent Line Gradient Zero the gradient theorem is useful for example because it allows to get tangent planes and tangent lines very fast, faster than by. — in this section discuss how the gradient vector can be used to find tangent planes to a much more general. Given a differentiable function f and a point (x 0, y 0) the equation for. Tangent Line Gradient Zero.
From www.geogebra.org
Gradient of Tangent to Sketch the Derivative GeoGebra Tangent Line Gradient Zero By finding the slope of the. the gradient theorem is useful for example because it allows to get tangent planes and tangent lines very fast, faster than by. The slope of a vertical tangent line is. — in this section discuss how the gradient vector can be used to find tangent planes to a much more general. Y2),. Tangent Line Gradient Zero.
From www.youtube.com
The gradient of the tangent YouTube Tangent Line Gradient Zero Y2), the slope of the line through these two. — in this section discuss how the gradient vector can be used to find tangent planes to a much more general. — when dealing with a function \(y=f(x)\) of one variable, we stated that a line through \((c,f(c))\) was tangent to \(f\). The slope of a vertical tangent line. Tangent Line Gradient Zero.
From learninglab.rmit.edu.au
D2 Gradients, tangents and derivatives Learning Lab Tangent Line Gradient Zero Given a differentiable function f and a point (x 0, y 0) the equation for the tangent line to the function f at (x 0,. tangent lines are a fundamental concept in calculus that help us understand how a curve behaves at a single point. the gradient theorem is useful for example because it allows to get tangent. Tangent Line Gradient Zero.
From www.chegg.com
Solved a. Graph the function f(x) = x² 6x + 5. b. Identify Tangent Line Gradient Zero The slope of a vertical tangent line is. Given a differentiable function f and a point (x 0, y 0) the equation for the tangent line to the function f at (x 0,. Y2), the slope of the line through these two. tangent lines are a fundamental concept in calculus that help us understand how a curve behaves at. Tangent Line Gradient Zero.
From www.radfordmathematics.com
Tangents & Normals Calculus Tangent Line Gradient Zero By finding the slope of the. — in this section discuss how the gradient vector can be used to find tangent planes to a much more general. Given a differentiable function f and a point (x 0, y 0) the equation for the tangent line to the function f at (x 0,. — when dealing with a function. Tangent Line Gradient Zero.
From www.teachoo.com
Example 8 Find curve (2 ,3), slope of tangent is 2x/y2 Tangent Line Gradient Zero tangent lines are a fundamental concept in calculus that help us understand how a curve behaves at a single point. By finding the slope of the. The slope of a vertical tangent line is. — when dealing with a function \(y=f(x)\) of one variable, we stated that a line through \((c,f(c))\) was tangent to \(f\). Y2), the slope. Tangent Line Gradient Zero.
From studylib.net
Tangents and Gradients Tangent Line Gradient Zero Given a differentiable function f and a point (x 0, y 0) the equation for the tangent line to the function f at (x 0,. The slope of a vertical tangent line is. Y2), the slope of the line through these two. tangent lines are a fundamental concept in calculus that help us understand how a curve behaves at. Tangent Line Gradient Zero.
From www.slideserve.com
PPT Equation of Tangent line PowerPoint Presentation, free download Tangent Line Gradient Zero — in this section discuss how the gradient vector can be used to find tangent planes to a much more general. By finding the slope of the. tangent lines are a fundamental concept in calculus that help us understand how a curve behaves at a single point. The slope of a vertical tangent line is. — when. Tangent Line Gradient Zero.
From www.youtube.com
Find the Equation of The Tangent Line YouTube Tangent Line Gradient Zero Y2), the slope of the line through these two. Given a differentiable function f and a point (x 0, y 0) the equation for the tangent line to the function f at (x 0,. By finding the slope of the. tangent lines are a fundamental concept in calculus that help us understand how a curve behaves at a single. Tangent Line Gradient Zero.
From www.numerade.com
SOLVED On a contour plot of f (x,y) the directional derivative is zero Tangent Line Gradient Zero tangent lines are a fundamental concept in calculus that help us understand how a curve behaves at a single point. — in this section discuss how the gradient vector can be used to find tangent planes to a much more general. — when dealing with a function \(y=f(x)\) of one variable, we stated that a line through. Tangent Line Gradient Zero.
From www.numerade.com
SOLVEDTangent lines with zero slope a. Graph the function f(x)=x^24 Tangent Line Gradient Zero Y2), the slope of the line through these two. By finding the slope of the. tangent lines are a fundamental concept in calculus that help us understand how a curve behaves at a single point. Given a differentiable function f and a point (x 0, y 0) the equation for the tangent line to the function f at (x. Tangent Line Gradient Zero.
From www.youtube.com
Tangent line via Gradient Vector YouTube Tangent Line Gradient Zero the gradient theorem is useful for example because it allows to get tangent planes and tangent lines very fast, faster than by. Y2), the slope of the line through these two. — in this section discuss how the gradient vector can be used to find tangent planes to a much more general. tangent lines are a fundamental. Tangent Line Gradient Zero.
From www.geogebra.org
Secant and Tangent Lines on Parabola 2 GeoGebra Tangent Line Gradient Zero By finding the slope of the. — when dealing with a function \(y=f(x)\) of one variable, we stated that a line through \((c,f(c))\) was tangent to \(f\). Y2), the slope of the line through these two. the gradient theorem is useful for example because it allows to get tangent planes and tangent lines very fast, faster than by.. Tangent Line Gradient Zero.
From mungfali.com
Equation Of Tangent Line To Curve Tangent Line Gradient Zero By finding the slope of the. tangent lines are a fundamental concept in calculus that help us understand how a curve behaves at a single point. Y2), the slope of the line through these two. — in this section discuss how the gradient vector can be used to find tangent planes to a much more general. Given a. Tangent Line Gradient Zero.
From www.numerade.com
SOLVEDFind all values of x( if any ) where the tangent line to the Tangent Line Gradient Zero The slope of a vertical tangent line is. Y2), the slope of the line through these two. By finding the slope of the. — when dealing with a function \(y=f(x)\) of one variable, we stated that a line through \((c,f(c))\) was tangent to \(f\). the gradient theorem is useful for example because it allows to get tangent planes. Tangent Line Gradient Zero.
From www.cuemath.com
Tangent Definition Equation and Calculator Cuemath Tangent Line Gradient Zero — when dealing with a function \(y=f(x)\) of one variable, we stated that a line through \((c,f(c))\) was tangent to \(f\). Given a differentiable function f and a point (x 0, y 0) the equation for the tangent line to the function f at (x 0,. the gradient theorem is useful for example because it allows to get. Tangent Line Gradient Zero.
From www.wikihow.com
How to Find the Equation of a Tangent Line 8 Steps Tangent Line Gradient Zero Y2), the slope of the line through these two. — in this section discuss how the gradient vector can be used to find tangent planes to a much more general. Given a differentiable function f and a point (x 0, y 0) the equation for the tangent line to the function f at (x 0,. By finding the slope. Tangent Line Gradient Zero.
From www.cuemath.com
Tangent Line Equation, Slope, Horizontal Point of Tangency Tangent Line Gradient Zero By finding the slope of the. Y2), the slope of the line through these two. the gradient theorem is useful for example because it allows to get tangent planes and tangent lines very fast, faster than by. The slope of a vertical tangent line is. tangent lines are a fundamental concept in calculus that help us understand how. Tangent Line Gradient Zero.
From mathsathome.com
How to Find the Equation of a Tangent Line Tangent Line Gradient Zero By finding the slope of the. tangent lines are a fundamental concept in calculus that help us understand how a curve behaves at a single point. — in this section discuss how the gradient vector can be used to find tangent planes to a much more general. Given a differentiable function f and a point (x 0, y. Tangent Line Gradient Zero.
From www.expii.com
Sketching Derivatives Discontinuities, Cusps, and Tangents Expii Tangent Line Gradient Zero By finding the slope of the. The slope of a vertical tangent line is. — when dealing with a function \(y=f(x)\) of one variable, we stated that a line through \((c,f(c))\) was tangent to \(f\). the gradient theorem is useful for example because it allows to get tangent planes and tangent lines very fast, faster than by. . Tangent Line Gradient Zero.
From www.chegg.com
Solved a. Graph the function f(x) = x2 6x + 5. b. Identify Tangent Line Gradient Zero — when dealing with a function \(y=f(x)\) of one variable, we stated that a line through \((c,f(c))\) was tangent to \(f\). By finding the slope of the. — in this section discuss how the gradient vector can be used to find tangent planes to a much more general. The slope of a vertical tangent line is. tangent. Tangent Line Gradient Zero.
From www.youtube.com
Ex Determine the Intervals for Which the Slope of Tangent Lines is Tangent Line Gradient Zero The slope of a vertical tangent line is. — when dealing with a function \(y=f(x)\) of one variable, we stated that a line through \((c,f(c))\) was tangent to \(f\). By finding the slope of the. Given a differentiable function f and a point (x 0, y 0) the equation for the tangent line to the function f at (x. Tangent Line Gradient Zero.
From www.youtube.com
How to calculate the gradient of a curve gradient of a curve using a Tangent Line Gradient Zero — in this section discuss how the gradient vector can be used to find tangent planes to a much more general. Given a differentiable function f and a point (x 0, y 0) the equation for the tangent line to the function f at (x 0,. — when dealing with a function \(y=f(x)\) of one variable, we stated. Tangent Line Gradient Zero.
From www.numerade.com
SOLVED The graph below shows f(x). Determine whether the slope of the Tangent Line Gradient Zero tangent lines are a fundamental concept in calculus that help us understand how a curve behaves at a single point. By finding the slope of the. Y2), the slope of the line through these two. The slope of a vertical tangent line is. — when dealing with a function \(y=f(x)\) of one variable, we stated that a line. Tangent Line Gradient Zero.
From www.youtube.com
Lines Gradient and Relation with tangent Ratio of Slopes with Examples Tangent Line Gradient Zero Given a differentiable function f and a point (x 0, y 0) the equation for the tangent line to the function f at (x 0,. By finding the slope of the. the gradient theorem is useful for example because it allows to get tangent planes and tangent lines very fast, faster than by. Y2), the slope of the line. Tangent Line Gradient Zero.