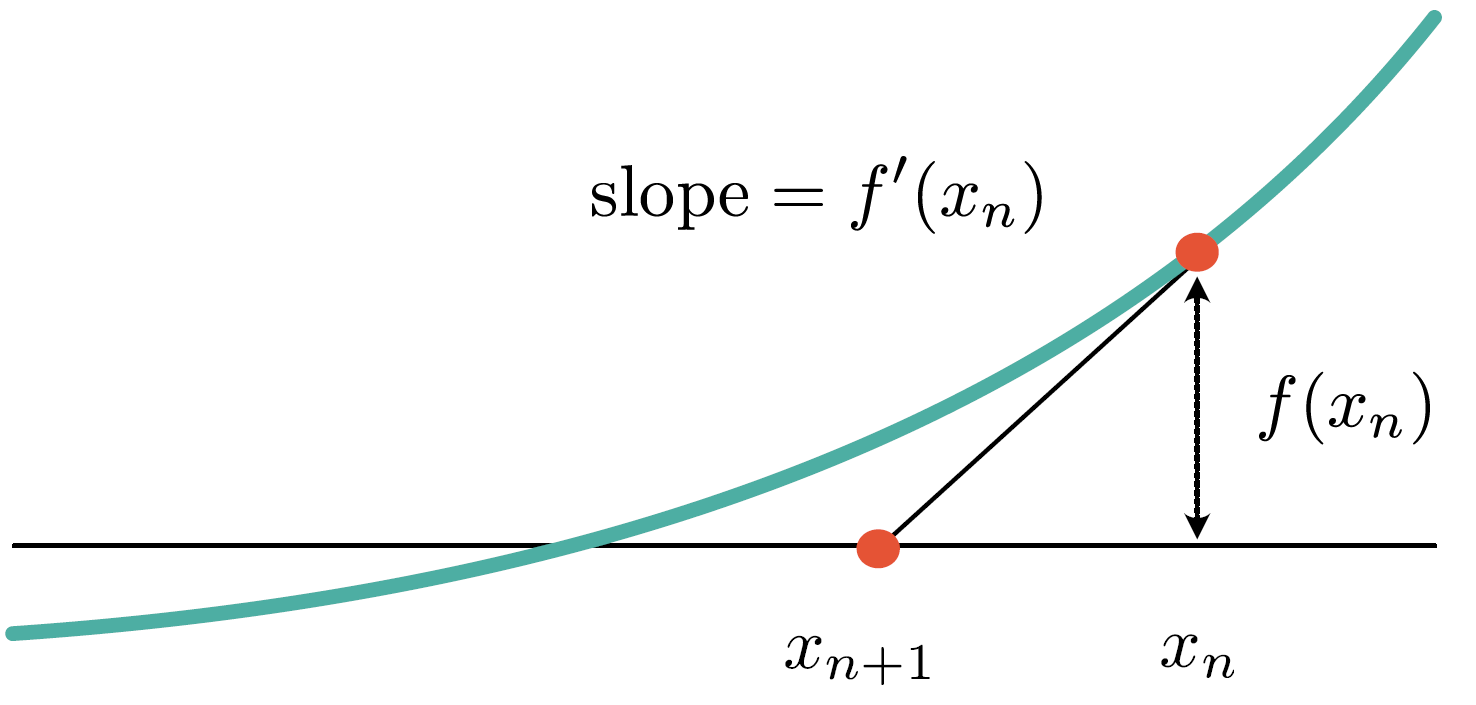
Newton Method Examples . Newton’s method is an iterative process that approximates numerical solutions or roots of an equation that's too hard to solve algebraically. Example 1 use newton’s method to determine an approximation to the solution to \(\cos x = x\) that lies in the interval \(\left[ {0,2}. In this case apply newton’s method to the derivative. Newton’s method approximates roots of [latex]f(x)=0[/latex] by starting with an initial approximation [latex]x_0[/latex], then uses tangent lines to the graph of [latex]f[/latex] to. Let’s work an example of newton’s method. Newton’s method can be used to find maxima and minima of functions in addition to the roots. Here is a set of practice problems to accompany the newton's method section of the applications of derivatives chapter of the notes. Newton's method applied to a quartic equation.
from www.eigenplus.com
Here is a set of practice problems to accompany the newton's method section of the applications of derivatives chapter of the notes. Example 1 use newton’s method to determine an approximation to the solution to \(\cos x = x\) that lies in the interval \(\left[ {0,2}. Newton’s method can be used to find maxima and minima of functions in addition to the roots. In this case apply newton’s method to the derivative. Newton's method applied to a quartic equation. Newton’s method approximates roots of [latex]f(x)=0[/latex] by starting with an initial approximation [latex]x_0[/latex], then uses tangent lines to the graph of [latex]f[/latex] to. Newton’s method is an iterative process that approximates numerical solutions or roots of an equation that's too hard to solve algebraically. Let’s work an example of newton’s method.
Newton Raphson Method Easy Graphical Illustration with example
Newton Method Examples In this case apply newton’s method to the derivative. Let’s work an example of newton’s method. Newton’s method is an iterative process that approximates numerical solutions or roots of an equation that's too hard to solve algebraically. Newton’s method can be used to find maxima and minima of functions in addition to the roots. Example 1 use newton’s method to determine an approximation to the solution to \(\cos x = x\) that lies in the interval \(\left[ {0,2}. Newton's method applied to a quartic equation. In this case apply newton’s method to the derivative. Newton’s method approximates roots of [latex]f(x)=0[/latex] by starting with an initial approximation [latex]x_0[/latex], then uses tangent lines to the graph of [latex]f[/latex] to. Here is a set of practice problems to accompany the newton's method section of the applications of derivatives chapter of the notes.
From www.slideserve.com
PPT Newton's Method PowerPoint Presentation, free download ID457655 Newton Method Examples Newton’s method is an iterative process that approximates numerical solutions or roots of an equation that's too hard to solve algebraically. Newton’s method approximates roots of [latex]f(x)=0[/latex] by starting with an initial approximation [latex]x_0[/latex], then uses tangent lines to the graph of [latex]f[/latex] to. Newton’s method can be used to find maxima and minima of functions in addition to the. Newton Method Examples.
From www.reddit.com
Newton's Method on Linear Approximation Examples Part 2 Where it Newton Method Examples Here is a set of practice problems to accompany the newton's method section of the applications of derivatives chapter of the notes. Newton's method applied to a quartic equation. Newton’s method is an iterative process that approximates numerical solutions or roots of an equation that's too hard to solve algebraically. Newton’s method approximates roots of [latex]f(x)=0[/latex] by starting with an. Newton Method Examples.
From twitter.com
MathType on Twitter "Newton’s method is a rootfinding algorithm that Newton Method Examples In this case apply newton’s method to the derivative. Let’s work an example of newton’s method. Newton's method applied to a quartic equation. Newton’s method can be used to find maxima and minima of functions in addition to the roots. Newton’s method is an iterative process that approximates numerical solutions or roots of an equation that's too hard to solve. Newton Method Examples.
From www.eigenplus.com
Newton Raphson Method Easy Graphical Illustration with example Newton Method Examples Newton's method applied to a quartic equation. Newton’s method can be used to find maxima and minima of functions in addition to the roots. Newton’s method approximates roots of [latex]f(x)=0[/latex] by starting with an initial approximation [latex]x_0[/latex], then uses tangent lines to the graph of [latex]f[/latex] to. Here is a set of practice problems to accompany the newton's method section. Newton Method Examples.
From study.com
Newton's Method in Calculus Formula, Equation & Examples Lesson Newton Method Examples Newton's method applied to a quartic equation. Here is a set of practice problems to accompany the newton's method section of the applications of derivatives chapter of the notes. Let’s work an example of newton’s method. Newton’s method approximates roots of [latex]f(x)=0[/latex] by starting with an initial approximation [latex]x_0[/latex], then uses tangent lines to the graph of [latex]f[/latex] to. Newton’s. Newton Method Examples.
From study.com
How to Use Newton's Method to Find Roots of Equations Video & Lesson Newton Method Examples Newton’s method can be used to find maxima and minima of functions in addition to the roots. Newton’s method approximates roots of [latex]f(x)=0[/latex] by starting with an initial approximation [latex]x_0[/latex], then uses tangent lines to the graph of [latex]f[/latex] to. Here is a set of practice problems to accompany the newton's method section of the applications of derivatives chapter of. Newton Method Examples.
From www.youtube.com
Newtons Method for Solving System of Equations With Newton Method Examples Let’s work an example of newton’s method. Here is a set of practice problems to accompany the newton's method section of the applications of derivatives chapter of the notes. Newton’s method approximates roots of [latex]f(x)=0[/latex] by starting with an initial approximation [latex]x_0[/latex], then uses tangent lines to the graph of [latex]f[/latex] to. Newton's method applied to a quartic equation. In. Newton Method Examples.
From www.youtube.com
Newton's Method Example 3 Numerical Computation YouTube Newton Method Examples Newton’s method approximates roots of [latex]f(x)=0[/latex] by starting with an initial approximation [latex]x_0[/latex], then uses tangent lines to the graph of [latex]f[/latex] to. In this case apply newton’s method to the derivative. Let’s work an example of newton’s method. Newton’s method is an iterative process that approximates numerical solutions or roots of an equation that's too hard to solve algebraically.. Newton Method Examples.
From www.youtube.com
Newton's method YouTube Newton Method Examples Newton’s method approximates roots of [latex]f(x)=0[/latex] by starting with an initial approximation [latex]x_0[/latex], then uses tangent lines to the graph of [latex]f[/latex] to. Newton’s method can be used to find maxima and minima of functions in addition to the roots. Example 1 use newton’s method to determine an approximation to the solution to \(\cos x = x\) that lies in. Newton Method Examples.
From www.youtube.com
Newton Raphson Method Examples YouTube Newton Method Examples Example 1 use newton’s method to determine an approximation to the solution to \(\cos x = x\) that lies in the interval \(\left[ {0,2}. Newton’s method can be used to find maxima and minima of functions in addition to the roots. Newton’s method is an iterative process that approximates numerical solutions or roots of an equation that's too hard to. Newton Method Examples.
From www.cuemath.com
Newton's Method Formula Learn Formula of Newton's Method Newton Method Examples Example 1 use newton’s method to determine an approximation to the solution to \(\cos x = x\) that lies in the interval \(\left[ {0,2}. In this case apply newton’s method to the derivative. Let’s work an example of newton’s method. Newton’s method can be used to find maxima and minima of functions in addition to the roots. Newton’s method is. Newton Method Examples.
From proper-cooking.info
Newtons Method Newton Method Examples Let’s work an example of newton’s method. In this case apply newton’s method to the derivative. Example 1 use newton’s method to determine an approximation to the solution to \(\cos x = x\) that lies in the interval \(\left[ {0,2}. Here is a set of practice problems to accompany the newton's method section of the applications of derivatives chapter of. Newton Method Examples.
From www.youtube.com
A Visual Representation of Newton's Method YouTube Newton Method Examples Let’s work an example of newton’s method. In this case apply newton’s method to the derivative. Newton’s method is an iterative process that approximates numerical solutions or roots of an equation that's too hard to solve algebraically. Newton’s method approximates roots of [latex]f(x)=0[/latex] by starting with an initial approximation [latex]x_0[/latex], then uses tangent lines to the graph of [latex]f[/latex] to.. Newton Method Examples.
From www.youtube.com
Newton's Method Examples Calculus JK Math YouTube Newton Method Examples Newton's method applied to a quartic equation. Newton’s method can be used to find maxima and minima of functions in addition to the roots. Here is a set of practice problems to accompany the newton's method section of the applications of derivatives chapter of the notes. Newton’s method approximates roots of [latex]f(x)=0[/latex] by starting with an initial approximation [latex]x_0[/latex], then. Newton Method Examples.
From www.slideserve.com
PPT Newton’s Method PowerPoint Presentation, free download ID2655300 Newton Method Examples Let’s work an example of newton’s method. Newton’s method can be used to find maxima and minima of functions in addition to the roots. Newton’s method is an iterative process that approximates numerical solutions or roots of an equation that's too hard to solve algebraically. In this case apply newton’s method to the derivative. Here is a set of practice. Newton Method Examples.
From www.youtube.com
Newton's Method Example YouTube Newton Method Examples Newton’s method is an iterative process that approximates numerical solutions or roots of an equation that's too hard to solve algebraically. Here is a set of practice problems to accompany the newton's method section of the applications of derivatives chapter of the notes. Newton’s method can be used to find maxima and minima of functions in addition to the roots.. Newton Method Examples.
From www.youtube.com
31 solve 3xcosx7=0 by newton's raphson method Working rule of Newton Method Examples Here is a set of practice problems to accompany the newton's method section of the applications of derivatives chapter of the notes. Newton’s method is an iterative process that approximates numerical solutions or roots of an equation that's too hard to solve algebraically. In this case apply newton’s method to the derivative. Example 1 use newton’s method to determine an. Newton Method Examples.
From www.youtube.com
Newton's Method for constrained optimization problems YouTube Newton Method Examples Newton’s method is an iterative process that approximates numerical solutions or roots of an equation that's too hard to solve algebraically. In this case apply newton’s method to the derivative. Here is a set of practice problems to accompany the newton's method section of the applications of derivatives chapter of the notes. Newton’s method can be used to find maxima. Newton Method Examples.
From calcworkshop.com
Newton's Method Newton Method Examples In this case apply newton’s method to the derivative. Example 1 use newton’s method to determine an approximation to the solution to \(\cos x = x\) that lies in the interval \(\left[ {0,2}. Newton’s method can be used to find maxima and minima of functions in addition to the roots. Let’s work an example of newton’s method. Here is a. Newton Method Examples.
From www.eigenplus.com
Newton Raphson Method Easy Graphical Illustration with example Newton Method Examples In this case apply newton’s method to the derivative. Newton’s method approximates roots of [latex]f(x)=0[/latex] by starting with an initial approximation [latex]x_0[/latex], then uses tangent lines to the graph of [latex]f[/latex] to. Newton's method applied to a quartic equation. Newton’s method can be used to find maxima and minima of functions in addition to the roots. Example 1 use newton’s. Newton Method Examples.
From www.youtube.com
Using Excel Newtons Method YouTube Newton Method Examples Newton’s method can be used to find maxima and minima of functions in addition to the roots. Let’s work an example of newton’s method. Newton's method applied to a quartic equation. Example 1 use newton’s method to determine an approximation to the solution to \(\cos x = x\) that lies in the interval \(\left[ {0,2}. Here is a set of. Newton Method Examples.
From www.youtube.com
Newton's Method YouTube Newton Method Examples Newton's method applied to a quartic equation. Newton’s method approximates roots of [latex]f(x)=0[/latex] by starting with an initial approximation [latex]x_0[/latex], then uses tangent lines to the graph of [latex]f[/latex] to. Let’s work an example of newton’s method. Here is a set of practice problems to accompany the newton's method section of the applications of derivatives chapter of the notes. Newton’s. Newton Method Examples.
From www.math.ucdavis.edu
Newton's Method Newton Method Examples Newton's method applied to a quartic equation. Let’s work an example of newton’s method. Newton’s method is an iterative process that approximates numerical solutions or roots of an equation that's too hard to solve algebraically. In this case apply newton’s method to the derivative. Newton’s method can be used to find maxima and minima of functions in addition to the. Newton Method Examples.
From www.youtube.com
05 Newton's Method of Approximation Part1 YouTube Newton Method Examples In this case apply newton’s method to the derivative. Let’s work an example of newton’s method. Newton’s method can be used to find maxima and minima of functions in addition to the roots. Newton’s method is an iterative process that approximates numerical solutions or roots of an equation that's too hard to solve algebraically. Newton's method applied to a quartic. Newton Method Examples.
From www.youtube.com
Newton Raphson Method Newton Raphson Method Example YouTube Newton Method Examples Here is a set of practice problems to accompany the newton's method section of the applications of derivatives chapter of the notes. Let’s work an example of newton’s method. Newton's method applied to a quartic equation. Newton’s method is an iterative process that approximates numerical solutions or roots of an equation that's too hard to solve algebraically. Newton’s method approximates. Newton Method Examples.
From www.slideserve.com
PPT A brief history of Newton’s method PowerPoint Presentation, free Newton Method Examples Newton’s method can be used to find maxima and minima of functions in addition to the roots. Here is a set of practice problems to accompany the newton's method section of the applications of derivatives chapter of the notes. In this case apply newton’s method to the derivative. Example 1 use newton’s method to determine an approximation to the solution. Newton Method Examples.
From www.showme.com
Newton Raphson method example Math, Numerical Methods, Newton Method Examples Newton’s method approximates roots of [latex]f(x)=0[/latex] by starting with an initial approximation [latex]x_0[/latex], then uses tangent lines to the graph of [latex]f[/latex] to. In this case apply newton’s method to the derivative. Here is a set of practice problems to accompany the newton's method section of the applications of derivatives chapter of the notes. Newton's method applied to a quartic. Newton Method Examples.
From www.youtube.com
Newton Raphson Method for Numerical Solution of Equations Calculus Newton Method Examples In this case apply newton’s method to the derivative. Newton’s method approximates roots of [latex]f(x)=0[/latex] by starting with an initial approximation [latex]x_0[/latex], then uses tangent lines to the graph of [latex]f[/latex] to. Example 1 use newton’s method to determine an approximation to the solution to \(\cos x = x\) that lies in the interval \(\left[ {0,2}. Let’s work an example. Newton Method Examples.
From calcworkshop.com
Newton's Method (How To w/ StepbyStep Examples!) Newton Method Examples Newton’s method approximates roots of [latex]f(x)=0[/latex] by starting with an initial approximation [latex]x_0[/latex], then uses tangent lines to the graph of [latex]f[/latex] to. Let’s work an example of newton’s method. In this case apply newton’s method to the derivative. Example 1 use newton’s method to determine an approximation to the solution to \(\cos x = x\) that lies in the. Newton Method Examples.
From www.youtube.com
Newton's Method YouTube Newton Method Examples In this case apply newton’s method to the derivative. Newton’s method approximates roots of [latex]f(x)=0[/latex] by starting with an initial approximation [latex]x_0[/latex], then uses tangent lines to the graph of [latex]f[/latex] to. Let’s work an example of newton’s method. Newton's method applied to a quartic equation. Newton’s method is an iterative process that approximates numerical solutions or roots of an. Newton Method Examples.
From www.youtube.com
NEWTON RAPHSON METHOD ONLINE LECTURES,YEAR SOLUTION Newton Method Examples Newton's method applied to a quartic equation. In this case apply newton’s method to the derivative. Example 1 use newton’s method to determine an approximation to the solution to \(\cos x = x\) that lies in the interval \(\left[ {0,2}. Newton’s method is an iterative process that approximates numerical solutions or roots of an equation that's too hard to solve. Newton Method Examples.
From www.youtube.com
STPM , NewtonRaphson Method. Introduction and Example. YouTube Newton Method Examples Newton's method applied to a quartic equation. Here is a set of practice problems to accompany the newton's method section of the applications of derivatives chapter of the notes. Newton’s method can be used to find maxima and minima of functions in addition to the roots. Example 1 use newton’s method to determine an approximation to the solution to \(\cos. Newton Method Examples.
From www.slideserve.com
PPT Chapter 6 Roots Open Methods PowerPoint Presentation, free Newton Method Examples Newton’s method can be used to find maxima and minima of functions in addition to the roots. Newton’s method approximates roots of [latex]f(x)=0[/latex] by starting with an initial approximation [latex]x_0[/latex], then uses tangent lines to the graph of [latex]f[/latex] to. Newton's method applied to a quartic equation. In this case apply newton’s method to the derivative. Example 1 use newton’s. Newton Method Examples.
From www.youtube.com
Newton's Method YouTube Newton Method Examples Newton’s method can be used to find maxima and minima of functions in addition to the roots. In this case apply newton’s method to the derivative. Newton’s method approximates roots of [latex]f(x)=0[/latex] by starting with an initial approximation [latex]x_0[/latex], then uses tangent lines to the graph of [latex]f[/latex] to. Here is a set of practice problems to accompany the newton's. Newton Method Examples.
From mr-mathematics.com
NewtonRaphson Method Newton Method Examples Newton’s method approximates roots of [latex]f(x)=0[/latex] by starting with an initial approximation [latex]x_0[/latex], then uses tangent lines to the graph of [latex]f[/latex] to. Here is a set of practice problems to accompany the newton's method section of the applications of derivatives chapter of the notes. Newton's method applied to a quartic equation. Let’s work an example of newton’s method. In. Newton Method Examples.