Non Standard Inner Product . An inner product is a generalization of the dot product. Let v = ir2, and fe1;e2g be the standard basis. The euclidean inner product in ir2. Given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let. New inner products from old. A vector space endowed with a norm is called a normed vector space, or simply a normed space. Given two arbitrary vectors x = x1e1 + x2e2 and y = y1e1 + y2e2, then (x;y) = x1y1 + x2y2: Defines an inner product on \(\mathbb{r}^n\), and every inner product on \(\mathbb{r}^n\) arises in this way. In a vector space, it is a way to multiply vectors together, with the result of this. A positive map m > 0 de nes a nonstandard inner product h ; An important fact about norms is that they. Let x be a vector space with inner product ( ;
from www.numerade.com
New inner products from old. Let v = ir2, and fe1;e2g be the standard basis. A vector space endowed with a norm is called a normed vector space, or simply a normed space. A positive map m > 0 de nes a nonstandard inner product h ; The euclidean inner product in ir2. Defines an inner product on \(\mathbb{r}^n\), and every inner product on \(\mathbb{r}^n\) arises in this way. Given two arbitrary vectors x = x1e1 + x2e2 and y = y1e1 + y2e2, then (x;y) = x1y1 + x2y2: Given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let. An important fact about norms is that they. Let x be a vector space with inner product ( ;
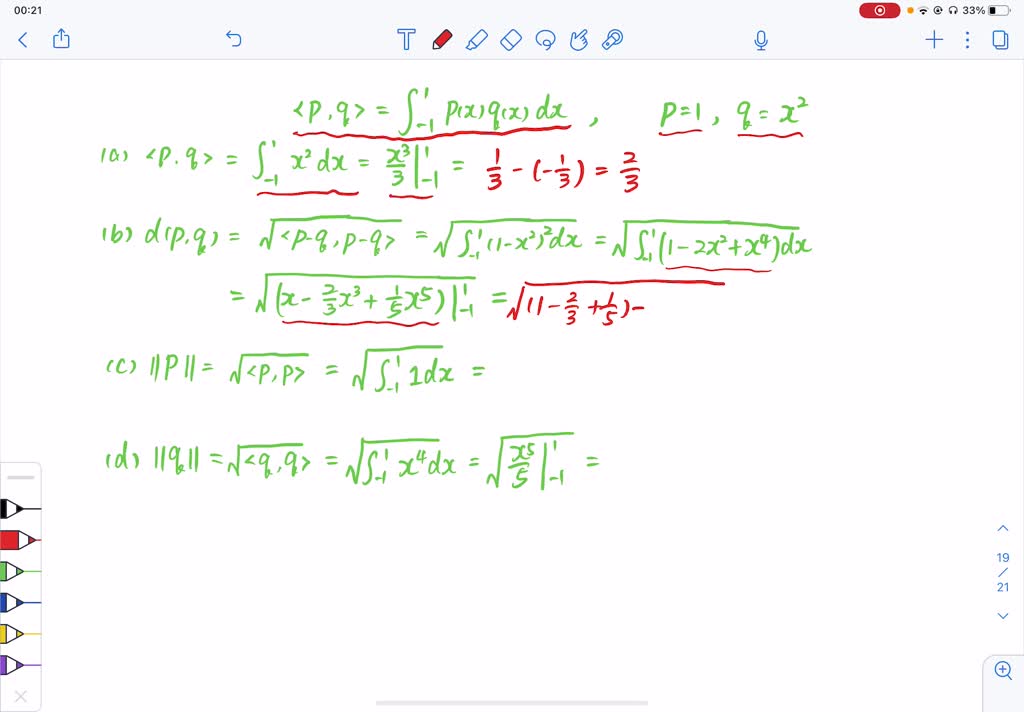
SOLVED(Calculus required) Let the vector space P2 have the inner
Non Standard Inner Product New inner products from old. Let x be a vector space with inner product ( ; The euclidean inner product in ir2. An inner product is a generalization of the dot product. Given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let. Let v = ir2, and fe1;e2g be the standard basis. An important fact about norms is that they. A positive map m > 0 de nes a nonstandard inner product h ; Defines an inner product on \(\mathbb{r}^n\), and every inner product on \(\mathbb{r}^n\) arises in this way. Given two arbitrary vectors x = x1e1 + x2e2 and y = y1e1 + y2e2, then (x;y) = x1y1 + x2y2: In a vector space, it is a way to multiply vectors together, with the result of this. New inner products from old. A vector space endowed with a norm is called a normed vector space, or simply a normed space.
From www.slideserve.com
PPT Quantum Computation PowerPoint Presentation, free download ID Non Standard Inner Product An inner product is a generalization of the dot product. A vector space endowed with a norm is called a normed vector space, or simply a normed space. In a vector space, it is a way to multiply vectors together, with the result of this. New inner products from old. Given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let. An important. Non Standard Inner Product.
From www.chegg.com
Solved Let V = R2, equipped with the nonstandard inner Non Standard Inner Product An inner product is a generalization of the dot product. A positive map m > 0 de nes a nonstandard inner product h ; In a vector space, it is a way to multiply vectors together, with the result of this. Given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let. The euclidean inner product in ir2. Let v = ir2, and. Non Standard Inner Product.
From www.semanticscholar.org
Figure 2 from Householder orthogonalization with a nonstandard inner Non Standard Inner Product New inner products from old. In a vector space, it is a way to multiply vectors together, with the result of this. Defines an inner product on \(\mathbb{r}^n\), and every inner product on \(\mathbb{r}^n\) arises in this way. Given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let. Let v = ir2, and fe1;e2g be the standard basis. Given two arbitrary vectors. Non Standard Inner Product.
From link.springer.com
Efficient implementations of the modified GramSchmidt Non Standard Inner Product Given two arbitrary vectors x = x1e1 + x2e2 and y = y1e1 + y2e2, then (x;y) = x1y1 + x2y2: Let x be a vector space with inner product ( ; A vector space endowed with a norm is called a normed vector space, or simply a normed space. In a vector space, it is a way to multiply. Non Standard Inner Product.
From www.youtube.com
Linear Algebra Inner Product YouTube Non Standard Inner Product Defines an inner product on \(\mathbb{r}^n\), and every inner product on \(\mathbb{r}^n\) arises in this way. Given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let. A vector space endowed with a norm is called a normed vector space, or simply a normed space. An important fact about norms is that they. Let x be a vector space with inner product (. Non Standard Inner Product.
From www.youtube.com
Linear Algebra 33 Transpose and Inner Product YouTube Non Standard Inner Product Let v = ir2, and fe1;e2g be the standard basis. A vector space endowed with a norm is called a normed vector space, or simply a normed space. A positive map m > 0 de nes a nonstandard inner product h ; Let x be a vector space with inner product ( ; Defines an inner product on \(\mathbb{r}^n\), and. Non Standard Inner Product.
From yishang.en.made-in-china.com
Customized NonStandard Inner Support Radiator Chassis Rack Sheet Metal Non Standard Inner Product Let v = ir2, and fe1;e2g be the standard basis. The euclidean inner product in ir2. An inner product is a generalization of the dot product. Given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let. A vector space endowed with a norm is called a normed vector space, or simply a normed space. Given two arbitrary vectors x = x1e1 +. Non Standard Inner Product.
From deepai.org
Householder orthogonalization with a nonstandard inner product DeepAI Non Standard Inner Product Let x be a vector space with inner product ( ; The euclidean inner product in ir2. An important fact about norms is that they. In a vector space, it is a way to multiply vectors together, with the result of this. A vector space endowed with a norm is called a normed vector space, or simply a normed space.. Non Standard Inner Product.
From www.chegg.com
Solved The vector space R3 is made an inner product space V Non Standard Inner Product A positive map m > 0 de nes a nonstandard inner product h ; An inner product is a generalization of the dot product. New inner products from old. The euclidean inner product in ir2. Given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let. Let x be a vector space with inner product ( ; A vector space endowed with a. Non Standard Inner Product.
From www.youtube.com
Inner Product Spaces YouTube Non Standard Inner Product Defines an inner product on \(\mathbb{r}^n\), and every inner product on \(\mathbb{r}^n\) arises in this way. The euclidean inner product in ir2. In a vector space, it is a way to multiply vectors together, with the result of this. Given two arbitrary vectors x = x1e1 + x2e2 and y = y1e1 + y2e2, then (x;y) = x1y1 + x2y2:. Non Standard Inner Product.
From www.youtube.com
Inner Products YouTube Non Standard Inner Product Given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let. Let v = ir2, and fe1;e2g be the standard basis. The euclidean inner product in ir2. An inner product is a generalization of the dot product. New inner products from old. Given two arbitrary vectors x = x1e1 + x2e2 and y = y1e1 + y2e2, then (x;y) = x1y1 + x2y2:. Non Standard Inner Product.
From www.slideserve.com
PPT Chapter 5 Inner Product Spaces PowerPoint Presentation, free Non Standard Inner Product The euclidean inner product in ir2. Given two arbitrary vectors x = x1e1 + x2e2 and y = y1e1 + y2e2, then (x;y) = x1y1 + x2y2: Given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let. A vector space endowed with a norm is called a normed vector space, or simply a normed space. In a vector space, it is a. Non Standard Inner Product.
From www.youtube.com
Representation Theory 6, Standard Inner Product, Orthogonal and Non Standard Inner Product New inner products from old. In a vector space, it is a way to multiply vectors together, with the result of this. A vector space endowed with a norm is called a normed vector space, or simply a normed space. The euclidean inner product in ir2. Let v = ir2, and fe1;e2g be the standard basis. A positive map m. Non Standard Inner Product.
From www.researchgate.net
(PDF) Numerical stability of orthogonalization methods with a non Non Standard Inner Product In a vector space, it is a way to multiply vectors together, with the result of this. Defines an inner product on \(\mathbb{r}^n\), and every inner product on \(\mathbb{r}^n\) arises in this way. An inner product is a generalization of the dot product. A positive map m > 0 de nes a nonstandard inner product h ; An important fact. Non Standard Inner Product.
From www.chegg.com
Solved > 1 Equipe the coordinate space RS with the weighted Non Standard Inner Product A positive map m > 0 de nes a nonstandard inner product h ; Given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let. In a vector space, it is a way to multiply vectors together, with the result of this. Let v = ir2, and fe1;e2g be the standard basis. Let x be a vector space with inner product ( ;. Non Standard Inner Product.
From www.slideserve.com
PPT CHAPTER 5 INNER PRODUCT SPACES PowerPoint Presentation, free Non Standard Inner Product An important fact about norms is that they. Given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let. New inner products from old. A positive map m > 0 de nes a nonstandard inner product h ; Let x be a vector space with inner product ( ; A vector space endowed with a norm is called a normed vector space, or. Non Standard Inner Product.
From www.chegg.com
Solved Let V =R, equipped with the nonstandard inner Non Standard Inner Product Defines an inner product on \(\mathbb{r}^n\), and every inner product on \(\mathbb{r}^n\) arises in this way. An inner product is a generalization of the dot product. An important fact about norms is that they. In a vector space, it is a way to multiply vectors together, with the result of this. A vector space endowed with a norm is called. Non Standard Inner Product.
From www.chegg.com
Solved 4. The standard inner product on R” can be Non Standard Inner Product Given two arbitrary vectors x = x1e1 + x2e2 and y = y1e1 + y2e2, then (x;y) = x1y1 + x2y2: Let v = ir2, and fe1;e2g be the standard basis. An important fact about norms is that they. A positive map m > 0 de nes a nonstandard inner product h ; Defines an inner product on \(\mathbb{r}^n\), and. Non Standard Inner Product.
From www.slideserve.com
PPT Chapter 7 Inner Product Spaces PowerPoint Presentation, free Non Standard Inner Product An important fact about norms is that they. An inner product is a generalization of the dot product. A vector space endowed with a norm is called a normed vector space, or simply a normed space. Given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let. In a vector space, it is a way to multiply vectors together, with the result of. Non Standard Inner Product.
From www.slideserve.com
PPT Chapter 3 Linear Algebra Review and Elementary Differential Non Standard Inner Product New inner products from old. A positive map m > 0 de nes a nonstandard inner product h ; Let v = ir2, and fe1;e2g be the standard basis. The euclidean inner product in ir2. An important fact about norms is that they. Defines an inner product on \(\mathbb{r}^n\), and every inner product on \(\mathbb{r}^n\) arises in this way. In. Non Standard Inner Product.
From www.youtube.com
Inner product vs dot product YouTube Non Standard Inner Product Given two arbitrary vectors x = x1e1 + x2e2 and y = y1e1 + y2e2, then (x;y) = x1y1 + x2y2: In a vector space, it is a way to multiply vectors together, with the result of this. Let x be a vector space with inner product ( ; Let v = ir2, and fe1;e2g be the standard basis. New. Non Standard Inner Product.
From www.chegg.com
Solved In Exercises 910, compute the standard inner product Non Standard Inner Product Given two arbitrary vectors x = x1e1 + x2e2 and y = y1e1 + y2e2, then (x;y) = x1y1 + x2y2: Defines an inner product on \(\mathbb{r}^n\), and every inner product on \(\mathbb{r}^n\) arises in this way. Let v = ir2, and fe1;e2g be the standard basis. A vector space endowed with a norm is called a normed vector space,. Non Standard Inner Product.
From www.chegg.com
Solved Let ( ) be thw standard inner product on R^2, and Non Standard Inner Product A positive map m > 0 de nes a nonstandard inner product h ; An important fact about norms is that they. An inner product is a generalization of the dot product. Defines an inner product on \(\mathbb{r}^n\), and every inner product on \(\mathbb{r}^n\) arises in this way. New inner products from old. Let v = ir2, and fe1;e2g be. Non Standard Inner Product.
From www.semanticscholar.org
Table 1 from Rounding error analysis of orthogonalization with a non Non Standard Inner Product An important fact about norms is that they. In a vector space, it is a way to multiply vectors together, with the result of this. A positive map m > 0 de nes a nonstandard inner product h ; An inner product is a generalization of the dot product. Let x be a vector space with inner product ( ;. Non Standard Inner Product.
From slideplayer.com
Inner Product, Length and Orthogonality ppt download Non Standard Inner Product Let v = ir2, and fe1;e2g be the standard basis. Defines an inner product on \(\mathbb{r}^n\), and every inner product on \(\mathbb{r}^n\) arises in this way. The euclidean inner product in ir2. A positive map m > 0 de nes a nonstandard inner product h ; Let x be a vector space with inner product ( ; Given an inner. Non Standard Inner Product.
From studylib.net
Inner Product Space Non Standard Inner Product A vector space endowed with a norm is called a normed vector space, or simply a normed space. An inner product is a generalization of the dot product. A positive map m > 0 de nes a nonstandard inner product h ; Let x be a vector space with inner product ( ; Defines an inner product on \(\mathbb{r}^n\), and. Non Standard Inner Product.
From www.slideserve.com
PPT Inner Product PowerPoint Presentation, free download ID2663418 Non Standard Inner Product Given two arbitrary vectors x = x1e1 + x2e2 and y = y1e1 + y2e2, then (x;y) = x1y1 + x2y2: The euclidean inner product in ir2. An inner product is a generalization of the dot product. Let v = ir2, and fe1;e2g be the standard basis. In a vector space, it is a way to multiply vectors together, with. Non Standard Inner Product.
From www.deep-mind.org
Inner Products, Norms and Metrics deep mind Non Standard Inner Product An inner product is a generalization of the dot product. The euclidean inner product in ir2. In a vector space, it is a way to multiply vectors together, with the result of this. An important fact about norms is that they. Given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let. Let x be a vector space with inner product ( ;. Non Standard Inner Product.
From www.youtube.com
Use a nonstandard inner product in R^3 YouTube Non Standard Inner Product Let x be a vector space with inner product ( ; An inner product is a generalization of the dot product. Defines an inner product on \(\mathbb{r}^n\), and every inner product on \(\mathbb{r}^n\) arises in this way. An important fact about norms is that they. New inner products from old. A positive map m > 0 de nes a nonstandard. Non Standard Inner Product.
From math.stackexchange.com
linear algebra Can anyone help provide an additional example of Non Standard Inner Product New inner products from old. In a vector space, it is a way to multiply vectors together, with the result of this. An important fact about norms is that they. An inner product is a generalization of the dot product. Defines an inner product on \(\mathbb{r}^n\), and every inner product on \(\mathbb{r}^n\) arises in this way. Given two arbitrary vectors. Non Standard Inner Product.
From www.chegg.com
Solved Equipe the coordinate space R4 with the weighted (or Non Standard Inner Product An important fact about norms is that they. Let v = ir2, and fe1;e2g be the standard basis. Given two arbitrary vectors x = x1e1 + x2e2 and y = y1e1 + y2e2, then (x;y) = x1y1 + x2y2: In a vector space, it is a way to multiply vectors together, with the result of this. Defines an inner product. Non Standard Inner Product.
From www.pinterest.co.uk
Épinglé sur Algebra Non Standard Inner Product Let x be a vector space with inner product ( ; New inner products from old. An inner product is a generalization of the dot product. An important fact about norms is that they. Let v = ir2, and fe1;e2g be the standard basis. A vector space endowed with a norm is called a normed vector space, or simply a. Non Standard Inner Product.
From www.slideserve.com
PPT Chapter 7 Inner Product Spaces PowerPoint Presentation, free Non Standard Inner Product An important fact about norms is that they. In a vector space, it is a way to multiply vectors together, with the result of this. A vector space endowed with a norm is called a normed vector space, or simply a normed space. An inner product is a generalization of the dot product. The euclidean inner product in ir2. Let. Non Standard Inner Product.
From www.vrogue.co
Dot Product Inner Product vrogue.co Non Standard Inner Product A vector space endowed with a norm is called a normed vector space, or simply a normed space. New inner products from old. Given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let. An important fact about norms is that they. Let x be a vector space with inner product ( ; In a vector space, it is a way to multiply. Non Standard Inner Product.
From www.numerade.com
SOLVED(Calculus required) Let the vector space P2 have the inner Non Standard Inner Product Given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let. Let v = ir2, and fe1;e2g be the standard basis. A positive map m > 0 de nes a nonstandard inner product h ; In a vector space, it is a way to multiply vectors together, with the result of this. A vector space endowed with a norm is called a normed. Non Standard Inner Product.