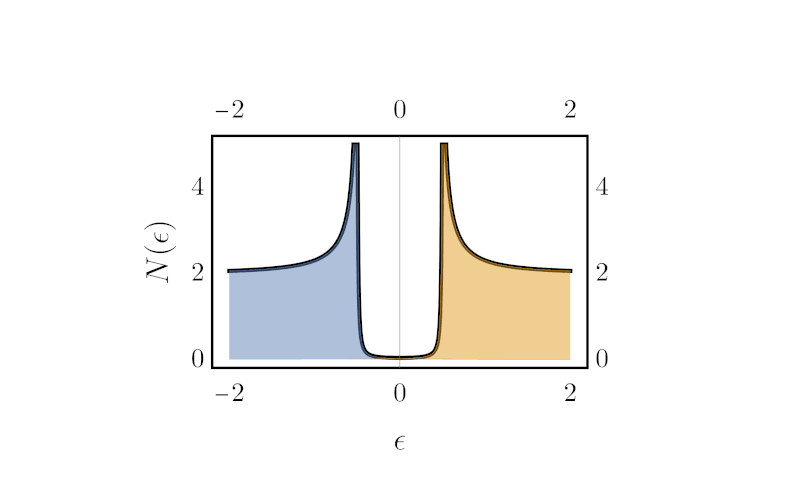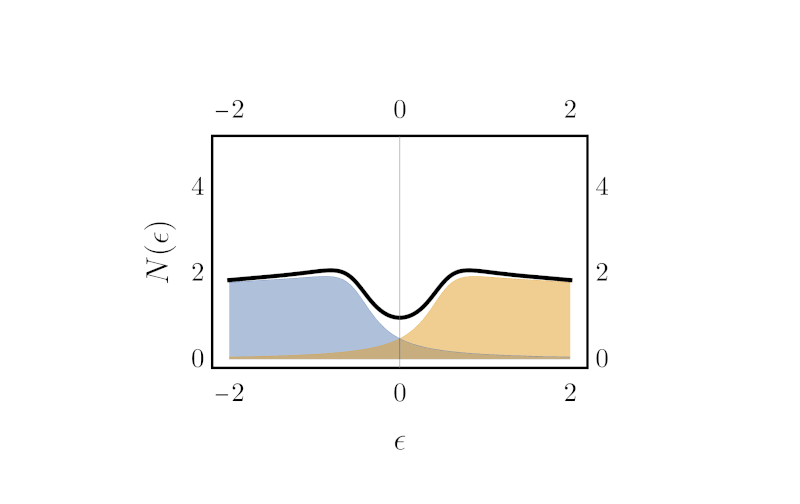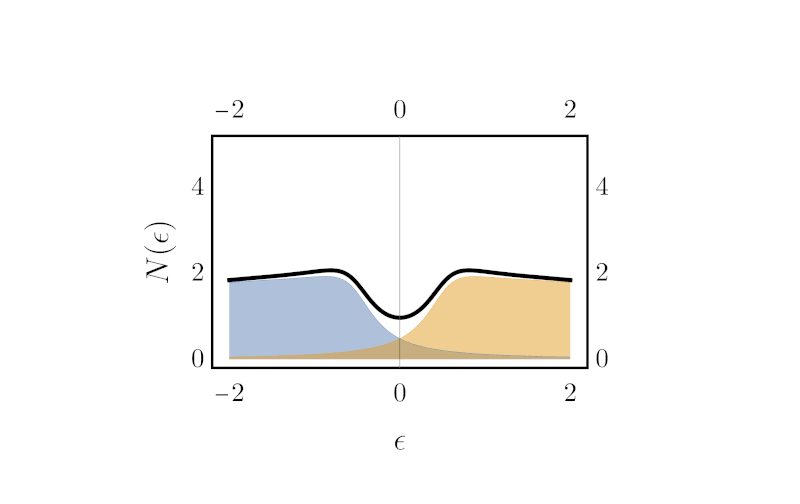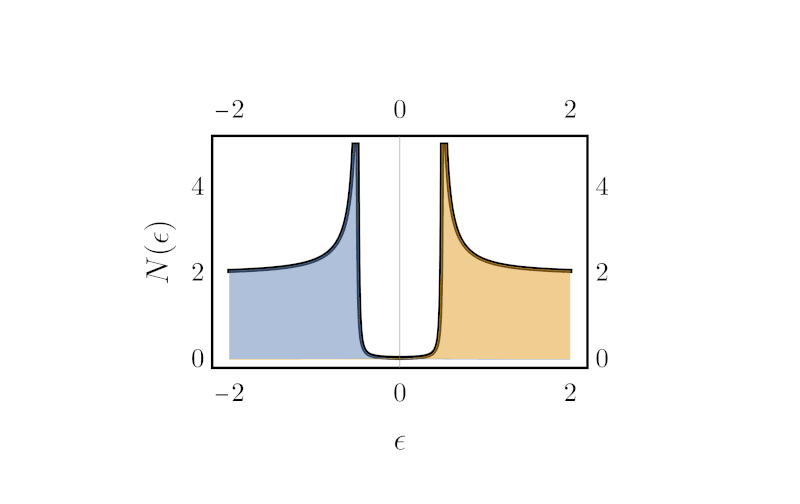
Green S Functions at Seth Struth blog

Green S Functions. That is, the green’s function for a domain ω 1⁄2 rn is the function defined as. We will now consider initial value and boundary value problems. If such a representation exists, the kernel of this integral operator g(x; To find the green’s function for a 2d domain d, we first find the simplest function that satisfies ∇ 2 v = δ(r). Y) = φ(y ¡ x) ¡. Each type of problem will lead to a solution of the form. Y(x) = c1y1(x) + c2y2(x) + ∫b. We define this function g as the green’s function for ω. It is useful to give a physical. The function \ (g (x, \xi)\) is referred to as the kernel of the integral operator and is called the green’s function. A green’s function is a solution to an inhomogenous diferential equation with a delta function “driving term”. X0) is called the green’s function. Generally speaking, a green's function is an integral kernel that can be used to solve differential equations from a large number of families including simpler examples such as. It provides a convenient method for solving.

X0) is called the green’s function. If such a representation exists, the kernel of this integral operator g(x; It is useful to give a physical. Y(x) = c1y1(x) + c2y2(x) + ∫b. To find the green’s function for a 2d domain d, we first find the simplest function that satisfies ∇ 2 v = δ(r). It provides a convenient method for solving. Each type of problem will lead to a solution of the form. Generally speaking, a green's function is an integral kernel that can be used to solve differential equations from a large number of families including simpler examples such as. Y) = φ(y ¡ x) ¡. We define this function g as the green’s function for ω.

Visual Introduction to Green’s Functions Simon Verret’s

Green S Functions It is useful to give a physical. X0) is called the green’s function. It provides a convenient method for solving. If such a representation exists, the kernel of this integral operator g(x; Each type of problem will lead to a solution of the form. To find the green’s function for a 2d domain d, we first find the simplest function that satisfies ∇ 2 v = δ(r). A green’s function is a solution to an inhomogenous diferential equation with a delta function “driving term”. That is, the green’s function for a domain ω 1⁄2 rn is the function defined as. It is useful to give a physical. Y(x) = c1y1(x) + c2y2(x) + ∫b. Generally speaking, a green's function is an integral kernel that can be used to solve differential equations from a large number of families including simpler examples such as. The function \ (g (x, \xi)\) is referred to as the kernel of the integral operator and is called the green’s function. We will now consider initial value and boundary value problems. Y) = φ(y ¡ x) ¡. We define this function g as the green’s function for ω.