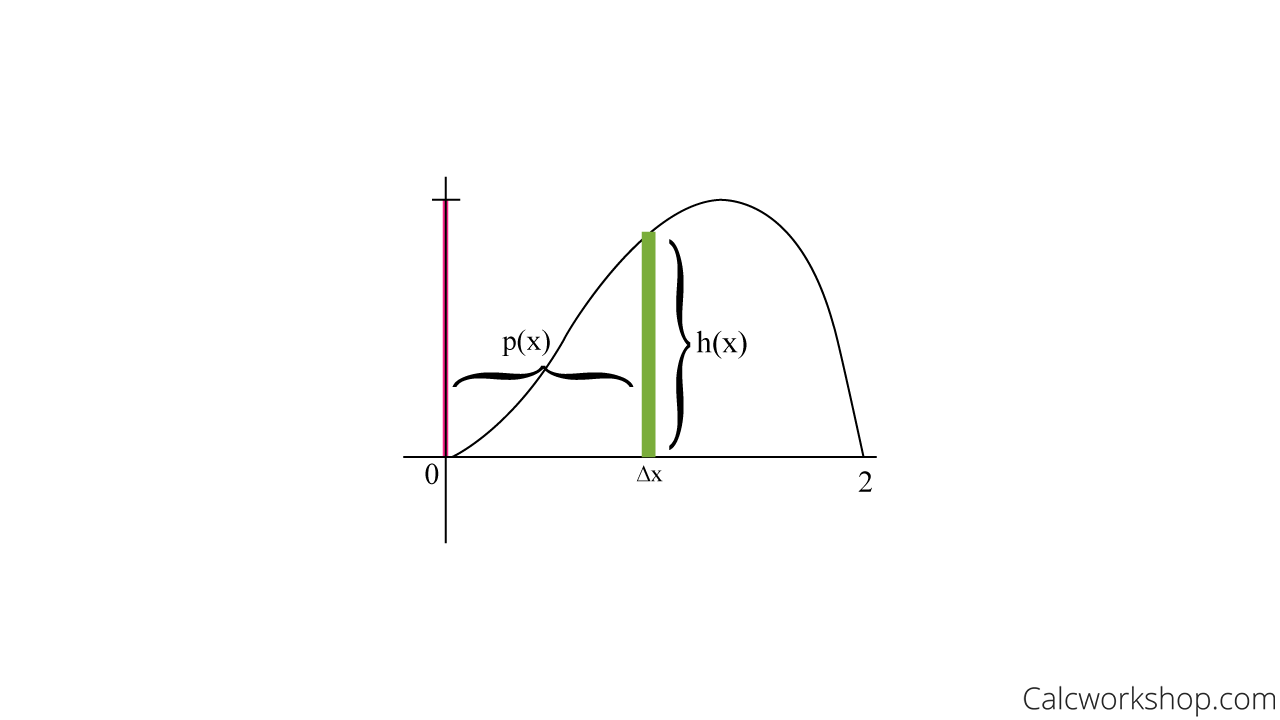Shell Method Rules . 9.4 volumes of solids of revolution: Let r be the region under the curve y = f (x) between x = a and x = b (0 ≤ a <b) (figure 1. The shell method is a method of finding volumes by decomposing a solid of revolution into cylindrical shells. Instead of slicing the solid perpendicular to the. Here’s how you use the shell method, step by step, to find the volume of the can: This section develops another method of computing volume, the shell method. However, we provide a general guideline. Compare the different methods for calculating a volume of revolution. Consider a region in the plane that is divided into thin vertical strips. Calculate the volume of a solid of revolution by using the method of cylindrical shells. Find an expression that represents the area of a random shell of the can (in terms of x):. There are many different scenarios in which the shell method can be employed, which are not discussed here;
from calcworkshop.com
Let r be the region under the curve y = f (x) between x = a and x = b (0 ≤ a <b) (figure 1. Here’s how you use the shell method, step by step, to find the volume of the can: Compare the different methods for calculating a volume of revolution. Instead of slicing the solid perpendicular to the. However, we provide a general guideline. Find an expression that represents the area of a random shell of the can (in terms of x):. Consider a region in the plane that is divided into thin vertical strips. The shell method is a method of finding volumes by decomposing a solid of revolution into cylindrical shells. There are many different scenarios in which the shell method can be employed, which are not discussed here; 9.4 volumes of solids of revolution:
How To Use The Shell Method? (w/ 3 Powerful Examples!)
Shell Method Rules However, we provide a general guideline. Consider a region in the plane that is divided into thin vertical strips. Let r be the region under the curve y = f (x) between x = a and x = b (0 ≤ a <b) (figure 1. 9.4 volumes of solids of revolution: Find an expression that represents the area of a random shell of the can (in terms of x):. Compare the different methods for calculating a volume of revolution. There are many different scenarios in which the shell method can be employed, which are not discussed here; Instead of slicing the solid perpendicular to the. Calculate the volume of a solid of revolution by using the method of cylindrical shells. The shell method is a method of finding volumes by decomposing a solid of revolution into cylindrical shells. Here’s how you use the shell method, step by step, to find the volume of the can: This section develops another method of computing volume, the shell method. However, we provide a general guideline.
From medium.com
Shell Method. Shell Method is particularly good for… by Solomon Xie Shell Method Rules This section develops another method of computing volume, the shell method. Find an expression that represents the area of a random shell of the can (in terms of x):. There are many different scenarios in which the shell method can be employed, which are not discussed here; The shell method is a method of finding volumes by decomposing a solid. Shell Method Rules.
From www.youtube.com
Volume by Shell Method finding the radius YouTube Shell Method Rules This section develops another method of computing volume, the shell method. The shell method is a method of finding volumes by decomposing a solid of revolution into cylindrical shells. Consider a region in the plane that is divided into thin vertical strips. Calculate the volume of a solid of revolution by using the method of cylindrical shells. Instead of slicing. Shell Method Rules.
From www.youtube.com
Shell method with two functions of x AP Calculus AB Khan Academy Shell Method Rules This section develops another method of computing volume, the shell method. The shell method is a method of finding volumes by decomposing a solid of revolution into cylindrical shells. 9.4 volumes of solids of revolution: Instead of slicing the solid perpendicular to the. Find an expression that represents the area of a random shell of the can (in terms of. Shell Method Rules.
From www.youtube.com
The Shell Method Calculus 2 Lesson 4 JK Math YouTube Shell Method Rules The shell method is a method of finding volumes by decomposing a solid of revolution into cylindrical shells. This section develops another method of computing volume, the shell method. Find an expression that represents the area of a random shell of the can (in terms of x):. Instead of slicing the solid perpendicular to the. Compare the different methods for. Shell Method Rules.
From echayunx.blogspot.com
√ Shell Method Formula 6 3 Volumes Of Revolution The Shell Method Shell Method Rules Instead of slicing the solid perpendicular to the. Calculate the volume of a solid of revolution by using the method of cylindrical shells. Find an expression that represents the area of a random shell of the can (in terms of x):. The shell method is a method of finding volumes by decomposing a solid of revolution into cylindrical shells. However,. Shell Method Rules.
From math.libretexts.org
3.4b Volumes of Revolution Cylindrical Shells OS Mathematics LibreTexts Shell Method Rules Find an expression that represents the area of a random shell of the can (in terms of x):. Calculate the volume of a solid of revolution by using the method of cylindrical shells. However, we provide a general guideline. There are many different scenarios in which the shell method can be employed, which are not discussed here; Let r be. Shell Method Rules.
From www.slideserve.com
PPT Volumes of Revolution The Shell Method PowerPoint Presentation Shell Method Rules However, we provide a general guideline. This section develops another method of computing volume, the shell method. Consider a region in the plane that is divided into thin vertical strips. Calculate the volume of a solid of revolution by using the method of cylindrical shells. There are many different scenarios in which the shell method can be employed, which are. Shell Method Rules.
From calcworkshop.com
How To Use The Shell Method? (w/ 3 Powerful Examples!) Shell Method Rules Here’s how you use the shell method, step by step, to find the volume of the can: There are many different scenarios in which the shell method can be employed, which are not discussed here; Let r be the region under the curve y = f (x) between x = a and x = b (0 ≤ a <b) (figure. Shell Method Rules.
From www.youtube.com
Calculus 2 Shell Method YouTube Shell Method Rules Instead of slicing the solid perpendicular to the. Here’s how you use the shell method, step by step, to find the volume of the can: Let r be the region under the curve y = f (x) between x = a and x = b (0 ≤ a <b) (figure 1. There are many different scenarios in which the shell. Shell Method Rules.
From www.slideserve.com
PPT June 21, ‘99 PowerPoint Presentation, free download ID6155408 Shell Method Rules Compare the different methods for calculating a volume of revolution. Instead of slicing the solid perpendicular to the. The shell method is a method of finding volumes by decomposing a solid of revolution into cylindrical shells. However, we provide a general guideline. This section develops another method of computing volume, the shell method. Here’s how you use the shell method,. Shell Method Rules.
From calcworkshop.com
How to use the Shell Method? (3 Powerful Examples!) Shell Method Rules Compare the different methods for calculating a volume of revolution. This section develops another method of computing volume, the shell method. The shell method is a method of finding volumes by decomposing a solid of revolution into cylindrical shells. Calculate the volume of a solid of revolution by using the method of cylindrical shells. There are many different scenarios in. Shell Method Rules.
From www.pinterest.com
Shell Method Calculus, Method, Lesson Shell Method Rules However, we provide a general guideline. Calculate the volume of a solid of revolution by using the method of cylindrical shells. 9.4 volumes of solids of revolution: Let r be the region under the curve y = f (x) between x = a and x = b (0 ≤ a <b) (figure 1. This section develops another method of computing. Shell Method Rules.
From www.youtube.com
Shell Method Volume of Revolution YouTube Shell Method Rules There are many different scenarios in which the shell method can be employed, which are not discussed here; Consider a region in the plane that is divided into thin vertical strips. Compare the different methods for calculating a volume of revolution. This section develops another method of computing volume, the shell method. However, we provide a general guideline. Let r. Shell Method Rules.
From www.youtube.com
Shell Method Calculus (Example 1) YouTube Shell Method Rules Consider a region in the plane that is divided into thin vertical strips. Instead of slicing the solid perpendicular to the. The shell method is a method of finding volumes by decomposing a solid of revolution into cylindrical shells. However, we provide a general guideline. Let r be the region under the curve y = f (x) between x =. Shell Method Rules.
From www.youtube.com
Calculus Shell Method YouTube Shell Method Rules Let r be the region under the curve y = f (x) between x = a and x = b (0 ≤ a <b) (figure 1. There are many different scenarios in which the shell method can be employed, which are not discussed here; 9.4 volumes of solids of revolution: However, we provide a general guideline. Compare the different methods. Shell Method Rules.
From www.youtube.com
The Shell Method Examples Calculus 2 JK Math YouTube Shell Method Rules The shell method is a method of finding volumes by decomposing a solid of revolution into cylindrical shells. There are many different scenarios in which the shell method can be employed, which are not discussed here; Here’s how you use the shell method, step by step, to find the volume of the can: Calculate the volume of a solid of. Shell Method Rules.
From www.pinterest.com.mx
How to use the Shell Method? (3 Powerful Examples!) Ap calculus, Ap Shell Method Rules However, we provide a general guideline. Compare the different methods for calculating a volume of revolution. Let r be the region under the curve y = f (x) between x = a and x = b (0 ≤ a <b) (figure 1. Consider a region in the plane that is divided into thin vertical strips. Calculate the volume of a. Shell Method Rules.
From www.youtube.com
Examples of the Shell Method YouTube Shell Method Rules Instead of slicing the solid perpendicular to the. However, we provide a general guideline. Find an expression that represents the area of a random shell of the can (in terms of x):. 9.4 volumes of solids of revolution: Compare the different methods for calculating a volume of revolution. There are many different scenarios in which the shell method can be. Shell Method Rules.
From www.youtube.com
Volume by the Shell Method Problem 2 (Calculus 2) YouTube Shell Method Rules Calculate the volume of a solid of revolution by using the method of cylindrical shells. Instead of slicing the solid perpendicular to the. Find an expression that represents the area of a random shell of the can (in terms of x):. Let r be the region under the curve y = f (x) between x = a and x =. Shell Method Rules.
From www.youtube.com
Calculus 2 Volume (Cylindrical Shell Method) Stewart Chapter 7.1 62 Shell Method Rules Instead of slicing the solid perpendicular to the. Compare the different methods for calculating a volume of revolution. Find an expression that represents the area of a random shell of the can (in terms of x):. Let r be the region under the curve y = f (x) between x = a and x = b (0 ≤ a <b). Shell Method Rules.
From www.slideserve.com
PPT Volume The Shell Method PowerPoint Presentation, free download Shell Method Rules Instead of slicing the solid perpendicular to the. Compare the different methods for calculating a volume of revolution. However, we provide a general guideline. Here’s how you use the shell method, step by step, to find the volume of the can: Find an expression that represents the area of a random shell of the can (in terms of x):. There. Shell Method Rules.
From www.slideserve.com
PPT Aim How do we find volume using the Shell Method? PowerPoint Shell Method Rules This section develops another method of computing volume, the shell method. Find an expression that represents the area of a random shell of the can (in terms of x):. Instead of slicing the solid perpendicular to the. There are many different scenarios in which the shell method can be employed, which are not discussed here; However, we provide a general. Shell Method Rules.
From www.youtube.com
Calculus Shell Method Ex. 3 YouTube Shell Method Rules Find an expression that represents the area of a random shell of the can (in terms of x):. Let r be the region under the curve y = f (x) between x = a and x = b (0 ≤ a <b) (figure 1. Instead of slicing the solid perpendicular to the. This section develops another method of computing volume,. Shell Method Rules.
From calcworkshop.com
How To Use The Shell Method? (w/ 3 Powerful Examples!) Shell Method Rules The shell method is a method of finding volumes by decomposing a solid of revolution into cylindrical shells. Let r be the region under the curve y = f (x) between x = a and x = b (0 ≤ a <b) (figure 1. Find an expression that represents the area of a random shell of the can (in terms. Shell Method Rules.
From www.youtube.com
Calculus 2, Session 11 Volumes by Shell Method YouTube Shell Method Rules Instead of slicing the solid perpendicular to the. Here’s how you use the shell method, step by step, to find the volume of the can: Compare the different methods for calculating a volume of revolution. Let r be the region under the curve y = f (x) between x = a and x = b (0 ≤ a <b) (figure. Shell Method Rules.
From calcworkshop.com
How To Use The Shell Method? (w/ 3 Powerful Examples!) Shell Method Rules Consider a region in the plane that is divided into thin vertical strips. 9.4 volumes of solids of revolution: Let r be the region under the curve y = f (x) between x = a and x = b (0 ≤ a <b) (figure 1. There are many different scenarios in which the shell method can be employed, which are. Shell Method Rules.
From www.slideserve.com
PPT 6.3 Volumes by Cylindrical Shells PowerPoint Presentation, free Shell Method Rules This section develops another method of computing volume, the shell method. Here’s how you use the shell method, step by step, to find the volume of the can: The shell method is a method of finding volumes by decomposing a solid of revolution into cylindrical shells. Compare the different methods for calculating a volume of revolution. 9.4 volumes of solids. Shell Method Rules.
From www.slideserve.com
PPT Volumes of Revolution The Shell Method PowerPoint Presentation Shell Method Rules There are many different scenarios in which the shell method can be employed, which are not discussed here; Here’s how you use the shell method, step by step, to find the volume of the can: This section develops another method of computing volume, the shell method. Instead of slicing the solid perpendicular to the. Compare the different methods for calculating. Shell Method Rules.
From www.youtube.com
Part 2 of shell method with 2 functions of y AP Calculus AB Khan Shell Method Rules Let r be the region under the curve y = f (x) between x = a and x = b (0 ≤ a <b) (figure 1. Consider a region in the plane that is divided into thin vertical strips. This section develops another method of computing volume, the shell method. The shell method is a method of finding volumes by. Shell Method Rules.
From www.slideserve.com
PPT Aim How do we find volume using the Shell Method? PowerPoint Shell Method Rules Let r be the region under the curve y = f (x) between x = a and x = b (0 ≤ a <b) (figure 1. There are many different scenarios in which the shell method can be employed, which are not discussed here; Here’s how you use the shell method, step by step, to find the volume of the. Shell Method Rules.
From www.youtube.com
Calculus 2 Shell Method Practice Problem YouTube Shell Method Rules The shell method is a method of finding volumes by decomposing a solid of revolution into cylindrical shells. 9.4 volumes of solids of revolution: This section develops another method of computing volume, the shell method. There are many different scenarios in which the shell method can be employed, which are not discussed here; Instead of slicing the solid perpendicular to. Shell Method Rules.
From calcworkshop.com
How To Use The Shell Method? (w/ 3 Powerful Examples!) Shell Method Rules Compare the different methods for calculating a volume of revolution. Let r be the region under the curve y = f (x) between x = a and x = b (0 ≤ a <b) (figure 1. Calculate the volume of a solid of revolution by using the method of cylindrical shells. Instead of slicing the solid perpendicular to the. Consider. Shell Method Rules.
From www.youtube.com
Volume of Revolution The Shell Method about the yaxis YouTube Shell Method Rules Here’s how you use the shell method, step by step, to find the volume of the can: The shell method is a method of finding volumes by decomposing a solid of revolution into cylindrical shells. There are many different scenarios in which the shell method can be employed, which are not discussed here; 9.4 volumes of solids of revolution: Compare. Shell Method Rules.
From www.slideserve.com
PPT Applications of Integration PowerPoint Presentation, free Shell Method Rules This section develops another method of computing volume, the shell method. Calculate the volume of a solid of revolution by using the method of cylindrical shells. Compare the different methods for calculating a volume of revolution. Find an expression that represents the area of a random shell of the can (in terms of x):. There are many different scenarios in. Shell Method Rules.
From www.youtube.com
Volume of Revolution The Shell Method about the xaxis YouTube Shell Method Rules This section develops another method of computing volume, the shell method. Find an expression that represents the area of a random shell of the can (in terms of x):. Calculate the volume of a solid of revolution by using the method of cylindrical shells. Consider a region in the plane that is divided into thin vertical strips. However, we provide. Shell Method Rules.