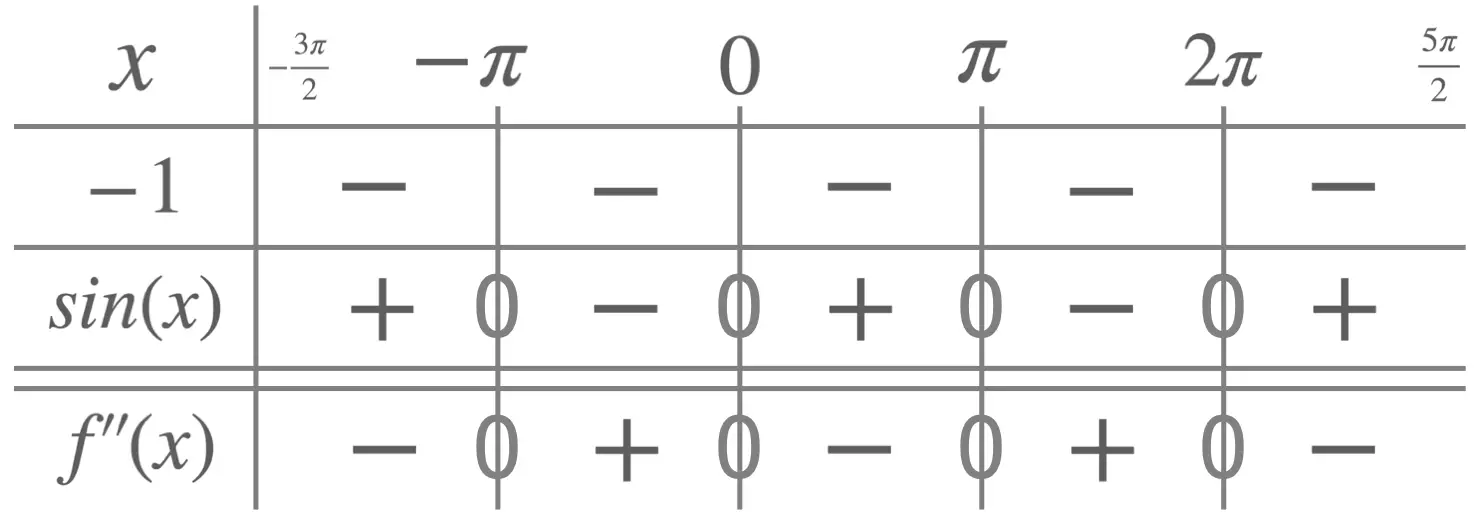
Points Of Inflection Equation at Joshua Mahon blog

Points Of Inflection Equation. the point where the function is neither concave nor convex is known as inflection point or the point of inflection. Inflection points can only occur when the second derivative is zero or undefined. review your knowledge of inflection points and how we use differential calculus to find them. in typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both differentiable at that point\()\) and. the geometric meaning of an inflection point is that the graph of the function f (x) passes from one side of the tangent line to the. an inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or. In this article, the concept and meaning. An inflection point is where a curve changes from concave upward to concave downward (or vice versa) so what is concave upward /.

An inflection point is where a curve changes from concave upward to concave downward (or vice versa) so what is concave upward /. Inflection points can only occur when the second derivative is zero or undefined. the geometric meaning of an inflection point is that the graph of the function f (x) passes from one side of the tangent line to the. in typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both differentiable at that point\()\) and. an inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or. In this article, the concept and meaning. the point where the function is neither concave nor convex is known as inflection point or the point of inflection. review your knowledge of inflection points and how we use differential calculus to find them.

Point of Inflection Calculus

Points Of Inflection Equation an inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or. In this article, the concept and meaning. the point where the function is neither concave nor convex is known as inflection point or the point of inflection. Inflection points can only occur when the second derivative is zero or undefined. review your knowledge of inflection points and how we use differential calculus to find them. An inflection point is where a curve changes from concave upward to concave downward (or vice versa) so what is concave upward /. in typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both differentiable at that point\()\) and. an inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or. the geometric meaning of an inflection point is that the graph of the function f (x) passes from one side of the tangent line to the.