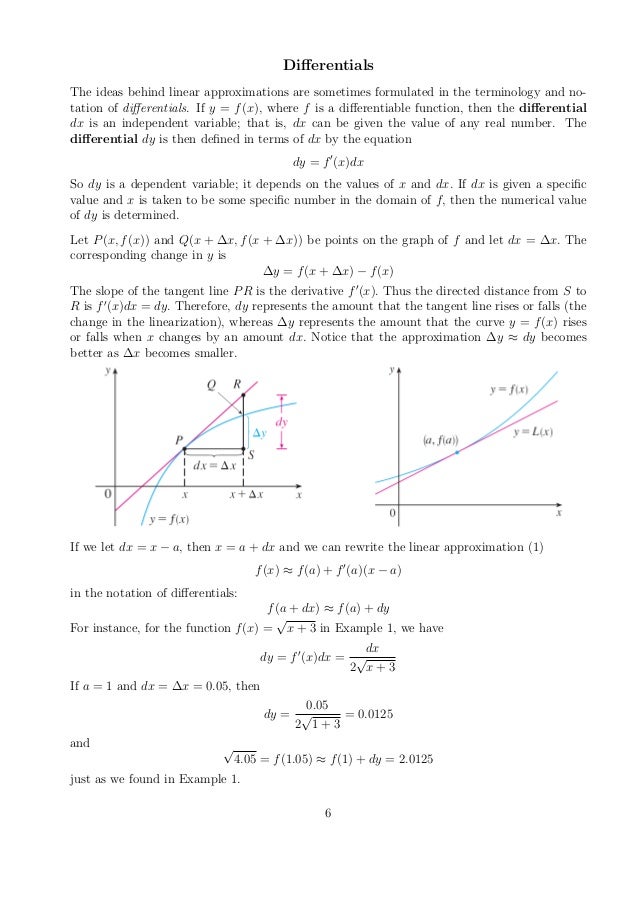
Difference Between Linear Approximation And Differentials . Differentials are useful when the value of a quantity is unimportant, only the approximate change in the quantity in response to a change in input is desired. Linear approximation allows us to estimate the value of f(x +δx) based on the values of f(x) and f ' (x). Write the linearization of a given function. Draw a graph that illustrates the use of differentials to approximate the change in a. Describe the linear approximation to a function at a point. 4.2.2 write the linearization of a given function. Describe the linear approximation to a function at a point. Write the linearization of a given function. As long as the change dx in input x is. A linear approximation is a linear function that approximates something. These very small differences were called differentials, and the subject of derivatives is sometimes called differential calculus,. 4.2.1 describe the linear approximation to a function at a point. A typical formula for a good linear approximation uses. Draw a graph that illustrates the use of differentials to approximate the change in a.
from www.slideshare.net
4.2.1 describe the linear approximation to a function at a point. A linear approximation is a linear function that approximates something. As long as the change dx in input x is. Linear approximation allows us to estimate the value of f(x +δx) based on the values of f(x) and f ' (x). Draw a graph that illustrates the use of differentials to approximate the change in a. Describe the linear approximation to a function at a point. These very small differences were called differentials, and the subject of derivatives is sometimes called differential calculus,. Write the linearization of a given function. Describe the linear approximation to a function at a point. Draw a graph that illustrates the use of differentials to approximate the change in a.
Linear approximations and_differentials
Difference Between Linear Approximation And Differentials A typical formula for a good linear approximation uses. Describe the linear approximation to a function at a point. Draw a graph that illustrates the use of differentials to approximate the change in a. A linear approximation is a linear function that approximates something. Write the linearization of a given function. 4.2.2 write the linearization of a given function. Describe the linear approximation to a function at a point. Differentials are useful when the value of a quantity is unimportant, only the approximate change in the quantity in response to a change in input is desired. Linear approximation allows us to estimate the value of f(x +δx) based on the values of f(x) and f ' (x). As long as the change dx in input x is. 4.2.1 describe the linear approximation to a function at a point. A typical formula for a good linear approximation uses. These very small differences were called differentials, and the subject of derivatives is sometimes called differential calculus,. Draw a graph that illustrates the use of differentials to approximate the change in a. Write the linearization of a given function.
From www.slideserve.com
PPT 3.10 Linear Approximation and Differentials PowerPoint Difference Between Linear Approximation And Differentials Write the linearization of a given function. Describe the linear approximation to a function at a point. A typical formula for a good linear approximation uses. A linear approximation is a linear function that approximates something. These very small differences were called differentials, and the subject of derivatives is sometimes called differential calculus,. Describe the linear approximation to a function. Difference Between Linear Approximation And Differentials.
From www.slideserve.com
PPT Linear Approximation and Differentials PowerPoint Presentation Difference Between Linear Approximation And Differentials Linear approximation allows us to estimate the value of f(x +δx) based on the values of f(x) and f ' (x). Draw a graph that illustrates the use of differentials to approximate the change in a. A linear approximation is a linear function that approximates something. These very small differences were called differentials, and the subject of derivatives is sometimes. Difference Between Linear Approximation And Differentials.
From owlcation.com
Linear Approximation and Differentials in Calculus Owlcation Difference Between Linear Approximation And Differentials Draw a graph that illustrates the use of differentials to approximate the change in a. A typical formula for a good linear approximation uses. 4.2.2 write the linearization of a given function. 4.2.1 describe the linear approximation to a function at a point. Write the linearization of a given function. A linear approximation is a linear function that approximates something.. Difference Between Linear Approximation And Differentials.
From owlcation.com
Linear Approximation and Differentials in Calculus Owlcation Difference Between Linear Approximation And Differentials A typical formula for a good linear approximation uses. Describe the linear approximation to a function at a point. A linear approximation is a linear function that approximates something. Draw a graph that illustrates the use of differentials to approximate the change in a. 4.2.2 write the linearization of a given function. Write the linearization of a given function. As. Difference Between Linear Approximation And Differentials.
From loopspk.com
What is the difference between linear and non linear differential equation Difference Between Linear Approximation And Differentials These very small differences were called differentials, and the subject of derivatives is sometimes called differential calculus,. Describe the linear approximation to a function at a point. Describe the linear approximation to a function at a point. Linear approximation allows us to estimate the value of f(x +δx) based on the values of f(x) and f ' (x). As long. Difference Between Linear Approximation And Differentials.
From www.youtube.com
3.8 Linear Approximation and Differentials YouTube Difference Between Linear Approximation And Differentials Describe the linear approximation to a function at a point. These very small differences were called differentials, and the subject of derivatives is sometimes called differential calculus,. 4.2.1 describe the linear approximation to a function at a point. Describe the linear approximation to a function at a point. Write the linearization of a given function. Write the linearization of a. Difference Between Linear Approximation And Differentials.
From owlcation.com
Linear Approximation and Differentials in Calculus Owlcation Difference Between Linear Approximation And Differentials Draw a graph that illustrates the use of differentials to approximate the change in a. As long as the change dx in input x is. Describe the linear approximation to a function at a point. Linear approximation allows us to estimate the value of f(x +δx) based on the values of f(x) and f ' (x). Describe the linear approximation. Difference Between Linear Approximation And Differentials.
From www.slideserve.com
PPT Section 3.9 Differentials PowerPoint Presentation, free Difference Between Linear Approximation And Differentials These very small differences were called differentials, and the subject of derivatives is sometimes called differential calculus,. Describe the linear approximation to a function at a point. Write the linearization of a given function. Draw a graph that illustrates the use of differentials to approximate the change in a. As long as the change dx in input x is. Draw. Difference Between Linear Approximation And Differentials.
From study.com
Linear Approximations Equation & Examples Lesson Difference Between Linear Approximation And Differentials Write the linearization of a given function. Describe the linear approximation to a function at a point. Describe the linear approximation to a function at a point. A linear approximation is a linear function that approximates something. Differentials are useful when the value of a quantity is unimportant, only the approximate change in the quantity in response to a change. Difference Between Linear Approximation And Differentials.
From www.youtube.com
Total Differentials and Linear Approximations YouTube Difference Between Linear Approximation And Differentials Describe the linear approximation to a function at a point. 4.2.2 write the linearization of a given function. Write the linearization of a given function. Draw a graph that illustrates the use of differentials to approximate the change in a. Describe the linear approximation to a function at a point. As long as the change dx in input x is.. Difference Between Linear Approximation And Differentials.
From www.slideserve.com
PPT Linear Approximation and Differentials PowerPoint Presentation Difference Between Linear Approximation And Differentials A typical formula for a good linear approximation uses. Draw a graph that illustrates the use of differentials to approximate the change in a. 4.2.1 describe the linear approximation to a function at a point. A linear approximation is a linear function that approximates something. Draw a graph that illustrates the use of differentials to approximate the change in a.. Difference Between Linear Approximation And Differentials.
From www.slideserve.com
PPT Linear approximation and differentials ( Section 3.9) PowerPoint Difference Between Linear Approximation And Differentials 4.2.1 describe the linear approximation to a function at a point. A linear approximation is a linear function that approximates something. Differentials are useful when the value of a quantity is unimportant, only the approximate change in the quantity in response to a change in input is desired. Describe the linear approximation to a function at a point. Write the. Difference Between Linear Approximation And Differentials.
From www.youtube.com
Applied Calculus Differentials And Linear Approximations YouTube Difference Between Linear Approximation And Differentials Differentials are useful when the value of a quantity is unimportant, only the approximate change in the quantity in response to a change in input is desired. Linear approximation allows us to estimate the value of f(x +δx) based on the values of f(x) and f ' (x). Write the linearization of a given function. A linear approximation is a. Difference Between Linear Approximation And Differentials.
From www.slideserve.com
PPT Linear Approximation and Differentials PowerPoint Presentation Difference Between Linear Approximation And Differentials 4.2.1 describe the linear approximation to a function at a point. Write the linearization of a given function. A typical formula for a good linear approximation uses. 4.2.2 write the linearization of a given function. Describe the linear approximation to a function at a point. Linear approximation allows us to estimate the value of f(x +δx) based on the values. Difference Between Linear Approximation And Differentials.
From www.slideserve.com
PPT 3.10 Linear Approximation and Differentials PowerPoint Difference Between Linear Approximation And Differentials Describe the linear approximation to a function at a point. As long as the change dx in input x is. A typical formula for a good linear approximation uses. 4.2.2 write the linearization of a given function. Draw a graph that illustrates the use of differentials to approximate the change in a. Describe the linear approximation to a function at. Difference Between Linear Approximation And Differentials.
From owlcation.com
Linear Approximation and Differentials in Calculus Owlcation Difference Between Linear Approximation And Differentials As long as the change dx in input x is. A linear approximation is a linear function that approximates something. Describe the linear approximation to a function at a point. Write the linearization of a given function. Write the linearization of a given function. These very small differences were called differentials, and the subject of derivatives is sometimes called differential. Difference Between Linear Approximation And Differentials.
From www.youtube.com
Local Linear Approximations and Differentials YouTube Difference Between Linear Approximation And Differentials Linear approximation allows us to estimate the value of f(x +δx) based on the values of f(x) and f ' (x). A typical formula for a good linear approximation uses. A linear approximation is a linear function that approximates something. Write the linearization of a given function. Draw a graph that illustrates the use of differentials to approximate the change. Difference Between Linear Approximation And Differentials.
From www.slideshare.net
Lesson 12 Linear Approximation and Differentials (Section 41 slides) Difference Between Linear Approximation And Differentials Linear approximation allows us to estimate the value of f(x +δx) based on the values of f(x) and f ' (x). Describe the linear approximation to a function at a point. A linear approximation is a linear function that approximates something. As long as the change dx in input x is. Write the linearization of a given function. A typical. Difference Between Linear Approximation And Differentials.
From www.youtube.com
DIFFERENTIALS PART 1 LINEAR APPROXIMATIONS YouTube Difference Between Linear Approximation And Differentials 4.2.2 write the linearization of a given function. A typical formula for a good linear approximation uses. These very small differences were called differentials, and the subject of derivatives is sometimes called differential calculus,. Linear approximation allows us to estimate the value of f(x +δx) based on the values of f(x) and f ' (x). 4.2.1 describe the linear approximation. Difference Between Linear Approximation And Differentials.
From www.youtube.com
4.2 Linear Approximations and Differentials YouTube Difference Between Linear Approximation And Differentials These very small differences were called differentials, and the subject of derivatives is sometimes called differential calculus,. Linear approximation allows us to estimate the value of f(x +δx) based on the values of f(x) and f ' (x). Describe the linear approximation to a function at a point. Draw a graph that illustrates the use of differentials to approximate the. Difference Between Linear Approximation And Differentials.
From www.youtube.com
LINEAR APPROXIMATIONS AND DIFFERENTIALS YouTube Difference Between Linear Approximation And Differentials Write the linearization of a given function. These very small differences were called differentials, and the subject of derivatives is sometimes called differential calculus,. Linear approximation allows us to estimate the value of f(x +δx) based on the values of f(x) and f ' (x). As long as the change dx in input x is. A typical formula for a. Difference Between Linear Approximation And Differentials.
From www.slideserve.com
PPT 3.10 Linear Approximation and Differentials PowerPoint Difference Between Linear Approximation And Differentials Draw a graph that illustrates the use of differentials to approximate the change in a. 4.2.1 describe the linear approximation to a function at a point. As long as the change dx in input x is. Describe the linear approximation to a function at a point. A typical formula for a good linear approximation uses. Differentials are useful when the. Difference Between Linear Approximation And Differentials.
From www.slideserve.com
PPT Linear approximation and differentials ( Section 3.9) PowerPoint Difference Between Linear Approximation And Differentials 4.2.2 write the linearization of a given function. These very small differences were called differentials, and the subject of derivatives is sometimes called differential calculus,. Describe the linear approximation to a function at a point. A linear approximation is a linear function that approximates something. 4.2.1 describe the linear approximation to a function at a point. Write the linearization of. Difference Between Linear Approximation And Differentials.
From www.slideserve.com
PPT NUMERICAL DIFFERENTIATION or DIFFERENCE APPROXIMATION PowerPoint Difference Between Linear Approximation And Differentials Write the linearization of a given function. Draw a graph that illustrates the use of differentials to approximate the change in a. Describe the linear approximation to a function at a point. Draw a graph that illustrates the use of differentials to approximate the change in a. As long as the change dx in input x is. These very small. Difference Between Linear Approximation And Differentials.
From www.slideserve.com
PPT 4.5 Linear Approximations, Differentials and Newton’s Method Difference Between Linear Approximation And Differentials Linear approximation allows us to estimate the value of f(x +δx) based on the values of f(x) and f ' (x). Draw a graph that illustrates the use of differentials to approximate the change in a. 4.2.1 describe the linear approximation to a function at a point. These very small differences were called differentials, and the subject of derivatives is. Difference Between Linear Approximation And Differentials.
From www.slideserve.com
PPT Calculus Notes 3.9 & 3.10 Related Rates & Linear Approximations Difference Between Linear Approximation And Differentials Differentials are useful when the value of a quantity is unimportant, only the approximate change in the quantity in response to a change in input is desired. These very small differences were called differentials, and the subject of derivatives is sometimes called differential calculus,. Describe the linear approximation to a function at a point. Write the linearization of a given. Difference Between Linear Approximation And Differentials.
From www.slideserve.com
PPT 3.10 Linear Approximation and Differentials PowerPoint Difference Between Linear Approximation And Differentials Draw a graph that illustrates the use of differentials to approximate the change in a. 4.2.2 write the linearization of a given function. A linear approximation is a linear function that approximates something. Write the linearization of a given function. Draw a graph that illustrates the use of differentials to approximate the change in a. As long as the change. Difference Between Linear Approximation And Differentials.
From www.youtube.com
Calculus I Linear approximations and differentials YouTube Difference Between Linear Approximation And Differentials These very small differences were called differentials, and the subject of derivatives is sometimes called differential calculus,. Write the linearization of a given function. 4.2.1 describe the linear approximation to a function at a point. Write the linearization of a given function. Draw a graph that illustrates the use of differentials to approximate the change in a. As long as. Difference Between Linear Approximation And Differentials.
From www.youtube.com
Linear Approximations and Differentials YouTube Difference Between Linear Approximation And Differentials Write the linearization of a given function. Draw a graph that illustrates the use of differentials to approximate the change in a. Describe the linear approximation to a function at a point. As long as the change dx in input x is. Differentials are useful when the value of a quantity is unimportant, only the approximate change in the quantity. Difference Between Linear Approximation And Differentials.
From www.slideshare.net
Linear approximations and_differentials Difference Between Linear Approximation And Differentials A typical formula for a good linear approximation uses. A linear approximation is a linear function that approximates something. These very small differences were called differentials, and the subject of derivatives is sometimes called differential calculus,. Draw a graph that illustrates the use of differentials to approximate the change in a. Draw a graph that illustrates the use of differentials. Difference Between Linear Approximation And Differentials.
From owlcation.com
Linear Approximation and Differentials in Calculus Owlcation Difference Between Linear Approximation And Differentials Draw a graph that illustrates the use of differentials to approximate the change in a. Describe the linear approximation to a function at a point. 4.2.2 write the linearization of a given function. Linear approximation allows us to estimate the value of f(x +δx) based on the values of f(x) and f ' (x). Draw a graph that illustrates the. Difference Between Linear Approximation And Differentials.
From www.slideshare.net
Lesson 12 Linear Approximation and Differentials (Section 41 slides) Difference Between Linear Approximation And Differentials Draw a graph that illustrates the use of differentials to approximate the change in a. As long as the change dx in input x is. Linear approximation allows us to estimate the value of f(x +δx) based on the values of f(x) and f ' (x). These very small differences were called differentials, and the subject of derivatives is sometimes. Difference Between Linear Approximation And Differentials.
From owlcation.com
Linear Approximation and Differentials in Calculus Owlcation Difference Between Linear Approximation And Differentials Linear approximation allows us to estimate the value of f(x +δx) based on the values of f(x) and f ' (x). Draw a graph that illustrates the use of differentials to approximate the change in a. Describe the linear approximation to a function at a point. A typical formula for a good linear approximation uses. As long as the change. Difference Between Linear Approximation And Differentials.
From www.youtube.com
3.6 Local Linear Approximations; Differentials YouTube Difference Between Linear Approximation And Differentials Describe the linear approximation to a function at a point. These very small differences were called differentials, and the subject of derivatives is sometimes called differential calculus,. Write the linearization of a given function. Write the linearization of a given function. 4.2.2 write the linearization of a given function. Draw a graph that illustrates the use of differentials to approximate. Difference Between Linear Approximation And Differentials.
From slideplayer.com
§3.10 Linear Approximations and Differentials ppt download Difference Between Linear Approximation And Differentials Describe the linear approximation to a function at a point. 4.2.1 describe the linear approximation to a function at a point. 4.2.2 write the linearization of a given function. A typical formula for a good linear approximation uses. Write the linearization of a given function. Draw a graph that illustrates the use of differentials to approximate the change in a.. Difference Between Linear Approximation And Differentials.