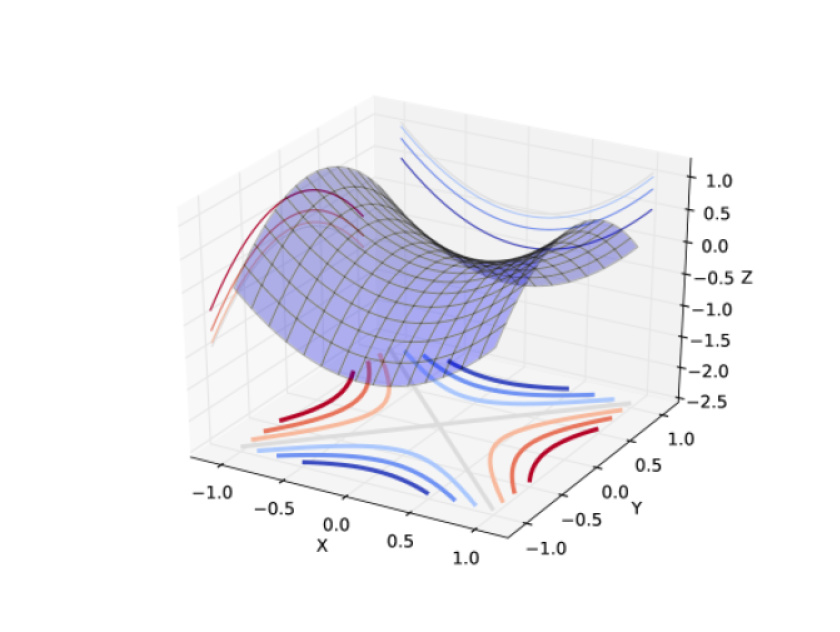
Saddle Point Definition . A saddle point is a critical point on a surface where the slopes in perpendicular directions differ; The saddle point in the context of a function of the two or more variables is a point on the graph where the function does not exhibit a. A saddle point is a critical point on a potential energy surface where the potential energy is neither at a local maximum nor a local minimum, resembling. Saddle points are critical points of a multivariable function where the function has neither a local maximum nor a local minimum. One slope is positive while the other is negative. A saddle point, also known as a minimax point, is a concept primarily used in game theory and optimization. A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a. A saddle point is a point on a curved surface where the curvatures in two perpendicular planes are opposite, or a value of a function where it has both.
from deepai.org
A saddle point is a critical point on a surface where the slopes in perpendicular directions differ; A saddle point, also known as a minimax point, is a concept primarily used in game theory and optimization. Saddle points are critical points of a multivariable function where the function has neither a local maximum nor a local minimum. A saddle point is a point on a curved surface where the curvatures in two perpendicular planes are opposite, or a value of a function where it has both. A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a. The saddle point in the context of a function of the two or more variables is a point on the graph where the function does not exhibit a. One slope is positive while the other is negative. A saddle point is a critical point on a potential energy surface where the potential energy is neither at a local maximum nor a local minimum, resembling.
On the saddle point problem for nonconvex optimization DeepAI
Saddle Point Definition A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a. The saddle point in the context of a function of the two or more variables is a point on the graph where the function does not exhibit a. A saddle point is a critical point on a surface where the slopes in perpendicular directions differ; One slope is positive while the other is negative. A saddle point is a point on a curved surface where the curvatures in two perpendicular planes are opposite, or a value of a function where it has both. A saddle point is a critical point on a potential energy surface where the potential energy is neither at a local maximum nor a local minimum, resembling. Saddle points are critical points of a multivariable function where the function has neither a local maximum nor a local minimum. A saddle point, also known as a minimax point, is a concept primarily used in game theory and optimization. A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a.
From erickimphotography.com
Hyperbolic Geometry Saddle Point Definition The saddle point in the context of a function of the two or more variables is a point on the graph where the function does not exhibit a. One slope is positive while the other is negative. A saddle point is a critical point on a potential energy surface where the potential energy is neither at a local maximum nor. Saddle Point Definition.
From www.researchgate.net
The minima, saddle points, and inflection points are displayed as an Saddle Point Definition A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a. A saddle point is a point on a curved surface where the curvatures in two perpendicular planes are opposite, or a value of a function where it has both. A saddle point is a critical point on a potential energy surface where the. Saddle Point Definition.
From deepai.org
On the saddle point problem for nonconvex optimization DeepAI Saddle Point Definition A saddle point is a point on a curved surface where the curvatures in two perpendicular planes are opposite, or a value of a function where it has both. A saddle point, also known as a minimax point, is a concept primarily used in game theory and optimization. A saddle point is a critical point on a surface where the. Saddle Point Definition.
From mathinsight.org
Introduction to local extrema of functions of two variables Math Insight Saddle Point Definition A saddle point is a point on a curved surface where the curvatures in two perpendicular planes are opposite, or a value of a function where it has both. One slope is positive while the other is negative. A saddle point is a critical point on a potential energy surface where the potential energy is neither at a local maximum. Saddle Point Definition.
From www.researchgate.net
The saddle point in the displacement versus time graph Download Saddle Point Definition A saddle point is a critical point on a surface where the slopes in perpendicular directions differ; One slope is positive while the other is negative. The saddle point in the context of a function of the two or more variables is a point on the graph where the function does not exhibit a. A saddle point is a critical. Saddle Point Definition.
From www.youtube.com
Saddle point YouTube Saddle Point Definition A saddle point is a critical point on a surface where the slopes in perpendicular directions differ; A saddle point, also known as a minimax point, is a concept primarily used in game theory and optimization. Saddle points are critical points of a multivariable function where the function has neither a local maximum nor a local minimum. A saddle point. Saddle Point Definition.
From medium.com
Recipe secret for machine learning optimization by Marianne Arrué Saddle Point Definition A saddle point is a point on a curved surface where the curvatures in two perpendicular planes are opposite, or a value of a function where it has both. A saddle point, also known as a minimax point, is a concept primarily used in game theory and optimization. A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is. Saddle Point Definition.
From users.dimi.uniud.it
Mathematica notebooks Saddle Point Definition The saddle point in the context of a function of the two or more variables is a point on the graph where the function does not exhibit a. Saddle points are critical points of a multivariable function where the function has neither a local maximum nor a local minimum. A saddle point is a critical point on a potential energy. Saddle Point Definition.
From www.youtube.com
saddle point in game theory Optimal strategy value of game Saddle Point Definition A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a. Saddle points are critical points of a multivariable function where the function has neither a local maximum nor a local minimum. A saddle point is a point on a curved surface where the curvatures in two perpendicular planes are opposite, or a value. Saddle Point Definition.
From www.youtube.com
Three Dimensional Linear Saddle Point Example, Invariant Subspaces and Saddle Point Definition A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a. A saddle point, also known as a minimax point, is a concept primarily used in game theory and optimization. A saddle point is a point on a curved surface where the curvatures in two perpendicular planes are opposite, or a value of a. Saddle Point Definition.
From m-alcu.github.io
Cycling learning rate Saddle Point Definition The saddle point in the context of a function of the two or more variables is a point on the graph where the function does not exhibit a. A saddle point, also known as a minimax point, is a concept primarily used in game theory and optimization. A saddle point is a critical point on a potential energy surface where. Saddle Point Definition.
From www.researchgate.net
Schematic picture of the concept of perturbing the saddle point P in Saddle Point Definition Saddle points are critical points of a multivariable function where the function has neither a local maximum nor a local minimum. A saddle point, also known as a minimax point, is a concept primarily used in game theory and optimization. One slope is positive while the other is negative. A saddle point is a critical point on a surface where. Saddle Point Definition.
From www.slideserve.com
PPT Ch121a Atomic Level Simulations of Materials and Molecules Saddle Point Definition A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a. One slope is positive while the other is negative. The saddle point in the context of a function of the two or more variables is a point on the graph where the function does not exhibit a. A saddle point, also known as. Saddle Point Definition.
From www.youtube.com
Calc III Lesson 18 Relative Extrema and Saddle Points.mp4 YouTube Saddle Point Definition A saddle point, also known as a minimax point, is a concept primarily used in game theory and optimization. A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a. One slope is positive while the other is negative. The saddle point in the context of a function of the two or more variables. Saddle Point Definition.
From bookdown.org
Chapter 9 Stationary Points MATH1006 Calculus Saddle Point Definition A saddle point is a point on a curved surface where the curvatures in two perpendicular planes are opposite, or a value of a function where it has both. A saddle point, also known as a minimax point, is a concept primarily used in game theory and optimization. The saddle point in the context of a function of the two. Saddle Point Definition.
From www.slideserve.com
PPT Short Version 12. Static Equilibrium PowerPoint Presentation Saddle Point Definition A saddle point is a critical point on a surface where the slopes in perpendicular directions differ; Saddle points are critical points of a multivariable function where the function has neither a local maximum nor a local minimum. One slope is positive while the other is negative. A saddle point is a critical point on a potential energy surface where. Saddle Point Definition.
From www.youtube.com
Unit 222 Saddle Points YouTube Saddle Point Definition A saddle point is a critical point on a potential energy surface where the potential energy is neither at a local maximum nor a local minimum, resembling. A saddle point, also known as a minimax point, is a concept primarily used in game theory and optimization. A saddle point is a critical point on a surface where the slopes in. Saddle Point Definition.
From www.coursehero.com
[Solved] . Find the local maximum and minimum values and saddle point(s Saddle Point Definition Saddle points are critical points of a multivariable function where the function has neither a local maximum nor a local minimum. One slope is positive while the other is negative. A saddle point is a point on a curved surface where the curvatures in two perpendicular planes are opposite, or a value of a function where it has both. A. Saddle Point Definition.
From www.slideserve.com
PPT Applied Economics for Business Management PowerPoint Presentation Saddle Point Definition A saddle point is a point on a curved surface where the curvatures in two perpendicular planes are opposite, or a value of a function where it has both. One slope is positive while the other is negative. A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a. Saddle points are critical points. Saddle Point Definition.
From www.slideserve.com
PPT Game Theory and Strategy PowerPoint Presentation, free download Saddle Point Definition The saddle point in the context of a function of the two or more variables is a point on the graph where the function does not exhibit a. Saddle points are critical points of a multivariable function where the function has neither a local maximum nor a local minimum. A saddle point is a critical point on a surface where. Saddle Point Definition.
From www.youtube.com
Critical Points Saddle Points Stationary Point and Point of Inflection Saddle Point Definition A saddle point is a critical point on a potential energy surface where the potential energy is neither at a local maximum nor a local minimum, resembling. A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a. Saddle points are critical points of a multivariable function where the function has neither a local. Saddle Point Definition.
From yosefnewsrogers.blogspot.com
Find Critical Points of Multivariable Function Calculator Saddle Point Definition A saddle point is a critical point on a surface where the slopes in perpendicular directions differ; A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a. A saddle point, also known as a minimax point, is a concept primarily used in game theory and optimization. A saddle point is a point on. Saddle Point Definition.
From mathsathome.com
How to Find and Classify Stationary Points Saddle Point Definition A saddle point is a point on a curved surface where the curvatures in two perpendicular planes are opposite, or a value of a function where it has both. One slope is positive while the other is negative. A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a. The saddle point in the. Saddle Point Definition.
From dl-uk.apowersoft.com
Ati 3 Critical Points Template Saddle Point Definition A saddle point is a critical point on a surface where the slopes in perpendicular directions differ; A saddle point, also known as a minimax point, is a concept primarily used in game theory and optimization. A saddle point is a critical point on a potential energy surface where the potential energy is neither at a local maximum nor a. Saddle Point Definition.
From www.youtube.com
14 Minima, maxima and saddles points YouTube Saddle Point Definition A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a. One slope is positive while the other is negative. A saddle point is a critical point on a surface where the slopes in perpendicular directions differ; A saddle point is a critical point on a potential energy surface where the potential energy is. Saddle Point Definition.
From www.researchgate.net
Saddle point in deep neural network Download Scientific Diagram Saddle Point Definition A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a. A saddle point, also known as a minimax point, is a concept primarily used in game theory and optimization. A saddle point is a critical point on a surface where the slopes in perpendicular directions differ; A saddle point is a point on. Saddle Point Definition.
From bair.berkeley.edu
How to Escape Saddle Points Efficiently The Berkeley Artificial Saddle Point Definition The saddle point in the context of a function of the two or more variables is a point on the graph where the function does not exhibit a. A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a. A saddle point is a critical point on a surface where the slopes in perpendicular. Saddle Point Definition.
From spie.org
Saddle points reveal essential properties of the meritfunction landscape Saddle Point Definition A saddle point is a critical point on a potential energy surface where the potential energy is neither at a local maximum nor a local minimum, resembling. A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a. A saddle point is a point on a curved surface where the curvatures in two perpendicular. Saddle Point Definition.
From www.slideserve.com
PPT PARTIAL DERIVATIVES PowerPoint Presentation, free download ID Saddle Point Definition A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a. Saddle points are critical points of a multivariable function where the function has neither a local maximum nor a local minimum. A saddle point is a critical point on a potential energy surface where the potential energy is neither at a local maximum. Saddle Point Definition.
From www.jeremyjordan.me
Setting the learning rate of your neural network. Saddle Point Definition A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a. Saddle points are critical points of a multivariable function where the function has neither a local maximum nor a local minimum. The saddle point in the context of a function of the two or more variables is a point on the graph where. Saddle Point Definition.
From bookdown.org
Chapter 9 Stationary Points MATH1006 Calculus Saddle Point Definition A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a. A saddle point is a critical point on a surface where the slopes in perpendicular directions differ; The saddle point in the context of a function of the two or more variables is a point on the graph where the function does not. Saddle Point Definition.
From calcworkshop.com
Saddle Point (How To Find 'Em w/ StepbyStep Examples!) Saddle Point Definition A saddle point is a critical point on a surface where the slopes in perpendicular directions differ; A saddle point is a point on a curved surface where the curvatures in two perpendicular planes are opposite, or a value of a function where it has both. One slope is positive while the other is negative. A saddle point is a. Saddle Point Definition.
From calcworkshop.com
Saddle Point (How To Find 'Em w/ StepbyStep Examples!) Saddle Point Definition Saddle points are critical points of a multivariable function where the function has neither a local maximum nor a local minimum. A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a. A saddle point is a critical point on a potential energy surface where the potential energy is neither at a local maximum. Saddle Point Definition.
From www.youtube.com
Differences Between Stationary Point Saddle Point and Point of Saddle Point Definition A saddle point, also known as a minimax point, is a concept primarily used in game theory and optimization. One slope is positive while the other is negative. A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a. A saddle point is a point on a curved surface where the curvatures in two. Saddle Point Definition.
From wiki.rankiing.net
Is saddle point stable? Rankiing Wiki Facts, Films, Séries, Animes Saddle Point Definition A saddle point is a point on a curved surface where the curvatures in two perpendicular planes are opposite, or a value of a function where it has both. A saddle point, also known as a minimax point, is a concept primarily used in game theory and optimization. A saddle point is a critical point on a surface where the. Saddle Point Definition.