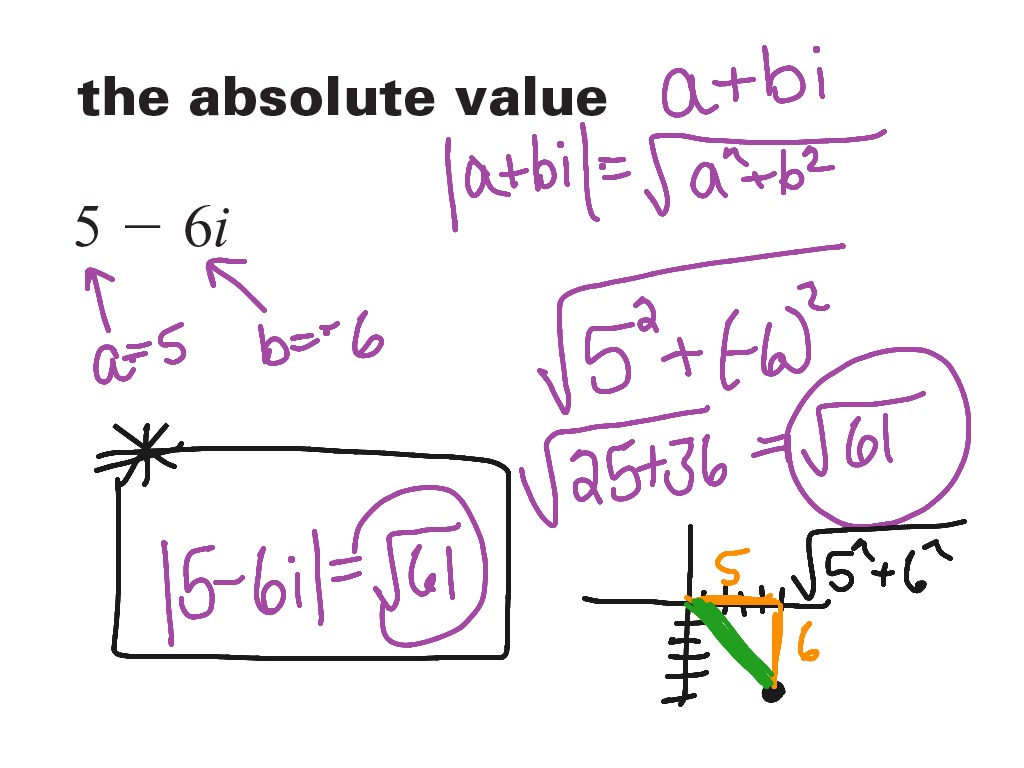
Absolute Value With Imaginary Numbers . Absolute value of complex numbers explained with diagrams, examples several practice problems. The absolute value of a complex number, a + bi (also called the modulus) is defined as the distance between the origin (0, 0) and the point (a, b) in the complex plane. Prove algebraic properties of addition and multiplication of complex numbers, and apply these properties. For a complex number in polar form r (cos θ + i sin θ). Understand the action of taking the conjugate of a. This is because all of them are one unit away from 0, either on. The absolute value of a + bi is written | a + bi |, and the formula for | a + bi | is √a2+b2 a 2 + b 2. Complex numbers can have an absolute value of 1.
from www.showme.com
This is because all of them are one unit away from 0, either on. The absolute value of a complex number, a + bi (also called the modulus) is defined as the distance between the origin (0, 0) and the point (a, b) in the complex plane. Prove algebraic properties of addition and multiplication of complex numbers, and apply these properties. The absolute value of a + bi is written | a + bi |, and the formula for | a + bi | is √a2+b2 a 2 + b 2. For a complex number in polar form r (cos θ + i sin θ). Understand the action of taking the conjugate of a. Complex numbers can have an absolute value of 1. Absolute value of complex numbers explained with diagrams, examples several practice problems.
Absolute Value of Complex Number Math, Algebra, Algebra 2, Complex
Absolute Value With Imaginary Numbers Absolute value of complex numbers explained with diagrams, examples several practice problems. For a complex number in polar form r (cos θ + i sin θ). Complex numbers can have an absolute value of 1. Prove algebraic properties of addition and multiplication of complex numbers, and apply these properties. Absolute value of complex numbers explained with diagrams, examples several practice problems. The absolute value of a + bi is written | a + bi |, and the formula for | a + bi | is √a2+b2 a 2 + b 2. This is because all of them are one unit away from 0, either on. Understand the action of taking the conjugate of a. The absolute value of a complex number, a + bi (also called the modulus) is defined as the distance between the origin (0, 0) and the point (a, b) in the complex plane.
From www.youtube.com
Absolute Value Of Complex Numbers Absolute Value Absolute Value Of Absolute Value With Imaginary Numbers The absolute value of a complex number, a + bi (also called the modulus) is defined as the distance between the origin (0, 0) and the point (a, b) in the complex plane. This is because all of them are one unit away from 0, either on. Complex numbers can have an absolute value of 1. The absolute value of. Absolute Value With Imaginary Numbers.
From datascienceparichay.com
Python Get the Absolute Value of a Complex Number Data Science Parichay Absolute Value With Imaginary Numbers Prove algebraic properties of addition and multiplication of complex numbers, and apply these properties. Absolute value of complex numbers explained with diagrams, examples several practice problems. Understand the action of taking the conjugate of a. The absolute value of a complex number, a + bi (also called the modulus) is defined as the distance between the origin (0, 0) and. Absolute Value With Imaginary Numbers.
From www.codingem.com
Python Absolute Value 'abs()' — A Complete Guide (with Examples) Absolute Value With Imaginary Numbers The absolute value of a complex number, a + bi (also called the modulus) is defined as the distance between the origin (0, 0) and the point (a, b) in the complex plane. For a complex number in polar form r (cos θ + i sin θ). The absolute value of a + bi is written | a + bi. Absolute Value With Imaginary Numbers.
From apluscalculus.com
Finding Absolute Value of a Complex Number 4 Key Steps Absolute Value With Imaginary Numbers Complex numbers can have an absolute value of 1. Prove algebraic properties of addition and multiplication of complex numbers, and apply these properties. For a complex number in polar form r (cos θ + i sin θ). This is because all of them are one unit away from 0, either on. Understand the action of taking the conjugate of a.. Absolute Value With Imaginary Numbers.
From funrithmetic.com
Absolute Value of Complex Numbers Zen Math Funrithmetic Absolute Value With Imaginary Numbers The absolute value of a complex number, a + bi (also called the modulus) is defined as the distance between the origin (0, 0) and the point (a, b) in the complex plane. This is because all of them are one unit away from 0, either on. For a complex number in polar form r (cos θ + i sin. Absolute Value With Imaginary Numbers.
From www.youtube.com
PreCal Absolute Value & Conjugate of Complex Numbers (Solved by Hand Absolute Value With Imaginary Numbers This is because all of them are one unit away from 0, either on. Understand the action of taking the conjugate of a. For a complex number in polar form r (cos θ + i sin θ). Prove algebraic properties of addition and multiplication of complex numbers, and apply these properties. The absolute value of a + bi is written. Absolute Value With Imaginary Numbers.
From askworksheet.com
Absolute Value Worksheets With Number Lines Askworksheet Absolute Value With Imaginary Numbers Understand the action of taking the conjugate of a. Prove algebraic properties of addition and multiplication of complex numbers, and apply these properties. For a complex number in polar form r (cos θ + i sin θ). The absolute value of a + bi is written | a + bi |, and the formula for | a + bi |. Absolute Value With Imaginary Numbers.
From www.youtube.com
Learn how to find the absolute value of complex numbers explained easy Absolute Value With Imaginary Numbers Complex numbers can have an absolute value of 1. For a complex number in polar form r (cos θ + i sin θ). The absolute value of a + bi is written | a + bi |, and the formula for | a + bi | is √a2+b2 a 2 + b 2. The absolute value of a complex number,. Absolute Value With Imaginary Numbers.
From www.youtube.com
Absolute Value of Complex Numbers YouTube Absolute Value With Imaginary Numbers Understand the action of taking the conjugate of a. The absolute value of a + bi is written | a + bi |, and the formula for | a + bi | is √a2+b2 a 2 + b 2. Absolute value of complex numbers explained with diagrams, examples several practice problems. The absolute value of a complex number, a +. Absolute Value With Imaginary Numbers.
From mathsux.org
Absolute Value Equations Algebra Math Lessons Absolute Value With Imaginary Numbers The absolute value of a + bi is written | a + bi |, and the formula for | a + bi | is √a2+b2 a 2 + b 2. For a complex number in polar form r (cos θ + i sin θ). Absolute value of complex numbers explained with diagrams, examples several practice problems. Prove algebraic properties of. Absolute Value With Imaginary Numbers.
From jillwilliams.github.io
Absolute Value of Complex Numbers Absolute Value With Imaginary Numbers The absolute value of a + bi is written | a + bi |, and the formula for | a + bi | is √a2+b2 a 2 + b 2. Absolute value of complex numbers explained with diagrams, examples several practice problems. Complex numbers can have an absolute value of 1. The absolute value of a complex number, a +. Absolute Value With Imaginary Numbers.
From www.showme.com
Absolute value of a complex number Math, Algebra 2 ShowMe Absolute Value With Imaginary Numbers The absolute value of a complex number, a + bi (also called the modulus) is defined as the distance between the origin (0, 0) and the point (a, b) in the complex plane. Understand the action of taking the conjugate of a. Absolute value of complex numbers explained with diagrams, examples several practice problems. The absolute value of a +. Absolute Value With Imaginary Numbers.
From www.showme.com
Absolute value of complex numbers Math, Algebra, Quadratic Formula Absolute Value With Imaginary Numbers Absolute value of complex numbers explained with diagrams, examples several practice problems. The absolute value of a complex number, a + bi (also called the modulus) is defined as the distance between the origin (0, 0) and the point (a, b) in the complex plane. Complex numbers can have an absolute value of 1. For a complex number in polar. Absolute Value With Imaginary Numbers.
From worksheetzone.org
Complex Numbers And Absolute Value Worksheet Absolute Value With Imaginary Numbers The absolute value of a complex number, a + bi (also called the modulus) is defined as the distance between the origin (0, 0) and the point (a, b) in the complex plane. Understand the action of taking the conjugate of a. This is because all of them are one unit away from 0, either on. For a complex number. Absolute Value With Imaginary Numbers.
From jillwilliams.github.io
Absolute Value of Complex Numbers Absolute Value With Imaginary Numbers Complex numbers can have an absolute value of 1. This is because all of them are one unit away from 0, either on. Prove algebraic properties of addition and multiplication of complex numbers, and apply these properties. The absolute value of a + bi is written | a + bi |, and the formula for | a + bi |. Absolute Value With Imaginary Numbers.
From www.cuemath.com
Absolute Value Meaning, Sign, Examples How to Find Absolute Value? Absolute Value With Imaginary Numbers Understand the action of taking the conjugate of a. Complex numbers can have an absolute value of 1. The absolute value of a complex number, a + bi (also called the modulus) is defined as the distance between the origin (0, 0) and the point (a, b) in the complex plane. For a complex number in polar form r (cos. Absolute Value With Imaginary Numbers.
From www.examples.com
Absolute Value Examples, Function, Properties Absolute Value With Imaginary Numbers For a complex number in polar form r (cos θ + i sin θ). The absolute value of a complex number, a + bi (also called the modulus) is defined as the distance between the origin (0, 0) and the point (a, b) in the complex plane. Understand the action of taking the conjugate of a. Complex numbers can have. Absolute Value With Imaginary Numbers.
From sciencenotes.org
What Is Absolute Value? Definition and Examples Absolute Value With Imaginary Numbers Absolute value of complex numbers explained with diagrams, examples several practice problems. This is because all of them are one unit away from 0, either on. Understand the action of taking the conjugate of a. The absolute value of a complex number, a + bi (also called the modulus) is defined as the distance between the origin (0, 0) and. Absolute Value With Imaginary Numbers.
From funrithmetic.com
absolute value of complex numbers Funrithmetic Absolute Value With Imaginary Numbers Absolute value of complex numbers explained with diagrams, examples several practice problems. The absolute value of a complex number, a + bi (also called the modulus) is defined as the distance between the origin (0, 0) and the point (a, b) in the complex plane. This is because all of them are one unit away from 0, either on. Complex. Absolute Value With Imaginary Numbers.
From www.youtube.com
Absolute value of a complex number Imaginary and complex numbers Absolute Value With Imaginary Numbers For a complex number in polar form r (cos θ + i sin θ). Complex numbers can have an absolute value of 1. Absolute value of complex numbers explained with diagrams, examples several practice problems. Understand the action of taking the conjugate of a. The absolute value of a + bi is written | a + bi |, and the. Absolute Value With Imaginary Numbers.
From www.youtube.com
Day 3 HW (15 to 20) Finding the Absolute Value of a Complex (Imaginary Absolute Value With Imaginary Numbers The absolute value of a complex number, a + bi (also called the modulus) is defined as the distance between the origin (0, 0) and the point (a, b) in the complex plane. Complex numbers can have an absolute value of 1. Prove algebraic properties of addition and multiplication of complex numbers, and apply these properties. Absolute value of complex. Absolute Value With Imaginary Numbers.
From www.wikihow.com
How to Find the Absolute Value of a Number 15 Steps Absolute Value With Imaginary Numbers This is because all of them are one unit away from 0, either on. Absolute value of complex numbers explained with diagrams, examples several practice problems. The absolute value of a + bi is written | a + bi |, and the formula for | a + bi | is √a2+b2 a 2 + b 2. Complex numbers can have. Absolute Value With Imaginary Numbers.
From www.codingem.com
Python Absolute Value 'abs()' — A Complete Guide (with Examples) Absolute Value With Imaginary Numbers For a complex number in polar form r (cos θ + i sin θ). The absolute value of a + bi is written | a + bi |, and the formula for | a + bi | is √a2+b2 a 2 + b 2. Understand the action of taking the conjugate of a. Prove algebraic properties of addition and multiplication. Absolute Value With Imaginary Numbers.
From writeatopic.com
Absolute Value of Complex Numbers Write A Topic Absolute Value With Imaginary Numbers The absolute value of a + bi is written | a + bi |, and the formula for | a + bi | is √a2+b2 a 2 + b 2. The absolute value of a complex number, a + bi (also called the modulus) is defined as the distance between the origin (0, 0) and the point (a, b) in. Absolute Value With Imaginary Numbers.
From www.slideserve.com
PPT QUADRATIC FUNCTIONS PowerPoint Presentation, free download ID Absolute Value With Imaginary Numbers This is because all of them are one unit away from 0, either on. The absolute value of a complex number, a + bi (also called the modulus) is defined as the distance between the origin (0, 0) and the point (a, b) in the complex plane. Understand the action of taking the conjugate of a. The absolute value of. Absolute Value With Imaginary Numbers.
From www.showme.com
Absolute Value of Complex Number Math, Algebra, Algebra 2, Complex Absolute Value With Imaginary Numbers The absolute value of a complex number, a + bi (also called the modulus) is defined as the distance between the origin (0, 0) and the point (a, b) in the complex plane. This is because all of them are one unit away from 0, either on. The absolute value of a + bi is written | a + bi. Absolute Value With Imaginary Numbers.
From www.tes.com
Complex Numbers Absolute Value Poster Teaching Resources Absolute Value With Imaginary Numbers Prove algebraic properties of addition and multiplication of complex numbers, and apply these properties. For a complex number in polar form r (cos θ + i sin θ). The absolute value of a + bi is written | a + bi |, and the formula for | a + bi | is √a2+b2 a 2 + b 2. Understand the. Absolute Value With Imaginary Numbers.
From www.scribd.com
Chapter 1 Absolute Value & Complex Numbers PDF Complex Number Absolute Value With Imaginary Numbers Prove algebraic properties of addition and multiplication of complex numbers, and apply these properties. For a complex number in polar form r (cos θ + i sin θ). Understand the action of taking the conjugate of a. Complex numbers can have an absolute value of 1. Absolute value of complex numbers explained with diagrams, examples several practice problems. The absolute. Absolute Value With Imaginary Numbers.
From www.numerade.com
SOLVEDPlot the complex number and find its absolute value. 512 i Absolute Value With Imaginary Numbers The absolute value of a + bi is written | a + bi |, and the formula for | a + bi | is √a2+b2 a 2 + b 2. The absolute value of a complex number, a + bi (also called the modulus) is defined as the distance between the origin (0, 0) and the point (a, b) in. Absolute Value With Imaginary Numbers.
From www.youtube.com
Absolute Value of a Complex Number YouTube Absolute Value With Imaginary Numbers Prove algebraic properties of addition and multiplication of complex numbers, and apply these properties. Absolute value of complex numbers explained with diagrams, examples several practice problems. Complex numbers can have an absolute value of 1. This is because all of them are one unit away from 0, either on. Understand the action of taking the conjugate of a. The absolute. Absolute Value With Imaginary Numbers.
From funrithmetic.com
Absolute Value of Complex Numbers Color by Number Funrithmetic Absolute Value With Imaginary Numbers Prove algebraic properties of addition and multiplication of complex numbers, and apply these properties. Complex numbers can have an absolute value of 1. The absolute value of a complex number, a + bi (also called the modulus) is defined as the distance between the origin (0, 0) and the point (a, b) in the complex plane. Absolute value of complex. Absolute Value With Imaginary Numbers.
From mathmonks.com
Absolute Value of a Complex Number Definition, Formula, & Examples Absolute Value With Imaginary Numbers Understand the action of taking the conjugate of a. Complex numbers can have an absolute value of 1. Prove algebraic properties of addition and multiplication of complex numbers, and apply these properties. For a complex number in polar form r (cos θ + i sin θ). Absolute value of complex numbers explained with diagrams, examples several practice problems. The absolute. Absolute Value With Imaginary Numbers.
From www.youtube.com
Absolute Value Complex Numbers al2 Algebra 2 Abs1 YouTube Absolute Value With Imaginary Numbers Complex numbers can have an absolute value of 1. Understand the action of taking the conjugate of a. For a complex number in polar form r (cos θ + i sin θ). Absolute value of complex numbers explained with diagrams, examples several practice problems. Prove algebraic properties of addition and multiplication of complex numbers, and apply these properties. This is. Absolute Value With Imaginary Numbers.
From www.youtube.com
find absolute value of imaginary numbers YouTube Absolute Value With Imaginary Numbers The absolute value of a + bi is written | a + bi |, and the formula for | a + bi | is √a2+b2 a 2 + b 2. Absolute value of complex numbers explained with diagrams, examples several practice problems. Understand the action of taking the conjugate of a. For a complex number in polar form r (cos. Absolute Value With Imaginary Numbers.
From www.youtube.com
Absolute Value of Imaginary (Or Complex) Numbers YouTube Absolute Value With Imaginary Numbers Absolute value of complex numbers explained with diagrams, examples several practice problems. Prove algebraic properties of addition and multiplication of complex numbers, and apply these properties. For a complex number in polar form r (cos θ + i sin θ). The absolute value of a complex number, a + bi (also called the modulus) is defined as the distance between. Absolute Value With Imaginary Numbers.