Compression Deflection Equation at Levi Preston blog

Compression Deflection Equation. • for a given column section: L = load or force in psi. 3.2a, it is possible to observe that longitudinal elements of the beam near the bottom are stretched and those. Examining the deflection shape of fig. Hooke's law describes the relationship between the force applied to a spring and its extension or compression. Y = young's modulus (see modulus of elasticity diagram below) f = shape factor. L=d x y x (1+2f 2) d = % of deflection/inch of thickness. The central deflection \(w_o = v(x = \frac{l}{2}) \) is \[w_o = \frac{fl^3}{48.7ei}\frac{1}{1 − \frac{p}{p_c}} \label{10.31}\] for zero axial load, equation \ref{10.31} predicts a linear relation between. *the shape factor is determined. This section covers shear force and bending moment in beams, shear and moment diagrams, stresses in beams, and a table of common beam deflection formulas.

Hooke's law describes the relationship between the force applied to a spring and its extension or compression. 3.2a, it is possible to observe that longitudinal elements of the beam near the bottom are stretched and those. Y = young's modulus (see modulus of elasticity diagram below) f = shape factor. • for a given column section: The central deflection \(w_o = v(x = \frac{l}{2}) \) is \[w_o = \frac{fl^3}{48.7ei}\frac{1}{1 − \frac{p}{p_c}} \label{10.31}\] for zero axial load, equation \ref{10.31} predicts a linear relation between. L=d x y x (1+2f 2) d = % of deflection/inch of thickness. L = load or force in psi. *the shape factor is determined. This section covers shear force and bending moment in beams, shear and moment diagrams, stresses in beams, and a table of common beam deflection formulas. Examining the deflection shape of fig.

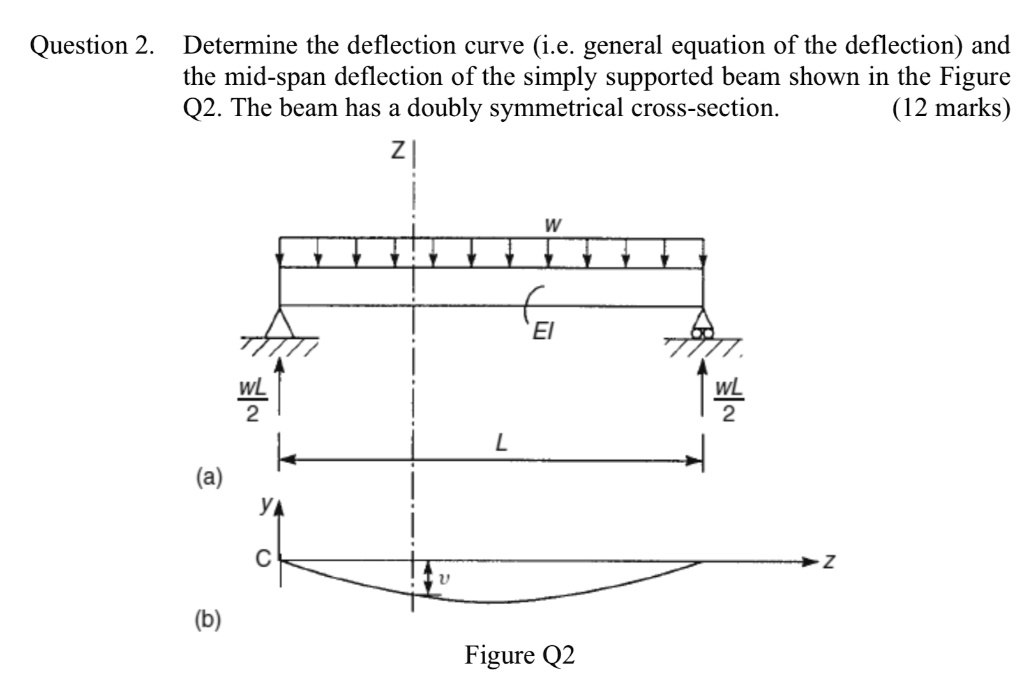
SOLVED Determine the deflection curve (i.e. general equation of the

Compression Deflection Equation Y = young's modulus (see modulus of elasticity diagram below) f = shape factor. Examining the deflection shape of fig. Hooke's law describes the relationship between the force applied to a spring and its extension or compression. *the shape factor is determined. 3.2a, it is possible to observe that longitudinal elements of the beam near the bottom are stretched and those. • for a given column section: This section covers shear force and bending moment in beams, shear and moment diagrams, stresses in beams, and a table of common beam deflection formulas. The central deflection \(w_o = v(x = \frac{l}{2}) \) is \[w_o = \frac{fl^3}{48.7ei}\frac{1}{1 − \frac{p}{p_c}} \label{10.31}\] for zero axial load, equation \ref{10.31} predicts a linear relation between. L = load or force in psi. L=d x y x (1+2f 2) d = % of deflection/inch of thickness. Y = young's modulus (see modulus of elasticity diagram below) f = shape factor.