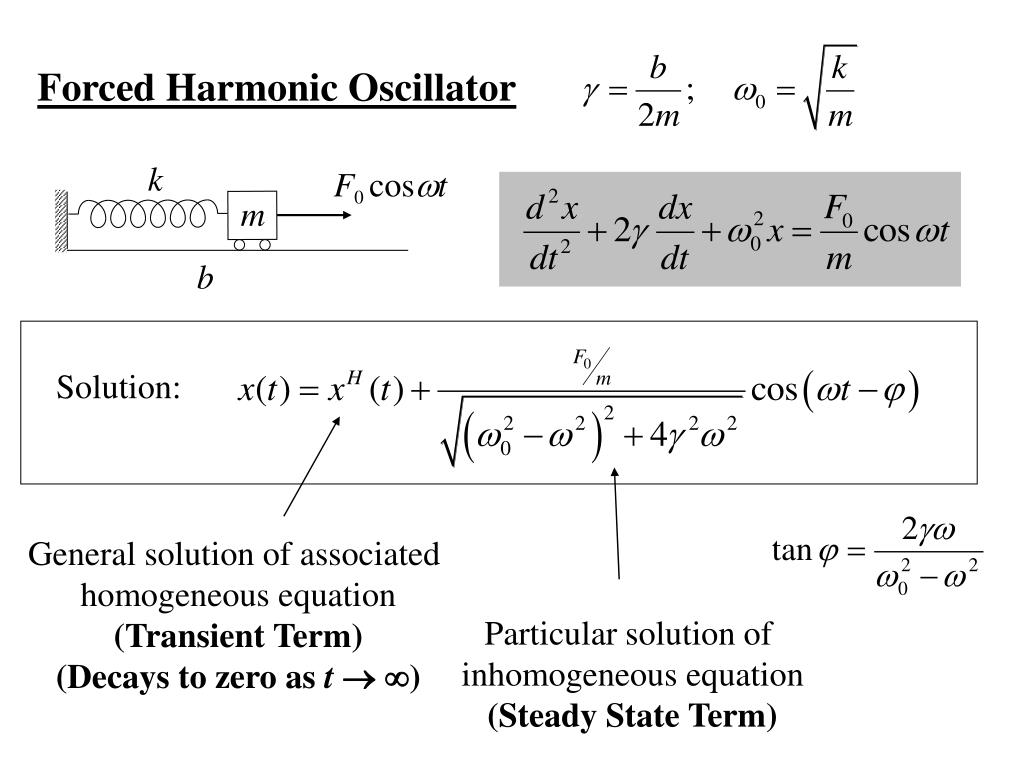
Forced Oscillator Solution at Madison Hales blog

Forced Oscillator Solution. The solution to is given by the function \[x(t)=x_{0} \cos (\omega t+\phi) \nonumber \] where the amplitude \(x_{0}\) is a function of the driving angular frequency ω and is given by Hence \( a = 0 \) and \( b = \frac {f_0}{2m \omega } \). Our particular solution is \( \frac {f_0}{2m \omega } t \sin (\omega t) \) and our general solution is \[ x = c_1 \cos (\omega t) + c_2 \sin (\omega t) + \frac {f_0}{2m \omega } t \sin (\omega t) \nonumber \] the important term is the last one (the particular solution we found). Explain the concept of resonance and its. This problem set provides practice in understanding damped harmonic oscillator systems, solving forced oscillator equations,. Our desired solution can be found by taking the real projection \[x(t)=\operatorname{re}(z(t))=x_{0} \cos. List the equations of motion associated with forced oscillations. Solution to the forced damped oscillator equation. We derive the solution to equation (23.6.4) in appendix 23e: List the equations of motion associated with forced oscillations; List the equations of motion associated with forced oscillations; Explain the concept of resonance and its. Explain the concept of resonance and its.

The solution to is given by the function \[x(t)=x_{0} \cos (\omega t+\phi) \nonumber \] where the amplitude \(x_{0}\) is a function of the driving angular frequency ω and is given by List the equations of motion associated with forced oscillations; Our particular solution is \( \frac {f_0}{2m \omega } t \sin (\omega t) \) and our general solution is \[ x = c_1 \cos (\omega t) + c_2 \sin (\omega t) + \frac {f_0}{2m \omega } t \sin (\omega t) \nonumber \] the important term is the last one (the particular solution we found). Explain the concept of resonance and its. Explain the concept of resonance and its. Our desired solution can be found by taking the real projection \[x(t)=\operatorname{re}(z(t))=x_{0} \cos. Solution to the forced damped oscillator equation. Hence \( a = 0 \) and \( b = \frac {f_0}{2m \omega } \). We derive the solution to equation (23.6.4) in appendix 23e: This problem set provides practice in understanding damped harmonic oscillator systems, solving forced oscillator equations,.

PPT Forced Harmonic Oscillator PowerPoint Presentation, free download

Forced Oscillator Solution This problem set provides practice in understanding damped harmonic oscillator systems, solving forced oscillator equations,. Our desired solution can be found by taking the real projection \[x(t)=\operatorname{re}(z(t))=x_{0} \cos. List the equations of motion associated with forced oscillations; List the equations of motion associated with forced oscillations; We derive the solution to equation (23.6.4) in appendix 23e: This problem set provides practice in understanding damped harmonic oscillator systems, solving forced oscillator equations,. Explain the concept of resonance and its. Our particular solution is \( \frac {f_0}{2m \omega } t \sin (\omega t) \) and our general solution is \[ x = c_1 \cos (\omega t) + c_2 \sin (\omega t) + \frac {f_0}{2m \omega } t \sin (\omega t) \nonumber \] the important term is the last one (the particular solution we found). Explain the concept of resonance and its. Hence \( a = 0 \) and \( b = \frac {f_0}{2m \omega } \). List the equations of motion associated with forced oscillations. Solution to the forced damped oscillator equation. Explain the concept of resonance and its. The solution to is given by the function \[x(t)=x_{0} \cos (\omega t+\phi) \nonumber \] where the amplitude \(x_{0}\) is a function of the driving angular frequency ω and is given by