Extension Of Series Springs . Allowing for the free length of the. Up to a level you only have to consider sets of identical springs making up series and parallel combinations. Springs in series and parallel. The extension, then, for both springs is x = (0.24 n)/(1 n/m), or 24 cm, half the extension for the single spring. The formula for the equivalent spring constant can be extended to a system of n springs in a series combination. Two springs of equal spring constant k are combined in series and in parallel. By measuring the extension of the spring combination one can determine the effective spring constants: I'm trying to understand why the energy stored in a set of series springs is different from the energy stored in parallel springs.
from www.chegg.com
Springs in series and parallel. The formula for the equivalent spring constant can be extended to a system of n springs in a series combination. Two springs of equal spring constant k are combined in series and in parallel. Up to a level you only have to consider sets of identical springs making up series and parallel combinations. The extension, then, for both springs is x = (0.24 n)/(1 n/m), or 24 cm, half the extension for the single spring. I'm trying to understand why the energy stored in a set of series springs is different from the energy stored in parallel springs. By measuring the extension of the spring combination one can determine the effective spring constants: Allowing for the free length of the.
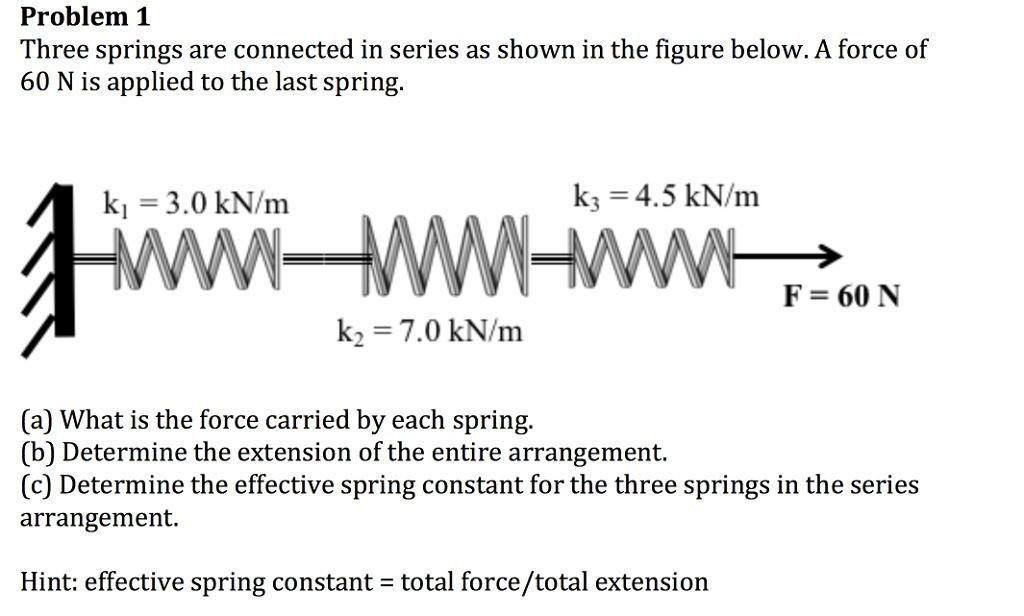
Solved Problem 1 Three springs are connected in series as
Extension Of Series Springs Two springs of equal spring constant k are combined in series and in parallel. Allowing for the free length of the. The formula for the equivalent spring constant can be extended to a system of n springs in a series combination. Springs in series and parallel. Up to a level you only have to consider sets of identical springs making up series and parallel combinations. Two springs of equal spring constant k are combined in series and in parallel. I'm trying to understand why the energy stored in a set of series springs is different from the energy stored in parallel springs. By measuring the extension of the spring combination one can determine the effective spring constants: The extension, then, for both springs is x = (0.24 n)/(1 n/m), or 24 cm, half the extension for the single spring.
From www.msspring.com
Custom Extension Springs M & S Spring Extension Of Series Springs I'm trying to understand why the energy stored in a set of series springs is different from the energy stored in parallel springs. Two springs of equal spring constant k are combined in series and in parallel. The extension, then, for both springs is x = (0.24 n)/(1 n/m), or 24 cm, half the extension for the single spring. Up. Extension Of Series Springs.
From www.slideshare.net
Springs Extension Of Series Springs I'm trying to understand why the energy stored in a set of series springs is different from the energy stored in parallel springs. Up to a level you only have to consider sets of identical springs making up series and parallel combinations. Two springs of equal spring constant k are combined in series and in parallel. Springs in series and. Extension Of Series Springs.
From www.savemyexams.com
Hooke's Law CIE A Level Physics Revision Notes 2022 Extension Of Series Springs I'm trying to understand why the energy stored in a set of series springs is different from the energy stored in parallel springs. The formula for the equivalent spring constant can be extended to a system of n springs in a series combination. The extension, then, for both springs is x = (0.24 n)/(1 n/m), or 24 cm, half the. Extension Of Series Springs.
From www.iqsdirectory.com
Extension Spring Types, Uses, Features and Benefits Extension Of Series Springs Springs in series and parallel. The extension, then, for both springs is x = (0.24 n)/(1 n/m), or 24 cm, half the extension for the single spring. Allowing for the free length of the. Two springs of equal spring constant k are combined in series and in parallel. Up to a level you only have to consider sets of identical. Extension Of Series Springs.
From demonstrations.wolfram.com
Springs in Parallel and in Series Wolfram Demonstrations Project Extension Of Series Springs The formula for the equivalent spring constant can be extended to a system of n springs in a series combination. Springs in series and parallel. The extension, then, for both springs is x = (0.24 n)/(1 n/m), or 24 cm, half the extension for the single spring. Up to a level you only have to consider sets of identical springs. Extension Of Series Springs.
From www.youtube.com
APC Lesson 48 Effective k of springs in series, parallel YouTube Extension Of Series Springs The formula for the equivalent spring constant can be extended to a system of n springs in a series combination. Up to a level you only have to consider sets of identical springs making up series and parallel combinations. By measuring the extension of the spring combination one can determine the effective spring constants: The extension, then, for both springs. Extension Of Series Springs.
From www.youtube.com
Spring constants in series and parallel YouTube Extension Of Series Springs Up to a level you only have to consider sets of identical springs making up series and parallel combinations. The formula for the equivalent spring constant can be extended to a system of n springs in a series combination. Allowing for the free length of the. By measuring the extension of the spring combination one can determine the effective spring. Extension Of Series Springs.
From www.pspring.com
Springs Compression, Extension, Torsion Peterson Spring Extension Of Series Springs Springs in series and parallel. Two springs of equal spring constant k are combined in series and in parallel. The extension, then, for both springs is x = (0.24 n)/(1 n/m), or 24 cm, half the extension for the single spring. I'm trying to understand why the energy stored in a set of series springs is different from the energy. Extension Of Series Springs.
From scienceres-edcp-educ.sites.olt.ubc.ca
Springs MSTLTT Extension Of Series Springs The extension, then, for both springs is x = (0.24 n)/(1 n/m), or 24 cm, half the extension for the single spring. Up to a level you only have to consider sets of identical springs making up series and parallel combinations. The formula for the equivalent spring constant can be extended to a system of n springs in a series. Extension Of Series Springs.
From www.youtube.com
Simple Harmonic Motion Springs in series vs parallel, and vertical Extension Of Series Springs The formula for the equivalent spring constant can be extended to a system of n springs in a series combination. Springs in series and parallel. Up to a level you only have to consider sets of identical springs making up series and parallel combinations. I'm trying to understand why the energy stored in a set of series springs is different. Extension Of Series Springs.
From www.doubtnut.com
Exercise Of SpringParallel Combination Of Spring Extension Of Series Springs Up to a level you only have to consider sets of identical springs making up series and parallel combinations. By measuring the extension of the spring combination one can determine the effective spring constants: I'm trying to understand why the energy stored in a set of series springs is different from the energy stored in parallel springs. Allowing for the. Extension Of Series Springs.
From www.chegg.com
Solved Problem 1 Three springs are connected in series as Extension Of Series Springs I'm trying to understand why the energy stored in a set of series springs is different from the energy stored in parallel springs. Springs in series and parallel. By measuring the extension of the spring combination one can determine the effective spring constants: The formula for the equivalent spring constant can be extended to a system of n springs in. Extension Of Series Springs.
From studylib.net
Combinations of Springs Springs in Series Extension Of Series Springs Allowing for the free length of the. Two springs of equal spring constant k are combined in series and in parallel. Springs in series and parallel. Up to a level you only have to consider sets of identical springs making up series and parallel combinations. The extension, then, for both springs is x = (0.24 n)/(1 n/m), or 24 cm,. Extension Of Series Springs.
From www.thestudentroom.co.uk
Springs in series/parallel, please help!!! The Student Room Extension Of Series Springs I'm trying to understand why the energy stored in a set of series springs is different from the energy stored in parallel springs. The extension, then, for both springs is x = (0.24 n)/(1 n/m), or 24 cm, half the extension for the single spring. Springs in series and parallel. Allowing for the free length of the. Up to a. Extension Of Series Springs.
From www.youtube.com
Extension Springs Maximum Elongation Example 1 YouTube Extension Of Series Springs The formula for the equivalent spring constant can be extended to a system of n springs in a series combination. Two springs of equal spring constant k are combined in series and in parallel. By measuring the extension of the spring combination one can determine the effective spring constants: Up to a level you only have to consider sets of. Extension Of Series Springs.
From www.rmwindustries.com
Extension Springs RMW Industries Extension Of Series Springs By measuring the extension of the spring combination one can determine the effective spring constants: Up to a level you only have to consider sets of identical springs making up series and parallel combinations. Two springs of equal spring constant k are combined in series and in parallel. The extension, then, for both springs is x = (0.24 n)/(1 n/m),. Extension Of Series Springs.
From isaacphysics.org
Isaac Physics Extension Of Series Springs The formula for the equivalent spring constant can be extended to a system of n springs in a series combination. Two springs of equal spring constant k are combined in series and in parallel. The extension, then, for both springs is x = (0.24 n)/(1 n/m), or 24 cm, half the extension for the single spring. Up to a level. Extension Of Series Springs.
From www.doubtnut.com
Two identical springs are connected in series and parallel as shown in Extension Of Series Springs The extension, then, for both springs is x = (0.24 n)/(1 n/m), or 24 cm, half the extension for the single spring. I'm trying to understand why the energy stored in a set of series springs is different from the energy stored in parallel springs. By measuring the extension of the spring combination one can determine the effective spring constants:. Extension Of Series Springs.
From ajaxsprings.com
Extension Springs What You Need to Know Ajax Wire & Spring Extension Of Series Springs The extension, then, for both springs is x = (0.24 n)/(1 n/m), or 24 cm, half the extension for the single spring. Two springs of equal spring constant k are combined in series and in parallel. Allowing for the free length of the. Springs in series and parallel. Up to a level you only have to consider sets of identical. Extension Of Series Springs.
From www.pspring.com
Springs Compression, Extension, Torsion Peterson Spring Extension Of Series Springs Allowing for the free length of the. By measuring the extension of the spring combination one can determine the effective spring constants: The extension, then, for both springs is x = (0.24 n)/(1 n/m), or 24 cm, half the extension for the single spring. Springs in series and parallel. Up to a level you only have to consider sets of. Extension Of Series Springs.
From www.mech4study.com
What is Spring? What are Types of Springs? mech4study Extension Of Series Springs Springs in series and parallel. The formula for the equivalent spring constant can be extended to a system of n springs in a series combination. Allowing for the free length of the. I'm trying to understand why the energy stored in a set of series springs is different from the energy stored in parallel springs. Up to a level you. Extension Of Series Springs.
From www.youtube.com
How to solve series and parallel spring (Hooke's law) YouTube Extension Of Series Springs Up to a level you only have to consider sets of identical springs making up series and parallel combinations. By measuring the extension of the spring combination one can determine the effective spring constants: The formula for the equivalent spring constant can be extended to a system of n springs in a series combination. Two springs of equal spring constant. Extension Of Series Springs.
From aimcoil.com
The Physics of Springs How Manufacturers Understand Spring Design Extension Of Series Springs The formula for the equivalent spring constant can be extended to a system of n springs in a series combination. I'm trying to understand why the energy stored in a set of series springs is different from the energy stored in parallel springs. The extension, then, for both springs is x = (0.24 n)/(1 n/m), or 24 cm, half the. Extension Of Series Springs.
From www.youtube.com
Parallel and Series Springs YouTube Extension Of Series Springs By measuring the extension of the spring combination one can determine the effective spring constants: The formula for the equivalent spring constant can be extended to a system of n springs in a series combination. I'm trying to understand why the energy stored in a set of series springs is different from the energy stored in parallel springs. Springs in. Extension Of Series Springs.
From www.youtube.com
6.2b Ex1 FM19 P12 Q20 Springs Extension in Series AS Deformation Extension Of Series Springs Up to a level you only have to consider sets of identical springs making up series and parallel combinations. Two springs of equal spring constant k are combined in series and in parallel. I'm trying to understand why the energy stored in a set of series springs is different from the energy stored in parallel springs. Springs in series and. Extension Of Series Springs.
From www.youtube.com
2of6 hooke's law and combination of springs YouTube Extension Of Series Springs Springs in series and parallel. Allowing for the free length of the. The formula for the equivalent spring constant can be extended to a system of n springs in a series combination. Two springs of equal spring constant k are combined in series and in parallel. The extension, then, for both springs is x = (0.24 n)/(1 n/m), or 24. Extension Of Series Springs.
From www.slideserve.com
PPT Pulleys, Strings, Springs and Things Part 2 PowerPoint Extension Of Series Springs The formula for the equivalent spring constant can be extended to a system of n springs in a series combination. By measuring the extension of the spring combination one can determine the effective spring constants: Up to a level you only have to consider sets of identical springs making up series and parallel combinations. Two springs of equal spring constant. Extension Of Series Springs.
From tillescenter.org
Extension Spring tillescenter Power Transmission Products Springs Extension Of Series Springs The extension, then, for both springs is x = (0.24 n)/(1 n/m), or 24 cm, half the extension for the single spring. Springs in series and parallel. Allowing for the free length of the. Up to a level you only have to consider sets of identical springs making up series and parallel combinations. The formula for the equivalent spring constant. Extension Of Series Springs.
From coosprings.com
EXTENSION SPRINGS cooprings Extension Of Series Springs The extension, then, for both springs is x = (0.24 n)/(1 n/m), or 24 cm, half the extension for the single spring. The formula for the equivalent spring constant can be extended to a system of n springs in a series combination. Springs in series and parallel. By measuring the extension of the spring combination one can determine the effective. Extension Of Series Springs.
From www.walmart.com
Handyman Extension Spring, 1/4 in. x 11/2 in. x 0.035 in., Steel Extension Of Series Springs Up to a level you only have to consider sets of identical springs making up series and parallel combinations. I'm trying to understand why the energy stored in a set of series springs is different from the energy stored in parallel springs. The extension, then, for both springs is x = (0.24 n)/(1 n/m), or 24 cm, half the extension. Extension Of Series Springs.
From www.masterspring.com
What Is an Extension Spring & What Is It Used For? Master Spring Extension Of Series Springs Springs in series and parallel. By measuring the extension of the spring combination one can determine the effective spring constants: I'm trying to understand why the energy stored in a set of series springs is different from the energy stored in parallel springs. The formula for the equivalent spring constant can be extended to a system of n springs in. Extension Of Series Springs.
From www.springsfast.com
Hooke’s Law and the Science Behind Springs WB Jones Extension Of Series Springs The extension, then, for both springs is x = (0.24 n)/(1 n/m), or 24 cm, half the extension for the single spring. I'm trying to understand why the energy stored in a set of series springs is different from the energy stored in parallel springs. Up to a level you only have to consider sets of identical springs making up. Extension Of Series Springs.
From www.youtube.com
Springs in Series Verse Parallel Find Spring Constant YouTube Extension Of Series Springs Springs in series and parallel. The extension, then, for both springs is x = (0.24 n)/(1 n/m), or 24 cm, half the extension for the single spring. Allowing for the free length of the. Two springs of equal spring constant k are combined in series and in parallel. Up to a level you only have to consider sets of identical. Extension Of Series Springs.
From www.valleyspring.com
Heavy Duty Extension Springs Extension Of Series Springs Two springs of equal spring constant k are combined in series and in parallel. Springs in series and parallel. Up to a level you only have to consider sets of identical springs making up series and parallel combinations. I'm trying to understand why the energy stored in a set of series springs is different from the energy stored in parallel. Extension Of Series Springs.
From tillescenter.org
Extension Spring tillescenter Power Transmission Products Springs Extension Of Series Springs Two springs of equal spring constant k are combined in series and in parallel. Springs in series and parallel. Allowing for the free length of the. By measuring the extension of the spring combination one can determine the effective spring constants: I'm trying to understand why the energy stored in a set of series springs is different from the energy. Extension Of Series Springs.