Define Uniform Function . But your interpretation is rather correct:. A sequence of functions { fn(x) } with domain d converges uniformly to a function f (x) if given any > 0 there is a. D \rightarrow \mathbb{r}\) is called uniformly continuous on \(d\) if for any \(\varepsilon > 0\), there exists \(\delta > 0\). That makes a big difference. Evaluating whether a function is uniformly continuous requires applying the mathematical definition of uniform continuity,. For $n \in \mathbb{n}$, define the formula, $$f_n(x)= \frac{x}{2n^2x^2+8},\quad x \in [0,1].$$ prove that the sequence $f_n$ converges. First of all, continuity is defined at a point $c$, whereas uniform continuity is defined on a set $a$.
from www.slideserve.com
Evaluating whether a function is uniformly continuous requires applying the mathematical definition of uniform continuity,. But your interpretation is rather correct:. For $n \in \mathbb{n}$, define the formula, $$f_n(x)= \frac{x}{2n^2x^2+8},\quad x \in [0,1].$$ prove that the sequence $f_n$ converges. That makes a big difference. A sequence of functions { fn(x) } with domain d converges uniformly to a function f (x) if given any > 0 there is a. D \rightarrow \mathbb{r}\) is called uniformly continuous on \(d\) if for any \(\varepsilon > 0\), there exists \(\delta > 0\). First of all, continuity is defined at a point $c$, whereas uniform continuity is defined on a set $a$.
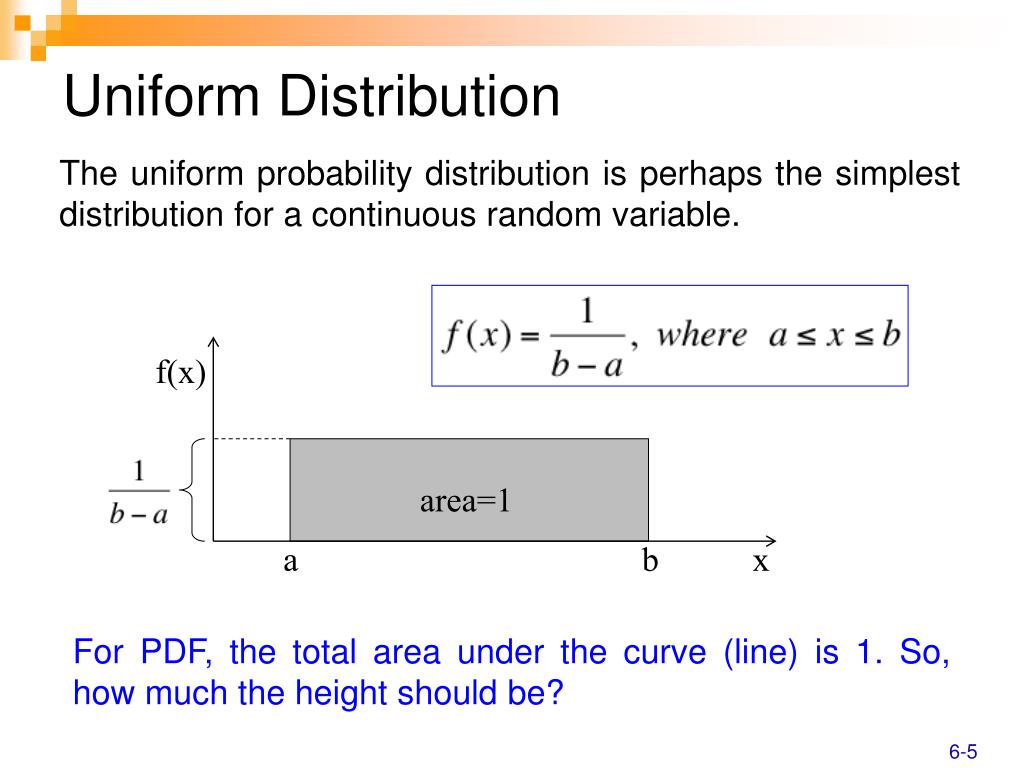
PPT Continuous Probability Distributions PowerPoint Presentation
Define Uniform Function Evaluating whether a function is uniformly continuous requires applying the mathematical definition of uniform continuity,. Evaluating whether a function is uniformly continuous requires applying the mathematical definition of uniform continuity,. First of all, continuity is defined at a point $c$, whereas uniform continuity is defined on a set $a$. But your interpretation is rather correct:. For $n \in \mathbb{n}$, define the formula, $$f_n(x)= \frac{x}{2n^2x^2+8},\quad x \in [0,1].$$ prove that the sequence $f_n$ converges. D \rightarrow \mathbb{r}\) is called uniformly continuous on \(d\) if for any \(\varepsilon > 0\), there exists \(\delta > 0\). That makes a big difference. A sequence of functions { fn(x) } with domain d converges uniformly to a function f (x) if given any > 0 there is a.
From www.youtube.com
Uniform distribution cumulative distribution function YouTube Define Uniform Function Evaluating whether a function is uniformly continuous requires applying the mathematical definition of uniform continuity,. A sequence of functions { fn(x) } with domain d converges uniformly to a function f (x) if given any > 0 there is a. First of all, continuity is defined at a point $c$, whereas uniform continuity is defined on a set $a$. D. Define Uniform Function.
From www.slideserve.com
PPT MEAN AND VARIANCE OF A DISTRIBUTION PowerPoint Presentation, free Define Uniform Function A sequence of functions { fn(x) } with domain d converges uniformly to a function f (x) if given any > 0 there is a. First of all, continuity is defined at a point $c$, whereas uniform continuity is defined on a set $a$. That makes a big difference. Evaluating whether a function is uniformly continuous requires applying the mathematical. Define Uniform Function.
From calcworkshop.com
Discrete Uniform Distribution (w/ 5+ Worked Examples!) Define Uniform Function D \rightarrow \mathbb{r}\) is called uniformly continuous on \(d\) if for any \(\varepsilon > 0\), there exists \(\delta > 0\). For $n \in \mathbb{n}$, define the formula, $$f_n(x)= \frac{x}{2n^2x^2+8},\quad x \in [0,1].$$ prove that the sequence $f_n$ converges. That makes a big difference. First of all, continuity is defined at a point $c$, whereas uniform continuity is defined on a. Define Uniform Function.
From www.statology.org
An Introduction to the Uniform Distribution Define Uniform Function That makes a big difference. For $n \in \mathbb{n}$, define the formula, $$f_n(x)= \frac{x}{2n^2x^2+8},\quad x \in [0,1].$$ prove that the sequence $f_n$ converges. A sequence of functions { fn(x) } with domain d converges uniformly to a function f (x) if given any > 0 there is a. But your interpretation is rather correct:. First of all, continuity is defined. Define Uniform Function.
From www.slideserve.com
PPT Continuous distributions PowerPoint Presentation, free download Define Uniform Function But your interpretation is rather correct:. First of all, continuity is defined at a point $c$, whereas uniform continuity is defined on a set $a$. A sequence of functions { fn(x) } with domain d converges uniformly to a function f (x) if given any > 0 there is a. That makes a big difference. For $n \in \mathbb{n}$, define. Define Uniform Function.
From vasttechno.weebly.com
Cdf of a uniform distribution vasttechno Define Uniform Function D \rightarrow \mathbb{r}\) is called uniformly continuous on \(d\) if for any \(\varepsilon > 0\), there exists \(\delta > 0\). Evaluating whether a function is uniformly continuous requires applying the mathematical definition of uniform continuity,. For $n \in \mathbb{n}$, define the formula, $$f_n(x)= \frac{x}{2n^2x^2+8},\quad x \in [0,1].$$ prove that the sequence $f_n$ converges. But your interpretation is rather correct:. First. Define Uniform Function.
From www.investopedia.com
Uniform Distribution Definition, How It Works, and Example Define Uniform Function But your interpretation is rather correct:. A sequence of functions { fn(x) } with domain d converges uniformly to a function f (x) if given any > 0 there is a. That makes a big difference. Evaluating whether a function is uniformly continuous requires applying the mathematical definition of uniform continuity,. D \rightarrow \mathbb{r}\) is called uniformly continuous on \(d\). Define Uniform Function.
From www.youtube.com
uniform density function YouTube Define Uniform Function Evaluating whether a function is uniformly continuous requires applying the mathematical definition of uniform continuity,. First of all, continuity is defined at a point $c$, whereas uniform continuity is defined on a set $a$. D \rightarrow \mathbb{r}\) is called uniformly continuous on \(d\) if for any \(\varepsilon > 0\), there exists \(\delta > 0\). But your interpretation is rather correct:.. Define Uniform Function.
From www.vrogue.co
Uniform Distribution Definition How It Works And Exam vrogue.co Define Uniform Function D \rightarrow \mathbb{r}\) is called uniformly continuous on \(d\) if for any \(\varepsilon > 0\), there exists \(\delta > 0\). A sequence of functions { fn(x) } with domain d converges uniformly to a function f (x) if given any > 0 there is a. Evaluating whether a function is uniformly continuous requires applying the mathematical definition of uniform continuity,.. Define Uniform Function.
From www.vrogue.co
Uniform Distribution Definition How It Works And Exam vrogue.co Define Uniform Function D \rightarrow \mathbb{r}\) is called uniformly continuous on \(d\) if for any \(\varepsilon > 0\), there exists \(\delta > 0\). First of all, continuity is defined at a point $c$, whereas uniform continuity is defined on a set $a$. Evaluating whether a function is uniformly continuous requires applying the mathematical definition of uniform continuity,. But your interpretation is rather correct:.. Define Uniform Function.
From www.slideserve.com
PPT Continuous Probability Distributions PowerPoint Presentation Define Uniform Function Evaluating whether a function is uniformly continuous requires applying the mathematical definition of uniform continuity,. D \rightarrow \mathbb{r}\) is called uniformly continuous on \(d\) if for any \(\varepsilon > 0\), there exists \(\delta > 0\). A sequence of functions { fn(x) } with domain d converges uniformly to a function f (x) if given any > 0 there is a.. Define Uniform Function.
From www.youtube.com
Uniform distribution (discrete) YouTube Define Uniform Function But your interpretation is rather correct:. A sequence of functions { fn(x) } with domain d converges uniformly to a function f (x) if given any > 0 there is a. That makes a big difference. Evaluating whether a function is uniformly continuous requires applying the mathematical definition of uniform continuity,. For $n \in \mathbb{n}$, define the formula, $$f_n(x)= \frac{x}{2n^2x^2+8},\quad. Define Uniform Function.
From www.youtube.com
Advanced Calculus Uniform Continuity Proof f(x) = x/(x 1) on [2 Define Uniform Function But your interpretation is rather correct:. That makes a big difference. For $n \in \mathbb{n}$, define the formula, $$f_n(x)= \frac{x}{2n^2x^2+8},\quad x \in [0,1].$$ prove that the sequence $f_n$ converges. A sequence of functions { fn(x) } with domain d converges uniformly to a function f (x) if given any > 0 there is a. D \rightarrow \mathbb{r}\) is called uniformly. Define Uniform Function.
From www.youtube.com
Deriving a formula for the mean of the uniform distribution YouTube Define Uniform Function That makes a big difference. For $n \in \mathbb{n}$, define the formula, $$f_n(x)= \frac{x}{2n^2x^2+8},\quad x \in [0,1].$$ prove that the sequence $f_n$ converges. D \rightarrow \mathbb{r}\) is called uniformly continuous on \(d\) if for any \(\varepsilon > 0\), there exists \(\delta > 0\). But your interpretation is rather correct:. Evaluating whether a function is uniformly continuous requires applying the mathematical. Define Uniform Function.
From analystprep.com
Properties of Continuous Uniform Distribution AnalystPrep CFA® Exam Define Uniform Function D \rightarrow \mathbb{r}\) is called uniformly continuous on \(d\) if for any \(\varepsilon > 0\), there exists \(\delta > 0\). First of all, continuity is defined at a point $c$, whereas uniform continuity is defined on a set $a$. A sequence of functions { fn(x) } with domain d converges uniformly to a function f (x) if given any >. Define Uniform Function.
From www.youtube.com
Continuous and Uniformly Continuous Functions YouTube Define Uniform Function That makes a big difference. Evaluating whether a function is uniformly continuous requires applying the mathematical definition of uniform continuity,. First of all, continuity is defined at a point $c$, whereas uniform continuity is defined on a set $a$. A sequence of functions { fn(x) } with domain d converges uniformly to a function f (x) if given any >. Define Uniform Function.
From www.slideserve.com
PPT Section 523 PowerPoint Presentation, free download ID2338800 Define Uniform Function That makes a big difference. First of all, continuity is defined at a point $c$, whereas uniform continuity is defined on a set $a$. Evaluating whether a function is uniformly continuous requires applying the mathematical definition of uniform continuity,. A sequence of functions { fn(x) } with domain d converges uniformly to a function f (x) if given any >. Define Uniform Function.
From dlsun.github.io
Lesson 34 Uniform Distribution Introduction to Probability Define Uniform Function But your interpretation is rather correct:. First of all, continuity is defined at a point $c$, whereas uniform continuity is defined on a set $a$. D \rightarrow \mathbb{r}\) is called uniformly continuous on \(d\) if for any \(\varepsilon > 0\), there exists \(\delta > 0\). For $n \in \mathbb{n}$, define the formula, $$f_n(x)= \frac{x}{2n^2x^2+8},\quad x \in [0,1].$$ prove that the. Define Uniform Function.
From www.vrogue.co
Uniform Distribution Definition How It Works And Exam vrogue.co Define Uniform Function Evaluating whether a function is uniformly continuous requires applying the mathematical definition of uniform continuity,. That makes a big difference. First of all, continuity is defined at a point $c$, whereas uniform continuity is defined on a set $a$. A sequence of functions { fn(x) } with domain d converges uniformly to a function f (x) if given any >. Define Uniform Function.
From www.youtube.com
Chapter 6 Introduction to the Uniform distribution YouTube Define Uniform Function But your interpretation is rather correct:. First of all, continuity is defined at a point $c$, whereas uniform continuity is defined on a set $a$. For $n \in \mathbb{n}$, define the formula, $$f_n(x)= \frac{x}{2n^2x^2+8},\quad x \in [0,1].$$ prove that the sequence $f_n$ converges. That makes a big difference. Evaluating whether a function is uniformly continuous requires applying the mathematical definition. Define Uniform Function.
From www.youtube.com
Uniform Distribution Mean, Variance and Moment Generating Function Define Uniform Function First of all, continuity is defined at a point $c$, whereas uniform continuity is defined on a set $a$. That makes a big difference. D \rightarrow \mathbb{r}\) is called uniformly continuous on \(d\) if for any \(\varepsilon > 0\), there exists \(\delta > 0\). A sequence of functions { fn(x) } with domain d converges uniformly to a function f. Define Uniform Function.
From analystprep.com
cfalevel1continuous uniform random variable AnalystPrep CFA Define Uniform Function D \rightarrow \mathbb{r}\) is called uniformly continuous on \(d\) if for any \(\varepsilon > 0\), there exists \(\delta > 0\). For $n \in \mathbb{n}$, define the formula, $$f_n(x)= \frac{x}{2n^2x^2+8},\quad x \in [0,1].$$ prove that the sequence $f_n$ converges. But your interpretation is rather correct:. Evaluating whether a function is uniformly continuous requires applying the mathematical definition of uniform continuity,. A. Define Uniform Function.
From elizabethyouthmckenzie.blogspot.com
Cdf of Uniform Distribution Define Uniform Function For $n \in \mathbb{n}$, define the formula, $$f_n(x)= \frac{x}{2n^2x^2+8},\quad x \in [0,1].$$ prove that the sequence $f_n$ converges. First of all, continuity is defined at a point $c$, whereas uniform continuity is defined on a set $a$. A sequence of functions { fn(x) } with domain d converges uniformly to a function f (x) if given any > 0 there. Define Uniform Function.
From www.youtube.com
Uniform distribution moment generating function YouTube Define Uniform Function First of all, continuity is defined at a point $c$, whereas uniform continuity is defined on a set $a$. For $n \in \mathbb{n}$, define the formula, $$f_n(x)= \frac{x}{2n^2x^2+8},\quad x \in [0,1].$$ prove that the sequence $f_n$ converges. D \rightarrow \mathbb{r}\) is called uniformly continuous on \(d\) if for any \(\varepsilon > 0\), there exists \(\delta > 0\). But your interpretation. Define Uniform Function.
From www.statisticalaid.com
Uniform Distribution definition, formula and applications Define Uniform Function First of all, continuity is defined at a point $c$, whereas uniform continuity is defined on a set $a$. A sequence of functions { fn(x) } with domain d converges uniformly to a function f (x) if given any > 0 there is a. D \rightarrow \mathbb{r}\) is called uniformly continuous on \(d\) if for any \(\varepsilon > 0\), there. Define Uniform Function.
From www.youtube.com
Continuous Uniform Distribution (3) E(X), Var(X), F(X Define Uniform Function For $n \in \mathbb{n}$, define the formula, $$f_n(x)= \frac{x}{2n^2x^2+8},\quad x \in [0,1].$$ prove that the sequence $f_n$ converges. That makes a big difference. But your interpretation is rather correct:. A sequence of functions { fn(x) } with domain d converges uniformly to a function f (x) if given any > 0 there is a. D \rightarrow \mathbb{r}\) is called uniformly. Define Uniform Function.
From www.youtube.com
Probability of Uniform Distribution Example YouTube Define Uniform Function First of all, continuity is defined at a point $c$, whereas uniform continuity is defined on a set $a$. D \rightarrow \mathbb{r}\) is called uniformly continuous on \(d\) if for any \(\varepsilon > 0\), there exists \(\delta > 0\). That makes a big difference. Evaluating whether a function is uniformly continuous requires applying the mathematical definition of uniform continuity,. A. Define Uniform Function.
From www.slideserve.com
PPT Continuous distributions PowerPoint Presentation, free download Define Uniform Function Evaluating whether a function is uniformly continuous requires applying the mathematical definition of uniform continuity,. D \rightarrow \mathbb{r}\) is called uniformly continuous on \(d\) if for any \(\varepsilon > 0\), there exists \(\delta > 0\). That makes a big difference. For $n \in \mathbb{n}$, define the formula, $$f_n(x)= \frac{x}{2n^2x^2+8},\quad x \in [0,1].$$ prove that the sequence $f_n$ converges. But your. Define Uniform Function.
From www.calculussolution.com
Function Limits Define Uniform Function D \rightarrow \mathbb{r}\) is called uniformly continuous on \(d\) if for any \(\varepsilon > 0\), there exists \(\delta > 0\). But your interpretation is rather correct:. That makes a big difference. For $n \in \mathbb{n}$, define the formula, $$f_n(x)= \frac{x}{2n^2x^2+8},\quad x \in [0,1].$$ prove that the sequence $f_n$ converges. First of all, continuity is defined at a point $c$, whereas. Define Uniform Function.
From quantitative-probabilitydistribution.blogspot.com
Uniform Probability Distribution Youtube Research Topics Define Uniform Function For $n \in \mathbb{n}$, define the formula, $$f_n(x)= \frac{x}{2n^2x^2+8},\quad x \in [0,1].$$ prove that the sequence $f_n$ converges. A sequence of functions { fn(x) } with domain d converges uniformly to a function f (x) if given any > 0 there is a. D \rightarrow \mathbb{r}\) is called uniformly continuous on \(d\) if for any \(\varepsilon > 0\), there exists. Define Uniform Function.
From www.slideserve.com
PPT Chapter 1 Examining Distributions PowerPoint Presentation, free Define Uniform Function Evaluating whether a function is uniformly continuous requires applying the mathematical definition of uniform continuity,. A sequence of functions { fn(x) } with domain d converges uniformly to a function f (x) if given any > 0 there is a. First of all, continuity is defined at a point $c$, whereas uniform continuity is defined on a set $a$. For. Define Uniform Function.
From www.youtube.com
Uniform Distribution EXPLAINED with Examples YouTube Define Uniform Function Evaluating whether a function is uniformly continuous requires applying the mathematical definition of uniform continuity,. A sequence of functions { fn(x) } with domain d converges uniformly to a function f (x) if given any > 0 there is a. That makes a big difference. For $n \in \mathbb{n}$, define the formula, $$f_n(x)= \frac{x}{2n^2x^2+8},\quad x \in [0,1].$$ prove that the. Define Uniform Function.
From mungfali.com
Expectation Of Uniform Distribution Define Uniform Function D \rightarrow \mathbb{r}\) is called uniformly continuous on \(d\) if for any \(\varepsilon > 0\), there exists \(\delta > 0\). For $n \in \mathbb{n}$, define the formula, $$f_n(x)= \frac{x}{2n^2x^2+8},\quad x \in [0,1].$$ prove that the sequence $f_n$ converges. First of all, continuity is defined at a point $c$, whereas uniform continuity is defined on a set $a$. A sequence of. Define Uniform Function.
From www.youtube.com
06 Every uniform continuous function is continuous in that interval Define Uniform Function First of all, continuity is defined at a point $c$, whereas uniform continuity is defined on a set $a$. A sequence of functions { fn(x) } with domain d converges uniformly to a function f (x) if given any > 0 there is a. D \rightarrow \mathbb{r}\) is called uniformly continuous on \(d\) if for any \(\varepsilon > 0\), there. Define Uniform Function.
From www.vrogue.co
Uniform Distribution Definition How It Works And Exam vrogue.co Define Uniform Function Evaluating whether a function is uniformly continuous requires applying the mathematical definition of uniform continuity,. D \rightarrow \mathbb{r}\) is called uniformly continuous on \(d\) if for any \(\varepsilon > 0\), there exists \(\delta > 0\). But your interpretation is rather correct:. For $n \in \mathbb{n}$, define the formula, $$f_n(x)= \frac{x}{2n^2x^2+8},\quad x \in [0,1].$$ prove that the sequence $f_n$ converges. First. Define Uniform Function.