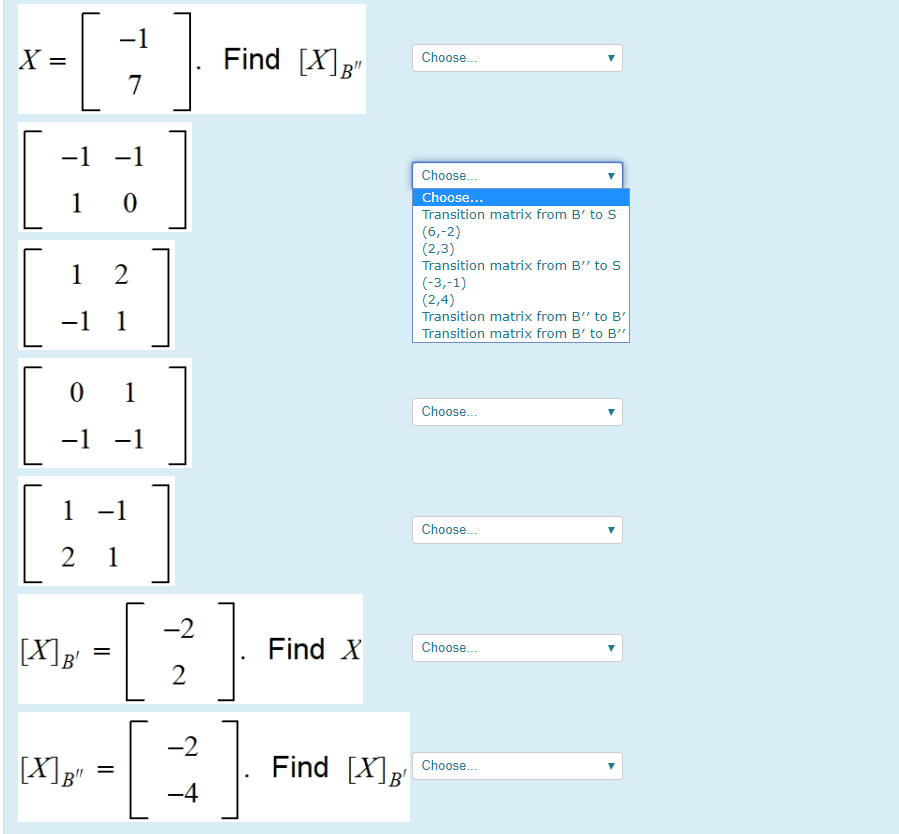
Standard Basis In R2 . a natural basis of r2 is given by the vectors [1; $(a + bi, c + di)$)? In particular, \(\mathbb{r}^n \) has dimension \(n\). Is called the standard basis of the. This is sometimes known as the standard basis. the standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. the standard basis is the unique basis on $\mathbb r^n$ for which these two kinds of coordinates are the same. form a basis for \(\mathbb{r}^n \). a standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a. | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. I know the standard for $\bbb. The collection {i, j} is a basis for r 2, since it spans r 2 and the vectors i and j are linearly independent (because neither is a multiple of.
from www.chegg.com
In particular, \(\mathbb{r}^n \) has dimension \(n\). I know the standard for $\bbb. The collection {i, j} is a basis for r 2, since it spans r 2 and the vectors i and j are linearly independent (because neither is a multiple of. a natural basis of r2 is given by the vectors [1; the standard basis is the unique basis on $\mathbb r^n$ for which these two kinds of coordinates are the same. $(a + bi, c + di)$)? a standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a. the standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. This is sometimes known as the standard basis. | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2.
Solved Consider the following three bases for R2 standard
Standard Basis In R2 the standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. In particular, \(\mathbb{r}^n \) has dimension \(n\). a natural basis of r2 is given by the vectors [1; This is sometimes known as the standard basis. | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. a standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a. form a basis for \(\mathbb{r}^n \). the standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. the standard basis is the unique basis on $\mathbb r^n$ for which these two kinds of coordinates are the same. Is called the standard basis of the. The collection {i, j} is a basis for r 2, since it spans r 2 and the vectors i and j are linearly independent (because neither is a multiple of. $(a + bi, c + di)$)? I know the standard for $\bbb.
From www.youtube.com
Linear Algebra Finding a basis for a line in R^2 YouTube Standard Basis In R2 a natural basis of r2 is given by the vectors [1; the standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. $(a + bi, c + di)$)? Is called the standard basis of the. the standard basis is the unique basis on $\mathbb r^n$ for which these two kinds of. Standard Basis In R2.
From oneclass.com
OneClass solve Let B be the standard basis for R2 and let C be the Standard Basis In R2 In particular, \(\mathbb{r}^n \) has dimension \(n\). This is sometimes known as the standard basis. I know the standard for $\bbb. $(a + bi, c + di)$)? the standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. The collection {i, j} is a basis for r 2, since it spans r 2. Standard Basis In R2.
From www.chegg.com
Solved Consider the following three bases for R2. S = Standard Basis In R2 form a basis for \(\mathbb{r}^n \). a standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a. The collection {i, j} is a basis for r 2, since it spans r 2 and the vectors i and j are linearly independent (because neither is a multiple of. . Standard Basis In R2.
From www.chegg.com
Solved (16 points) Consider the linear transform T R2 → R2 Standard Basis In R2 the standard basis is the unique basis on $\mathbb r^n$ for which these two kinds of coordinates are the same. a natural basis of r2 is given by the vectors [1; form a basis for \(\mathbb{r}^n \). I know the standard for $\bbb. a standard basis, also called a natural basis, is a special orthonormal vector. Standard Basis In R2.
From www.slideserve.com
PPT Geometry of R 2 and R 3 PowerPoint Presentation, free download Standard Basis In R2 $(a + bi, c + di)$)? Is called the standard basis of the. In particular, \(\mathbb{r}^n \) has dimension \(n\). the standard basis is the unique basis on $\mathbb r^n$ for which these two kinds of coordinates are the same. | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. I know the standard. Standard Basis In R2.
From www.chegg.com
Solved Let S be the standard ordered basis of R22, that is, Standard Basis In R2 $(a + bi, c + di)$)? a standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a. Is called the standard basis of the. I know the standard for $\bbb. the standard basis is the unique basis on $\mathbb r^n$ for which these two kinds of coordinates are. Standard Basis In R2.
From www.youtube.com
vector spaces /Standard basis / Subspaces of R2, R3 /Translation Standard Basis In R2 form a basis for \(\mathbb{r}^n \). | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. the standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. I know the standard for $\bbb. the standard basis is the unique basis on $\mathbb r^n$ for which these. Standard Basis In R2.
From calcworkshop.com
Basis of Vector Spaces (A Linear Algebra Guide) Standard Basis In R2 I know the standard for $\bbb. This is sometimes known as the standard basis. | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. a natural basis of r2 is given by the vectors [1; the standard basis is the unique basis on $\mathbb r^n$ for which these two kinds of coordinates are. Standard Basis In R2.
From www.chegg.com
Solved Let be the standard basis in R2 and be another Standard Basis In R2 $(a + bi, c + di)$)? | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. form a basis for \(\mathbb{r}^n \). a natural basis of r2 is given by the vectors [1; the standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. a. Standard Basis In R2.
From www.coursehero.com
[Solved] Let S be the standard basis of R2 and B = be another basis. UI Standard Basis In R2 $(a + bi, c + di)$)? a natural basis of r2 is given by the vectors [1; the standard basis is the unique basis on $\mathbb r^n$ for which these two kinds of coordinates are the same. the standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. Is called the. Standard Basis In R2.
From www.numerade.com
Consider the ordered bases B = ((4,3), (1,1)) and C = ((0,2),(3,1 Standard Basis In R2 The collection {i, j} is a basis for r 2, since it spans r 2 and the vectors i and j are linearly independent (because neither is a multiple of. the standard basis is the unique basis on $\mathbb r^n$ for which these two kinds of coordinates are the same. Is called the standard basis of the. I know. Standard Basis In R2.
From www.chegg.com
Solved Recall that the standard basis of R2 is E= [e1 e2] Standard Basis In R2 This is sometimes known as the standard basis. form a basis for \(\mathbb{r}^n \). a standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a. $(a + bi, c + di)$)? I know the standard for $\bbb. In particular, \(\mathbb{r}^n \) has dimension \(n\). the standard basis. Standard Basis In R2.
From www.chegg.com
Solved Let B be the standard basis for R2 and let C be the Standard Basis In R2 The collection {i, j} is a basis for r 2, since it spans r 2 and the vectors i and j are linearly independent (because neither is a multiple of. a natural basis of r2 is given by the vectors [1; the standard basis is the unique basis on $\mathbb r^n$ for which these two kinds of coordinates. Standard Basis In R2.
From www.numerade.com
SOLVED point) The standard basis S = e1, e2 and custom basis B = b1,bz Standard Basis In R2 In particular, \(\mathbb{r}^n \) has dimension \(n\). the standard basis is the unique basis on $\mathbb r^n$ for which these two kinds of coordinates are the same. form a basis for \(\mathbb{r}^n \). $(a + bi, c + di)$)? I know the standard for $\bbb. a standard basis, also called a natural basis, is a special orthonormal. Standard Basis In R2.
From www.chegg.com
Solved 5. (a) Let E be the standard ordered basis for Rand Standard Basis In R2 the standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. Is called the standard basis of the. This is sometimes known as the standard basis. The collection {i, j} is a basis for r 2, since it spans r 2 and the vectors i and j are linearly independent (because neither is. Standard Basis In R2.
From www.chegg.com
Solved Let B be the basis of R2 consisting of the vectors Standard Basis In R2 the standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. This is sometimes known as the standard basis. | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. The collection {i, j} is a basis for r 2, since it spans r 2 and the vectors i. Standard Basis In R2.
From www.chegg.com
Solved Let S = (e1, e2) be the standard ordered basis of R2 Standard Basis In R2 I know the standard for $\bbb. Is called the standard basis of the. | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. the standard basis is the unique basis on $\mathbb r^n$ for which these two kinds of coordinates are the same. a standard basis, also called a natural basis, is a. Standard Basis In R2.
From www.chegg.com
Solved Let S (e,e2) be the standard basis for R2 with Standard Basis In R2 a standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a. I know the standard for $\bbb. | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. form a basis for \(\mathbb{r}^n \). $(a + bi, c + di)$)? This is sometimes known. Standard Basis In R2.
From quizlet.com
Let S be the standard basis for R2, and let B = {v1, v2} be Quizlet Standard Basis In R2 | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. form a basis for \(\mathbb{r}^n \). This is sometimes known as the standard basis. Is called the standard basis of the. In particular, \(\mathbb{r}^n \) has dimension \(n\). the standard basis is the unique basis on $\mathbb r^n$ for which these two kinds. Standard Basis In R2.
From zief0002.github.io
Chapter 16 Basis Vectors and Matrices Matrix Algebra for Educational Standard Basis In R2 the standard basis is the unique basis on $\mathbb r^n$ for which these two kinds of coordinates are the same. $(a + bi, c + di)$)? Is called the standard basis of the. I know the standard for $\bbb. the standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. a. Standard Basis In R2.
From calcworkshop.com
Basis of Vector Spaces (A Linear Algebra Guide) Standard Basis In R2 a standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a. I know the standard for $\bbb. In particular, \(\mathbb{r}^n \) has dimension \(n\). The collection {i, j} is a basis for r 2, since it spans r 2 and the vectors i and j are linearly independent (because. Standard Basis In R2.
From www.chegg.com
Solved Consider the following three bases for R2 standard Standard Basis In R2 a natural basis of r2 is given by the vectors [1; a standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a. The collection {i, j} is a basis for r 2, since it spans r 2 and the vectors i and j are linearly independent (because neither. Standard Basis In R2.
From www.slideshare.net
Subspace, Col Space, basis Standard Basis In R2 | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. Is called the standard basis of the. a standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a. $(a + bi, c + di)$)? a natural basis of r2 is given by the. Standard Basis In R2.
From math.stackexchange.com
linear algebra Why use Transpose notation in standart basis vectors Standard Basis In R2 a natural basis of r2 is given by the vectors [1; form a basis for \(\mathbb{r}^n \). the standard basis is the unique basis on $\mathbb r^n$ for which these two kinds of coordinates are the same. a standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector. Standard Basis In R2.
From brainly.com
Let b be the basis of r2 consisting of the vectors [ 4 ] 2 and [ 2 ] 5 Standard Basis In R2 I know the standard for $\bbb. The collection {i, j} is a basis for r 2, since it spans r 2 and the vectors i and j are linearly independent (because neither is a multiple of. | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. Is called the standard basis of the. the. Standard Basis In R2.
From www.chegg.com
Solved (a) Explain why (i l 2 is a basis for R2, and write Standard Basis In R2 a natural basis of r2 is given by the vectors [1; This is sometimes known as the standard basis. Is called the standard basis of the. I know the standard for $\bbb. form a basis for \(\mathbb{r}^n \). | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. $(a + bi, c +. Standard Basis In R2.
From www.numerade.com
SOLVED Consider the basis B of R2 consisting of the vectors 3 2 6 Standard Basis In R2 the standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. This is sometimes known as the standard basis. The collection {i, j} is a basis for r 2, since it spans r 2 and the vectors i and j are linearly independent (because neither is a multiple of. the standard basis. Standard Basis In R2.
From www.chegg.com
Solved Consider the following three bases for R2 standard Standard Basis In R2 | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. the standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. The collection {i, j} is a basis for r 2, since it spans r 2 and the vectors i and j are linearly independent (because neither is. Standard Basis In R2.
From www.youtube.com
Is { (1,1) , (3,1) } is a basis of R2. Short method to check whether Standard Basis In R2 This is sometimes known as the standard basis. The collection {i, j} is a basis for r 2, since it spans r 2 and the vectors i and j are linearly independent (because neither is a multiple of. $(a + bi, c + di)$)? I know the standard for $\bbb. a standard basis, also called a natural basis, is. Standard Basis In R2.
From www.studyxapp.com
1 point the standard basis s e ez and two custom bases b b b2 and c 1c2 Standard Basis In R2 $(a + bi, c + di)$)? I know the standard for $\bbb. Is called the standard basis of the. form a basis for \(\mathbb{r}^n \). The collection {i, j} is a basis for r 2, since it spans r 2 and the vectors i and j are linearly independent (because neither is a multiple of. This is sometimes known. Standard Basis In R2.
From www.coursehero.com
[Solved] Let S be the standard basis of R2 and B = be another basis. UI Standard Basis In R2 a natural basis of r2 is given by the vectors [1; a standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a. In particular, \(\mathbb{r}^n \) has dimension \(n\). This is sometimes known as the standard basis. Is called the standard basis of the. form a basis. Standard Basis In R2.
From www.chegg.com
Solved (1 point) The standard basis S {ej, e2} and two Standard Basis In R2 In particular, \(\mathbb{r}^n \) has dimension \(n\). I know the standard for $\bbb. a standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a. form a basis for \(\mathbb{r}^n \). Is called the standard basis of the. | | x | | = √x ⋅ x = √(x1)2. Standard Basis In R2.
From www.chegg.com
Solved Bases and Dimension 9. What is the standard basis Standard Basis In R2 a natural basis of r2 is given by the vectors [1; the standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. This is sometimes known as the standard basis. a standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a.. Standard Basis In R2.
From www.youtube.com
12.2 Part 7/8 Quick Introduction to Standard Basis Vector & Unit Standard Basis In R2 Is called the standard basis of the. the standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. a standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a. a natural basis of r2 is given by the vectors [1; The. Standard Basis In R2.
From www.slideserve.com
PPT Quantum Computing PowerPoint Presentation, free download ID6832149 Standard Basis In R2 form a basis for \(\mathbb{r}^n \). This is sometimes known as the standard basis. Is called the standard basis of the. I know the standard for $\bbb. The collection {i, j} is a basis for r 2, since it spans r 2 and the vectors i and j are linearly independent (because neither is a multiple of. the. Standard Basis In R2.