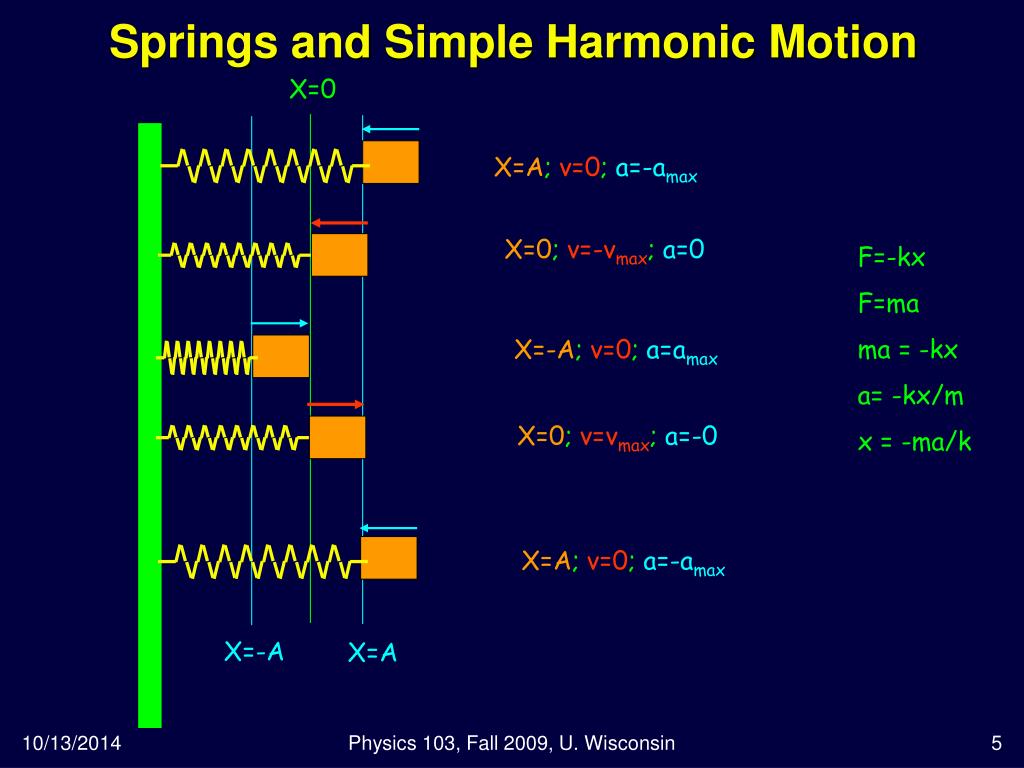
Damped Oscillation Vibration at Joseph Nance blog

Damped Oscillation Vibration. The reduction in amplitude (or energy) of an oscillator is called damping, and the oscillation is said to be damped. The effect of radiation by an oscillating system and of the friction present in the system is that the amplitude of oscillations gradually diminishes with time. In this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to describe this more general case. If the system is very weakly damped, such that \((b / m)^{2}<<4 k / m\), then we can approximate the number of cycles by \[n=[\gamma \tau / 2 \pi] \simeq\left[(k / m)^{1 / 2}(m / \pi b)\right]=\left[\omega_{0}(m / \pi b)\right] \nonumber \] This happens due to resistive forces, such as friction or air resistance, which act in the opposite direction to the motion, or velocity, of an oscillator. A guitar string stops oscillating a few seconds after being plucked. Newton’s second law takes the form f(t) − kx − cdx dt = md2x dt2. Resistive forces acting on an. If a frictional force ( damping ) proportional to the velocity is also present, the harmonic oscillator is described as a damped oscillator. First, you instrument your design by attaching accelerometers to appropriate points. Driven harmonic oscillators are damped oscillators further affected by an externally applied force f (t). You can use the free vibration response to do this, as follows.

The reduction in amplitude (or energy) of an oscillator is called damping, and the oscillation is said to be damped. First, you instrument your design by attaching accelerometers to appropriate points. Driven harmonic oscillators are damped oscillators further affected by an externally applied force f (t). A guitar string stops oscillating a few seconds after being plucked. This happens due to resistive forces, such as friction or air resistance, which act in the opposite direction to the motion, or velocity, of an oscillator. If the system is very weakly damped, such that \((b / m)^{2}<<4 k / m\), then we can approximate the number of cycles by \[n=[\gamma \tau / 2 \pi] \simeq\left[(k / m)^{1 / 2}(m / \pi b)\right]=\left[\omega_{0}(m / \pi b)\right] \nonumber \] If a frictional force ( damping ) proportional to the velocity is also present, the harmonic oscillator is described as a damped oscillator. Newton’s second law takes the form f(t) − kx − cdx dt = md2x dt2. In this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to describe this more general case. The effect of radiation by an oscillating system and of the friction present in the system is that the amplitude of oscillations gradually diminishes with time.

PPT Lecture 25 Chapter 13 Vibrations Simple Harmonic Motion; Damped

Damped Oscillation Vibration The reduction in amplitude (or energy) of an oscillator is called damping, and the oscillation is said to be damped. The effect of radiation by an oscillating system and of the friction present in the system is that the amplitude of oscillations gradually diminishes with time. A guitar string stops oscillating a few seconds after being plucked. Driven harmonic oscillators are damped oscillators further affected by an externally applied force f (t). The reduction in amplitude (or energy) of an oscillator is called damping, and the oscillation is said to be damped. If a frictional force ( damping ) proportional to the velocity is also present, the harmonic oscillator is described as a damped oscillator. First, you instrument your design by attaching accelerometers to appropriate points. This happens due to resistive forces, such as friction or air resistance, which act in the opposite direction to the motion, or velocity, of an oscillator. If the system is very weakly damped, such that \((b / m)^{2}<<4 k / m\), then we can approximate the number of cycles by \[n=[\gamma \tau / 2 \pi] \simeq\left[(k / m)^{1 / 2}(m / \pi b)\right]=\left[\omega_{0}(m / \pi b)\right] \nonumber \] In this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to describe this more general case. Resistive forces acting on an. Newton’s second law takes the form f(t) − kx − cdx dt = md2x dt2. You can use the free vibration response to do this, as follows.