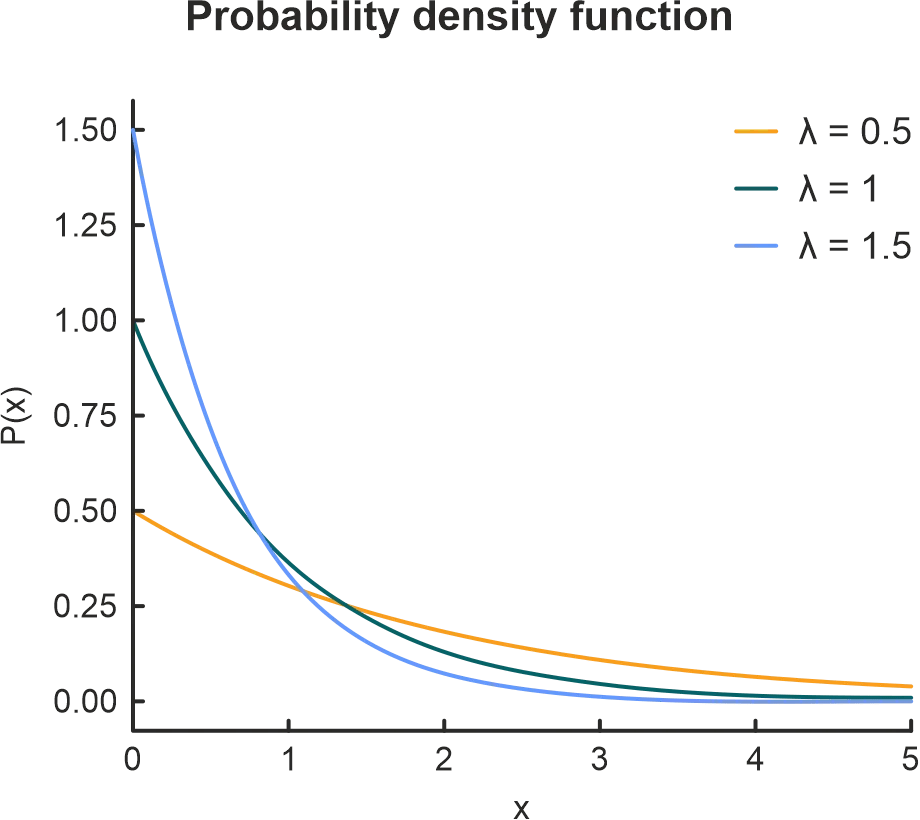
Time Between Events Distribution . Another use of the mass. For example, suppose that an average of 30. A poisson process is a model for a series of discrete event where the average time between events is known, but the exact timing. There is an interesting relationship between the exponential distribution and the poisson distribution. Suppose that the time that elapses between two successive. Conveniently, this data could be fit into a poisson distribution, which can be used. With 1.92 days as average time between events (investments). Exponential distribution doesn't imply that time between events grows exponentially. The time spent waiting between events is often modeled using the exponential distribution. The distribution looks like this: Simply, it is an inverse of poisson. We can use the poisson distribution pmf to find the probability of observing a number of events over an interval generated by a poisson process. The exponential distribution is the time between events in a poisson process. All it tells you is that probability.
from softwaresim.com
Exponential distribution doesn't imply that time between events grows exponentially. A poisson process is a model for a series of discrete event where the average time between events is known, but the exact timing. The distribution looks like this: With 1.92 days as average time between events (investments). The time spent waiting between events is often modeled using the exponential distribution. Suppose that the time that elapses between two successive. The exponential distribution is the time between events in a poisson process. Conveniently, this data could be fit into a poisson distribution, which can be used. All it tells you is that probability. There is an interesting relationship between the exponential distribution and the poisson distribution.
The most important probability distributions for business process
Time Between Events Distribution Simply, it is an inverse of poisson. We can use the poisson distribution pmf to find the probability of observing a number of events over an interval generated by a poisson process. For example, suppose that an average of 30. Simply, it is an inverse of poisson. All it tells you is that probability. A poisson process is a model for a series of discrete event where the average time between events is known, but the exact timing. Suppose that the time that elapses between two successive. There is an interesting relationship between the exponential distribution and the poisson distribution. Another use of the mass. Conveniently, this data could be fit into a poisson distribution, which can be used. The exponential distribution is the time between events in a poisson process. The time spent waiting between events is often modeled using the exponential distribution. With 1.92 days as average time between events (investments). The distribution looks like this: Exponential distribution doesn't imply that time between events grows exponentially.
From www.chegg.com
Solved The binomial distribution consists of the Time Between Events Distribution Simply, it is an inverse of poisson. There is an interesting relationship between the exponential distribution and the poisson distribution. With 1.92 days as average time between events (investments). Suppose that the time that elapses between two successive. All it tells you is that probability. Exponential distribution doesn't imply that time between events grows exponentially. Another use of the mass.. Time Between Events Distribution.
From bookdown.rstudioconnect.com
Chapter 18 Reference Distributions Introduction to Applied Time Between Events Distribution The distribution looks like this: The time spent waiting between events is often modeled using the exponential distribution. A poisson process is a model for a series of discrete event where the average time between events is known, but the exact timing. We can use the poisson distribution pmf to find the probability of observing a number of events over. Time Between Events Distribution.
From www.slideserve.com
PPT Exponential Distribution . PowerPoint Presentation, free download Time Between Events Distribution Simply, it is an inverse of poisson. The distribution looks like this: The time spent waiting between events is often modeled using the exponential distribution. There is an interesting relationship between the exponential distribution and the poisson distribution. Conveniently, this data could be fit into a poisson distribution, which can be used. Another use of the mass. The exponential distribution. Time Between Events Distribution.
From www.studyterrain.com
Application Exponential Distribution In Estimating Arrival Rate And Time Between Events Distribution Another use of the mass. There is an interesting relationship between the exponential distribution and the poisson distribution. Suppose that the time that elapses between two successive. Conveniently, this data could be fit into a poisson distribution, which can be used. The distribution looks like this: The exponential distribution is the time between events in a poisson process. Simply, it. Time Between Events Distribution.
From www.slideserve.com
PPT STAT131 Week 7 L1b Exponential Distribution & relationship to Time Between Events Distribution Another use of the mass. Conveniently, this data could be fit into a poisson distribution, which can be used. There is an interesting relationship between the exponential distribution and the poisson distribution. A poisson process is a model for a series of discrete event where the average time between events is known, but the exact timing. Suppose that the time. Time Between Events Distribution.
From www.linkedin.com
Oji Ndidiamaka Cletus on LinkedIn statistics distribution analysis Time Between Events Distribution All it tells you is that probability. The distribution looks like this: Exponential distribution doesn't imply that time between events grows exponentially. Another use of the mass. There is an interesting relationship between the exponential distribution and the poisson distribution. Suppose that the time that elapses between two successive. We can use the poisson distribution pmf to find the probability. Time Between Events Distribution.
From towardsdatascience.com
Lognormal Distribution A simple explanation by Maja Pavlovic Time Between Events Distribution The exponential distribution is the time between events in a poisson process. The time spent waiting between events is often modeled using the exponential distribution. Simply, it is an inverse of poisson. With 1.92 days as average time between events (investments). Exponential distribution doesn't imply that time between events grows exponentially. A poisson process is a model for a series. Time Between Events Distribution.
From www.chegg.com
Solved The special case of the gamma distribution in which a Time Between Events Distribution The exponential distribution is the time between events in a poisson process. Suppose that the time that elapses between two successive. The time spent waiting between events is often modeled using the exponential distribution. For example, suppose that an average of 30. Simply, it is an inverse of poisson. There is an interesting relationship between the exponential distribution and the. Time Between Events Distribution.
From www.cuemath.com
Exponential Distribution Formula Learn Formula for Exponential Time Between Events Distribution Suppose that the time that elapses between two successive. Conveniently, this data could be fit into a poisson distribution, which can be used. There is an interesting relationship between the exponential distribution and the poisson distribution. Another use of the mass. A poisson process is a model for a series of discrete event where the average time between events is. Time Between Events Distribution.
From www.figpii.com
Distribution Channels Explained (With Examples) FigPii blog Time Between Events Distribution There is an interesting relationship between the exponential distribution and the poisson distribution. For example, suppose that an average of 30. Suppose that the time that elapses between two successive. With 1.92 days as average time between events (investments). The exponential distribution is the time between events in a poisson process. We can use the poisson distribution pmf to find. Time Between Events Distribution.
From www.chegg.com
Solved The special case of the gamma distribution in which a Time Between Events Distribution Suppose that the time that elapses between two successive. For example, suppose that an average of 30. Simply, it is an inverse of poisson. We can use the poisson distribution pmf to find the probability of observing a number of events over an interval generated by a poisson process. The time spent waiting between events is often modeled using the. Time Between Events Distribution.
From bookdown.org
7.1 Exponential distributions An Introduction to Probability and Time Between Events Distribution All it tells you is that probability. The exponential distribution is the time between events in a poisson process. There is an interesting relationship between the exponential distribution and the poisson distribution. Suppose that the time that elapses between two successive. Simply, it is an inverse of poisson. Another use of the mass. Exponential distribution doesn't imply that time between. Time Between Events Distribution.
From www.chegg.com
Solved The special case of the gamma distribution in which α Time Between Events Distribution The exponential distribution is the time between events in a poisson process. Conveniently, this data could be fit into a poisson distribution, which can be used. All it tells you is that probability. A poisson process is a model for a series of discrete event where the average time between events is known, but the exact timing. With 1.92 days. Time Between Events Distribution.
From www.researchgate.net
Rescaled distribution of waiting times. tw is the mean waiting time Time Between Events Distribution The distribution looks like this: The time spent waiting between events is often modeled using the exponential distribution. Exponential distribution doesn't imply that time between events grows exponentially. There is an interesting relationship between the exponential distribution and the poisson distribution. Another use of the mass. We can use the poisson distribution pmf to find the probability of observing a. Time Between Events Distribution.
From www.slideserve.com
PPT Exponential Distribution (Chapter 14) PowerPoint Presentation Time Between Events Distribution For example, suppose that an average of 30. The exponential distribution is the time between events in a poisson process. A poisson process is a model for a series of discrete event where the average time between events is known, but the exact timing. Another use of the mass. The distribution looks like this: The time spent waiting between events. Time Between Events Distribution.
From sherrytowers.com
Poisson, Exponential, and Gamma distributions Polymatheia Time Between Events Distribution There is an interesting relationship between the exponential distribution and the poisson distribution. For example, suppose that an average of 30. Another use of the mass. All it tells you is that probability. A poisson process is a model for a series of discrete event where the average time between events is known, but the exact timing. With 1.92 days. Time Between Events Distribution.
From slidetodoc.com
Uniform Probability Distribution The uniform distribution is a Time Between Events Distribution With 1.92 days as average time between events (investments). Exponential distribution doesn't imply that time between events grows exponentially. The time spent waiting between events is often modeled using the exponential distribution. There is an interesting relationship between the exponential distribution and the poisson distribution. All it tells you is that probability. A poisson process is a model for a. Time Between Events Distribution.
From www.researchgate.net
Observed densities of time between events in the model. Download Time Between Events Distribution Suppose that the time that elapses between two successive. For example, suppose that an average of 30. The time spent waiting between events is often modeled using the exponential distribution. A poisson process is a model for a series of discrete event where the average time between events is known, but the exact timing. We can use the poisson distribution. Time Between Events Distribution.
From quantitative-probabilitydistribution.blogspot.com
Waiting Time Probability Distribution Research Topics Time Between Events Distribution The time spent waiting between events is often modeled using the exponential distribution. We can use the poisson distribution pmf to find the probability of observing a number of events over an interval generated by a poisson process. A poisson process is a model for a series of discrete event where the average time between events is known, but the. Time Between Events Distribution.
From www.chegg.com
Solved Poisson distribution Consider an event with success Time Between Events Distribution A poisson process is a model for a series of discrete event where the average time between events is known, but the exact timing. The distribution looks like this: We can use the poisson distribution pmf to find the probability of observing a number of events over an interval generated by a poisson process. With 1.92 days as average time. Time Between Events Distribution.
From softwaresim.com
The most important probability distributions for business process Time Between Events Distribution The exponential distribution is the time between events in a poisson process. Simply, it is an inverse of poisson. Suppose that the time that elapses between two successive. All it tells you is that probability. Exponential distribution doesn't imply that time between events grows exponentially. A poisson process is a model for a series of discrete event where the average. Time Between Events Distribution.
From www.icecoldcode.com
A Few Common Statistical Distributions Time Between Events Distribution Suppose that the time that elapses between two successive. All it tells you is that probability. A poisson process is a model for a series of discrete event where the average time between events is known, but the exact timing. We can use the poisson distribution pmf to find the probability of observing a number of events over an interval. Time Between Events Distribution.
From www.scribbr.com
The Standard Normal Distribution Examples, Explanations, Uses Time Between Events Distribution Exponential distribution doesn't imply that time between events grows exponentially. With 1.92 days as average time between events (investments). The time spent waiting between events is often modeled using the exponential distribution. The exponential distribution is the time between events in a poisson process. All it tells you is that probability. Simply, it is an inverse of poisson. We can. Time Between Events Distribution.
From www.frontiersin.org
Frontiers Monitoring Betaine Using Interval Time Between Events Time Between Events Distribution Suppose that the time that elapses between two successive. All it tells you is that probability. There is an interesting relationship between the exponential distribution and the poisson distribution. Simply, it is an inverse of poisson. The time spent waiting between events is often modeled using the exponential distribution. With 1.92 days as average time between events (investments). We can. Time Between Events Distribution.
From www.researchgate.net
1 Cumulative distribution and probability density or mass functions of Time Between Events Distribution The time spent waiting between events is often modeled using the exponential distribution. For example, suppose that an average of 30. Another use of the mass. The distribution looks like this: A poisson process is a model for a series of discrete event where the average time between events is known, but the exact timing. We can use the poisson. Time Between Events Distribution.
From www.slideserve.com
PPT Exponential Distribution (Chapter 14) PowerPoint Presentation Time Between Events Distribution The exponential distribution is the time between events in a poisson process. Conveniently, this data could be fit into a poisson distribution, which can be used. Suppose that the time that elapses between two successive. All it tells you is that probability. Another use of the mass. A poisson process is a model for a series of discrete event where. Time Between Events Distribution.
From www.investopedia.com
Lognormal and Normal Distribution Time Between Events Distribution We can use the poisson distribution pmf to find the probability of observing a number of events over an interval generated by a poisson process. Conveniently, this data could be fit into a poisson distribution, which can be used. Another use of the mass. The time spent waiting between events is often modeled using the exponential distribution. All it tells. Time Between Events Distribution.
From www.slideserve.com
PPT The Poisson Process PowerPoint Presentation, free download ID Time Between Events Distribution Simply, it is an inverse of poisson. The exponential distribution is the time between events in a poisson process. For example, suppose that an average of 30. Another use of the mass. The time spent waiting between events is often modeled using the exponential distribution. All it tells you is that probability. The distribution looks like this: With 1.92 days. Time Between Events Distribution.
From byjus.com
Exponential Distribution (Definition, Formula, Mean & Variance Time Between Events Distribution Exponential distribution doesn't imply that time between events grows exponentially. The time spent waiting between events is often modeled using the exponential distribution. There is an interesting relationship between the exponential distribution and the poisson distribution. A poisson process is a model for a series of discrete event where the average time between events is known, but the exact timing.. Time Between Events Distribution.
From predictivehacks.com
Applications of Exponential Distribution Predictive Hacks Time Between Events Distribution Exponential distribution doesn't imply that time between events grows exponentially. Another use of the mass. The time spent waiting between events is often modeled using the exponential distribution. All it tells you is that probability. With 1.92 days as average time between events (investments). Simply, it is an inverse of poisson. For example, suppose that an average of 30. There. Time Between Events Distribution.
From www.researchgate.net
PDF of the interarrival time between events for some earthquake Time Between Events Distribution A poisson process is a model for a series of discrete event where the average time between events is known, but the exact timing. The time spent waiting between events is often modeled using the exponential distribution. All it tells you is that probability. Simply, it is an inverse of poisson. The distribution looks like this: We can use the. Time Between Events Distribution.
From medium.com
Exponential Distribution. Exponential Distribution by Gajendra Medium Time Between Events Distribution A poisson process is a model for a series of discrete event where the average time between events is known, but the exact timing. Exponential distribution doesn't imply that time between events grows exponentially. The exponential distribution is the time between events in a poisson process. There is an interesting relationship between the exponential distribution and the poisson distribution. Simply,. Time Between Events Distribution.
From www.qualitygurus.com
Exponential Distribution Quality Gurus Time Between Events Distribution A poisson process is a model for a series of discrete event where the average time between events is known, but the exact timing. Another use of the mass. We can use the poisson distribution pmf to find the probability of observing a number of events over an interval generated by a poisson process. Simply, it is an inverse of. Time Between Events Distribution.
From www.chegg.com
Solved (At) = The Poisson process is a model for events that Time Between Events Distribution The time spent waiting between events is often modeled using the exponential distribution. Another use of the mass. Suppose that the time that elapses between two successive. The distribution looks like this: Exponential distribution doesn't imply that time between events grows exponentially. Conveniently, this data could be fit into a poisson distribution, which can be used. All it tells you. Time Between Events Distribution.
From www.slideserve.com
PPT Exponential Distribution (Chapter 14) PowerPoint Presentation Time Between Events Distribution Suppose that the time that elapses between two successive. We can use the poisson distribution pmf to find the probability of observing a number of events over an interval generated by a poisson process. With 1.92 days as average time between events (investments). The distribution looks like this: A poisson process is a model for a series of discrete event. Time Between Events Distribution.