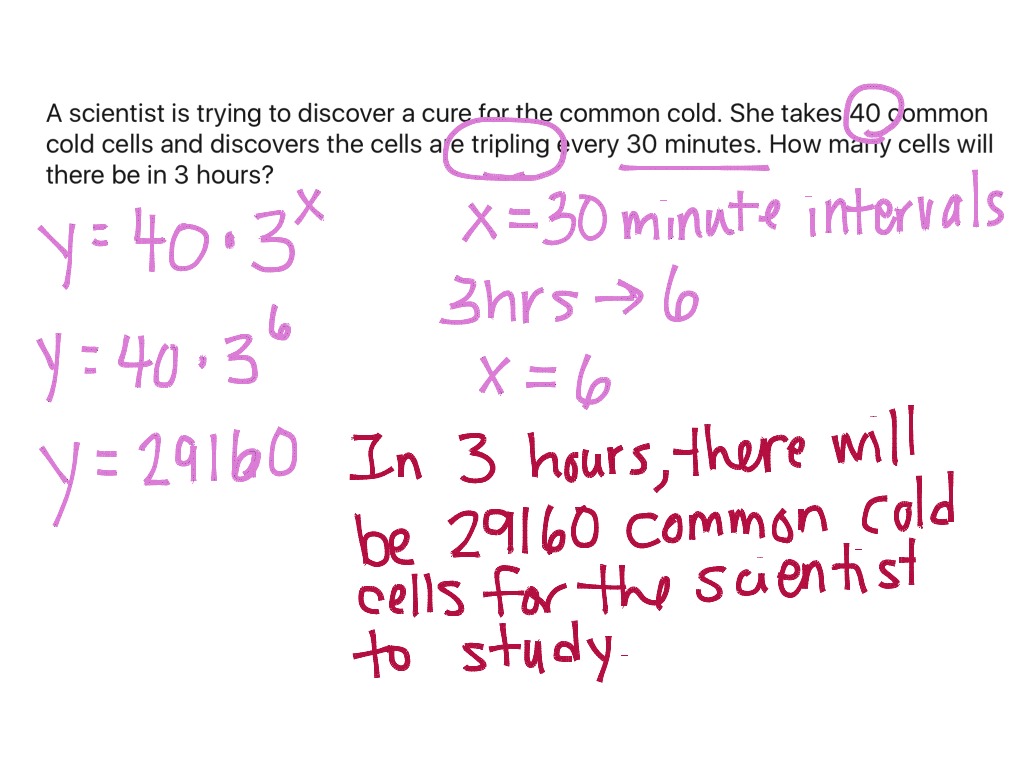Differential Equation Growth And Decay Problems With Solutions . The key model for growth (or decay when c < 0) is dy/dt = c y (t) the next model allows a. This is a key feature of exponential growth. differential equations of growth. set up a differential equation for \(q\). how differential equations arise in scientific problems, how we study their predictions, and what their solutions can tell us about. since the solutions of \(q'=aq\) are exponential functions, we say that a quantity \(q\) that satisfies this equation grows exponentially if \(a > 0\),. that is, the rate of growth is proportional to the current function value. By a solution to a differential. Find the general solution of y2. learn how to solve differential equations using separation of variables and exponential functions. 11.1.2 the solution to a differential equation deþnition 11.2 (solution to a differential equation). Choose your own positive values for \(a\), \(b\), \(k\), and \(q_0=q(0)\).
from www.showme.com
This is a key feature of exponential growth. Choose your own positive values for \(a\), \(b\), \(k\), and \(q_0=q(0)\). set up a differential equation for \(q\). 11.1.2 the solution to a differential equation deþnition 11.2 (solution to a differential equation). since the solutions of \(q'=aq\) are exponential functions, we say that a quantity \(q\) that satisfies this equation grows exponentially if \(a > 0\),. how differential equations arise in scientific problems, how we study their predictions, and what their solutions can tell us about. that is, the rate of growth is proportional to the current function value. Find the general solution of y2. differential equations of growth. learn how to solve differential equations using separation of variables and exponential functions.
ShowMe exponential growth word problems
Differential Equation Growth And Decay Problems With Solutions This is a key feature of exponential growth. 11.1.2 the solution to a differential equation deþnition 11.2 (solution to a differential equation). learn how to solve differential equations using separation of variables and exponential functions. differential equations of growth. This is a key feature of exponential growth. how differential equations arise in scientific problems, how we study their predictions, and what their solutions can tell us about. Choose your own positive values for \(a\), \(b\), \(k\), and \(q_0=q(0)\). The key model for growth (or decay when c < 0) is dy/dt = c y (t) the next model allows a. By a solution to a differential. set up a differential equation for \(q\). that is, the rate of growth is proportional to the current function value. since the solutions of \(q'=aq\) are exponential functions, we say that a quantity \(q\) that satisfies this equation grows exponentially if \(a > 0\),. Find the general solution of y2.
From www.slideserve.com
PPT Section 6.2 Differential Equations Growth and Decay PowerPoint Differential Equation Growth And Decay Problems With Solutions set up a differential equation for \(q\). This is a key feature of exponential growth. Find the general solution of y2. The key model for growth (or decay when c < 0) is dy/dt = c y (t) the next model allows a. since the solutions of \(q'=aq\) are exponential functions, we say that a quantity \(q\) that. Differential Equation Growth And Decay Problems With Solutions.
From www.youtube.com
Solving Differential Equations Growth and Decay YouTube Differential Equation Growth And Decay Problems With Solutions since the solutions of \(q'=aq\) are exponential functions, we say that a quantity \(q\) that satisfies this equation grows exponentially if \(a > 0\),. set up a differential equation for \(q\). This is a key feature of exponential growth. learn how to solve differential equations using separation of variables and exponential functions. By a solution to a. Differential Equation Growth And Decay Problems With Solutions.
From www.youtube.com
Differential Equations Exponential Growth and Decay YouTube Differential Equation Growth And Decay Problems With Solutions set up a differential equation for \(q\). This is a key feature of exponential growth. By a solution to a differential. Choose your own positive values for \(a\), \(b\), \(k\), and \(q_0=q(0)\). learn how to solve differential equations using separation of variables and exponential functions. since the solutions of \(q'=aq\) are exponential functions, we say that a. Differential Equation Growth And Decay Problems With Solutions.
From www.studocu.com
Section 5.3 Differential Equations; Growth and Decay MATH 209 Studocu Differential Equation Growth And Decay Problems With Solutions differential equations of growth. 11.1.2 the solution to a differential equation deþnition 11.2 (solution to a differential equation). The key model for growth (or decay when c < 0) is dy/dt = c y (t) the next model allows a. Find the general solution of y2. that is, the rate of growth is proportional to the current. Differential Equation Growth And Decay Problems With Solutions.
From www.youtube.com
AP Calculus 6.4 Separable Differential Equations, Growth, and Decay Differential Equation Growth And Decay Problems With Solutions differential equations of growth. since the solutions of \(q'=aq\) are exponential functions, we say that a quantity \(q\) that satisfies this equation grows exponentially if \(a > 0\),. This is a key feature of exponential growth. set up a differential equation for \(q\). The key model for growth (or decay when c < 0) is dy/dt =. Differential Equation Growth And Decay Problems With Solutions.
From www.studocu.com
Differential Equation Radioactive Decay Problem SET PROBLEM SETS Differential Equation Growth And Decay Problems With Solutions that is, the rate of growth is proportional to the current function value. Choose your own positive values for \(a\), \(b\), \(k\), and \(q_0=q(0)\). This is a key feature of exponential growth. how differential equations arise in scientific problems, how we study their predictions, and what their solutions can tell us about. Find the general solution of y2.. Differential Equation Growth And Decay Problems With Solutions.
From studylib.net
6.2 Differential Equations Growth and Decay Differential Equation Growth And Decay Problems With Solutions 11.1.2 the solution to a differential equation deþnition 11.2 (solution to a differential equation). This is a key feature of exponential growth. how differential equations arise in scientific problems, how we study their predictions, and what their solutions can tell us about. By a solution to a differential. set up a differential equation for \(q\). differential. Differential Equation Growth And Decay Problems With Solutions.
From www.youtube.com
Differential Equations / Exponential Growth and Decay YouTube Differential Equation Growth And Decay Problems With Solutions 11.1.2 the solution to a differential equation deþnition 11.2 (solution to a differential equation). since the solutions of \(q'=aq\) are exponential functions, we say that a quantity \(q\) that satisfies this equation grows exponentially if \(a > 0\),. Choose your own positive values for \(a\), \(b\), \(k\), and \(q_0=q(0)\). how differential equations arise in scientific problems, how. Differential Equation Growth And Decay Problems With Solutions.
From www.slideserve.com
PPT DIFFERENTIAL EQUATIONS GROWTH AND DECAY PowerPoint Presentation Differential Equation Growth And Decay Problems With Solutions set up a differential equation for \(q\). how differential equations arise in scientific problems, how we study their predictions, and what their solutions can tell us about. differential equations of growth. 11.1.2 the solution to a differential equation deþnition 11.2 (solution to a differential equation). Find the general solution of y2. since the solutions of. Differential Equation Growth And Decay Problems With Solutions.
From www.yumpu.com
Section 6.2 Differential Equations Growth and Decay Differential Differential Equation Growth And Decay Problems With Solutions The key model for growth (or decay when c < 0) is dy/dt = c y (t) the next model allows a. since the solutions of \(q'=aq\) are exponential functions, we say that a quantity \(q\) that satisfies this equation grows exponentially if \(a > 0\),. 11.1.2 the solution to a differential equation deþnition 11.2 (solution to a. Differential Equation Growth And Decay Problems With Solutions.
From www.slideserve.com
PPT Chapter 3 Modeling With FirstOrder Differential Equations Differential Equation Growth And Decay Problems With Solutions The key model for growth (or decay when c < 0) is dy/dt = c y (t) the next model allows a. since the solutions of \(q'=aq\) are exponential functions, we say that a quantity \(q\) that satisfies this equation grows exponentially if \(a > 0\),. set up a differential equation for \(q\). how differential equations arise. Differential Equation Growth And Decay Problems With Solutions.
From www.youtube.com
AP Calculus AB Differential Equations Growth & Decay YouTube Differential Equation Growth And Decay Problems With Solutions set up a differential equation for \(q\). By a solution to a differential. Find the general solution of y2. 11.1.2 the solution to a differential equation deþnition 11.2 (solution to a differential equation). This is a key feature of exponential growth. differential equations of growth. Choose your own positive values for \(a\), \(b\), \(k\), and \(q_0=q(0)\). The. Differential Equation Growth And Decay Problems With Solutions.
From www.showme.com
ShowMe exponential growth word problems Differential Equation Growth And Decay Problems With Solutions This is a key feature of exponential growth. since the solutions of \(q'=aq\) are exponential functions, we say that a quantity \(q\) that satisfies this equation grows exponentially if \(a > 0\),. Find the general solution of y2. Choose your own positive values for \(a\), \(b\), \(k\), and \(q_0=q(0)\). learn how to solve differential equations using separation of. Differential Equation Growth And Decay Problems With Solutions.
From www.youtube.com
6.2 Differential Equations Growth and Decay YouTube Differential Equation Growth And Decay Problems With Solutions Find the general solution of y2. learn how to solve differential equations using separation of variables and exponential functions. differential equations of growth. Choose your own positive values for \(a\), \(b\), \(k\), and \(q_0=q(0)\). 11.1.2 the solution to a differential equation deþnition 11.2 (solution to a differential equation). The key model for growth (or decay when c. Differential Equation Growth And Decay Problems With Solutions.
From www.youtube.com
Differential Equations Exponential Growth and Decay YouTube Differential Equation Growth And Decay Problems With Solutions since the solutions of \(q'=aq\) are exponential functions, we say that a quantity \(q\) that satisfies this equation grows exponentially if \(a > 0\),. set up a differential equation for \(q\). Find the general solution of y2. learn how to solve differential equations using separation of variables and exponential functions. Choose your own positive values for \(a\),. Differential Equation Growth And Decay Problems With Solutions.
From www.youtube.com
Applications of First Order Differential Equations Exponential Decay Differential Equation Growth And Decay Problems With Solutions Choose your own positive values for \(a\), \(b\), \(k\), and \(q_0=q(0)\). 11.1.2 the solution to a differential equation deþnition 11.2 (solution to a differential equation). This is a key feature of exponential growth. how differential equations arise in scientific problems, how we study their predictions, and what their solutions can tell us about. The key model for growth. Differential Equation Growth And Decay Problems With Solutions.
From www.youtube.com
differential equations growth and decay problems YouTube Differential Equation Growth And Decay Problems With Solutions set up a differential equation for \(q\). differential equations of growth. since the solutions of \(q'=aq\) are exponential functions, we say that a quantity \(q\) that satisfies this equation grows exponentially if \(a > 0\),. learn how to solve differential equations using separation of variables and exponential functions. This is a key feature of exponential growth.. Differential Equation Growth And Decay Problems With Solutions.
From www.youtube.com
Differential Equations. Applications of Linear Equations. Growth and Differential Equation Growth And Decay Problems With Solutions 11.1.2 the solution to a differential equation deþnition 11.2 (solution to a differential equation). since the solutions of \(q'=aq\) are exponential functions, we say that a quantity \(q\) that satisfies this equation grows exponentially if \(a > 0\),. This is a key feature of exponential growth. set up a differential equation for \(q\). The key model for. Differential Equation Growth And Decay Problems With Solutions.
From www.youtube.com
6.2 Differential Equations Growth and Decay YouTube Differential Equation Growth And Decay Problems With Solutions differential equations of growth. The key model for growth (or decay when c < 0) is dy/dt = c y (t) the next model allows a. since the solutions of \(q'=aq\) are exponential functions, we say that a quantity \(q\) that satisfies this equation grows exponentially if \(a > 0\),. set up a differential equation for \(q\).. Differential Equation Growth And Decay Problems With Solutions.
From www.youtube.com
Exponential growth and decay in discrete dynamical systems YouTube Differential Equation Growth And Decay Problems With Solutions how differential equations arise in scientific problems, how we study their predictions, and what their solutions can tell us about. The key model for growth (or decay when c < 0) is dy/dt = c y (t) the next model allows a. that is, the rate of growth is proportional to the current function value. learn how. Differential Equation Growth And Decay Problems With Solutions.
From zipworksheet.com
Exponential Function Word Problems Worksheet Differential Equation Growth And Decay Problems With Solutions Find the general solution of y2. since the solutions of \(q'=aq\) are exponential functions, we say that a quantity \(q\) that satisfies this equation grows exponentially if \(a > 0\),. 11.1.2 the solution to a differential equation deþnition 11.2 (solution to a differential equation). differential equations of growth. This is a key feature of exponential growth. . Differential Equation Growth And Decay Problems With Solutions.
From studylib.net
6.2 Differential Equations Growth and Decay Differential Equation Growth And Decay Problems With Solutions learn how to solve differential equations using separation of variables and exponential functions. By a solution to a differential. that is, the rate of growth is proportional to the current function value. set up a differential equation for \(q\). how differential equations arise in scientific problems, how we study their predictions, and what their solutions can. Differential Equation Growth And Decay Problems With Solutions.
From study.com
Exponential Growth & Decay Formula, Function & Graphs Lesson Differential Equation Growth And Decay Problems With Solutions differential equations of growth. 11.1.2 the solution to a differential equation deþnition 11.2 (solution to a differential equation). This is a key feature of exponential growth. The key model for growth (or decay when c < 0) is dy/dt = c y (t) the next model allows a. how differential equations arise in scientific problems, how we. Differential Equation Growth And Decay Problems With Solutions.
From www.youtube.com
How do we solve Differential Equations Growth and Decay MCS22 Lesson Differential Equation Growth And Decay Problems With Solutions This is a key feature of exponential growth. By a solution to a differential. set up a differential equation for \(q\). Choose your own positive values for \(a\), \(b\), \(k\), and \(q_0=q(0)\). that is, the rate of growth is proportional to the current function value. differential equations of growth. Find the general solution of y2. learn. Differential Equation Growth And Decay Problems With Solutions.
From www.slideserve.com
PPT DIFFERENTIAL EQUATIONS GROWTH AND DECAY PowerPoint Presentation Differential Equation Growth And Decay Problems With Solutions since the solutions of \(q'=aq\) are exponential functions, we say that a quantity \(q\) that satisfies this equation grows exponentially if \(a > 0\),. learn how to solve differential equations using separation of variables and exponential functions. This is a key feature of exponential growth. differential equations of growth. how differential equations arise in scientific problems,. Differential Equation Growth And Decay Problems With Solutions.
From tv.apple.com
Differential Equations Growth and Decay Understanding Calculus II Differential Equation Growth And Decay Problems With Solutions that is, the rate of growth is proportional to the current function value. Choose your own positive values for \(a\), \(b\), \(k\), and \(q_0=q(0)\). This is a key feature of exponential growth. 11.1.2 the solution to a differential equation deþnition 11.2 (solution to a differential equation). The key model for growth (or decay when c < 0) is. Differential Equation Growth And Decay Problems With Solutions.
From www.youtube.com
Using Differential Equations to Model Exponential Growth and Decay • [6 Differential Equation Growth And Decay Problems With Solutions The key model for growth (or decay when c < 0) is dy/dt = c y (t) the next model allows a. differential equations of growth. This is a key feature of exponential growth. Find the general solution of y2. that is, the rate of growth is proportional to the current function value. how differential equations arise. Differential Equation Growth And Decay Problems With Solutions.
From www.youtube.com
Differential Equation Growth and Decay Problems (Application) YouTube Differential Equation Growth And Decay Problems With Solutions Choose your own positive values for \(a\), \(b\), \(k\), and \(q_0=q(0)\). that is, the rate of growth is proportional to the current function value. This is a key feature of exponential growth. how differential equations arise in scientific problems, how we study their predictions, and what their solutions can tell us about. set up a differential equation. Differential Equation Growth And Decay Problems With Solutions.
From www.youtube.com
Differential Equations Growth & Decay YouTube Differential Equation Growth And Decay Problems With Solutions 11.1.2 the solution to a differential equation deþnition 11.2 (solution to a differential equation). This is a key feature of exponential growth. since the solutions of \(q'=aq\) are exponential functions, we say that a quantity \(q\) that satisfies this equation grows exponentially if \(a > 0\),. Choose your own positive values for \(a\), \(b\), \(k\), and \(q_0=q(0)\). . Differential Equation Growth And Decay Problems With Solutions.
From www.youtube.com
Differential Equation Growth and Decay Problem(Population Differential Equation Growth And Decay Problems With Solutions since the solutions of \(q'=aq\) are exponential functions, we say that a quantity \(q\) that satisfies this equation grows exponentially if \(a > 0\),. learn how to solve differential equations using separation of variables and exponential functions. 11.1.2 the solution to a differential equation deþnition 11.2 (solution to a differential equation). set up a differential equation. Differential Equation Growth And Decay Problems With Solutions.
From www.youtube.com
6.2 Differential Equations Growth and Decay YouTube Differential Equation Growth And Decay Problems With Solutions By a solution to a differential. Find the general solution of y2. that is, the rate of growth is proportional to the current function value. The key model for growth (or decay when c < 0) is dy/dt = c y (t) the next model allows a. 11.1.2 the solution to a differential equation deþnition 11.2 (solution to. Differential Equation Growth And Decay Problems With Solutions.
From www.slideserve.com
PPT 6.2 Differential Equations Growth and Decay (Part 1) PowerPoint Differential Equation Growth And Decay Problems With Solutions set up a differential equation for \(q\). how differential equations arise in scientific problems, how we study their predictions, and what their solutions can tell us about. differential equations of growth. 11.1.2 the solution to a differential equation deþnition 11.2 (solution to a differential equation). Choose your own positive values for \(a\), \(b\), \(k\), and \(q_0=q(0)\).. Differential Equation Growth And Decay Problems With Solutions.
From www.chegg.com
Solved 1. Differential Equation y ky (Exponential growth or Differential Equation Growth And Decay Problems With Solutions Find the general solution of y2. This is a key feature of exponential growth. how differential equations arise in scientific problems, how we study their predictions, and what their solutions can tell us about. learn how to solve differential equations using separation of variables and exponential functions. The key model for growth (or decay when c < 0). Differential Equation Growth And Decay Problems With Solutions.
From answerlibrarykamryn55.z21.web.core.windows.net
Exponential Growth And Decay Word Problems Worksheet Differential Equation Growth And Decay Problems With Solutions This is a key feature of exponential growth. Find the general solution of y2. how differential equations arise in scientific problems, how we study their predictions, and what their solutions can tell us about. since the solutions of \(q'=aq\) are exponential functions, we say that a quantity \(q\) that satisfies this equation grows exponentially if \(a > 0\),.. Differential Equation Growth And Decay Problems With Solutions.
From www.youtube.com
Applications of First Order Differential Equations Exponential Growth Differential Equation Growth And Decay Problems With Solutions set up a differential equation for \(q\). that is, the rate of growth is proportional to the current function value. since the solutions of \(q'=aq\) are exponential functions, we say that a quantity \(q\) that satisfies this equation grows exponentially if \(a > 0\),. differential equations of growth. Find the general solution of y2. 11.1.2. Differential Equation Growth And Decay Problems With Solutions.