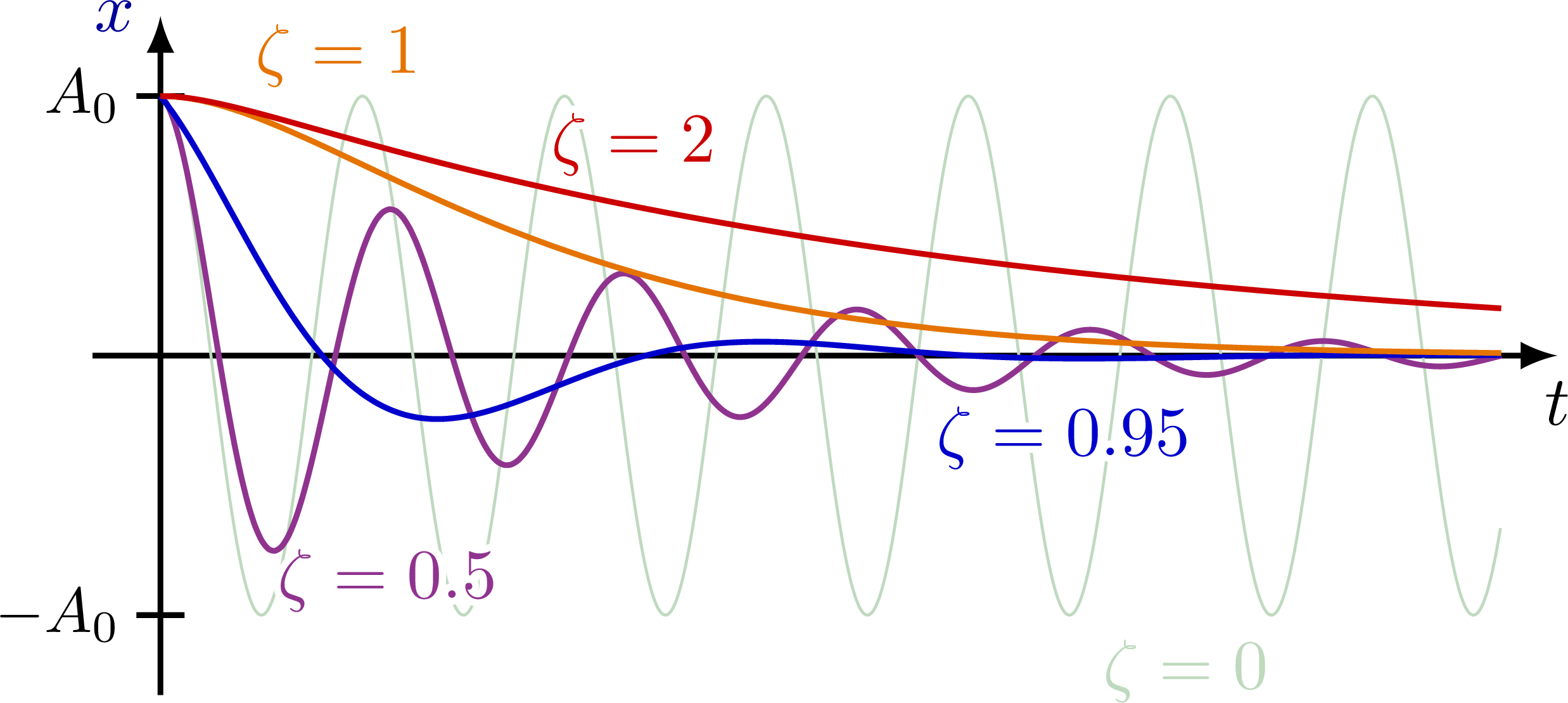
Damped Oscillation Energy . the stored energy at time t = 0 is \[e(t=0)=\frac{1}{2}\left(k+m \alpha^{2}\right) x_{\mathrm{m}}^{2} \nonumber \] the mechanical energy at the conclusion of one cycle, with \(\gamma t=2 \pi\), is \[e(t=t)=\frac{1}{2}\left(k+m This phenomenon is observed in various systems, such as mass oscillating on a spring or shock absorbers in a car. the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2} m v^{2}(t)=\frac{1}{2} m \omega^{2} x_{0}^{2} \sin ^{2}(\omega t+\phi) \nonumber \] the potential energy is given by We have seen that the total energy of a harmonic oscillator remains constant. the mass oscillates around the equilibrium position in a fluid with viscosity but the amplitude decreases for each oscillation. Once started, the oscillations continue forever with a constant amplitude (which is determined from the initial conditions) and a constant frequency (which is determined by the inertial and elastic properties of the system).
from dxoyvbxpm.blob.core.windows.net
the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2} m v^{2}(t)=\frac{1}{2} m \omega^{2} x_{0}^{2} \sin ^{2}(\omega t+\phi) \nonumber \] the potential energy is given by the mass oscillates around the equilibrium position in a fluid with viscosity but the amplitude decreases for each oscillation. This phenomenon is observed in various systems, such as mass oscillating on a spring or shock absorbers in a car. Once started, the oscillations continue forever with a constant amplitude (which is determined from the initial conditions) and a constant frequency (which is determined by the inertial and elastic properties of the system). the stored energy at time t = 0 is \[e(t=0)=\frac{1}{2}\left(k+m \alpha^{2}\right) x_{\mathrm{m}}^{2} \nonumber \] the mechanical energy at the conclusion of one cycle, with \(\gamma t=2 \pi\), is \[e(t=t)=\frac{1}{2}\left(k+m We have seen that the total energy of a harmonic oscillator remains constant.
Damped Oscillation Numericals at Andrew Larson blog
Damped Oscillation Energy We have seen that the total energy of a harmonic oscillator remains constant. the stored energy at time t = 0 is \[e(t=0)=\frac{1}{2}\left(k+m \alpha^{2}\right) x_{\mathrm{m}}^{2} \nonumber \] the mechanical energy at the conclusion of one cycle, with \(\gamma t=2 \pi\), is \[e(t=t)=\frac{1}{2}\left(k+m This phenomenon is observed in various systems, such as mass oscillating on a spring or shock absorbers in a car. We have seen that the total energy of a harmonic oscillator remains constant. the mass oscillates around the equilibrium position in a fluid with viscosity but the amplitude decreases for each oscillation. Once started, the oscillations continue forever with a constant amplitude (which is determined from the initial conditions) and a constant frequency (which is determined by the inertial and elastic properties of the system). the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2} m v^{2}(t)=\frac{1}{2} m \omega^{2} x_{0}^{2} \sin ^{2}(\omega t+\phi) \nonumber \] the potential energy is given by
From studylib.net
Damped Simple Harmonic Motion Damped Oscillation Energy We have seen that the total energy of a harmonic oscillator remains constant. the stored energy at time t = 0 is \[e(t=0)=\frac{1}{2}\left(k+m \alpha^{2}\right) x_{\mathrm{m}}^{2} \nonumber \] the mechanical energy at the conclusion of one cycle, with \(\gamma t=2 \pi\), is \[e(t=t)=\frac{1}{2}\left(k+m the mass oscillates around the equilibrium position in a fluid with viscosity but the amplitude decreases. Damped Oscillation Energy.
From www.slideserve.com
PPT Tutorial 2, Part 2 Calibration of a damped oscillator PowerPoint Damped Oscillation Energy Once started, the oscillations continue forever with a constant amplitude (which is determined from the initial conditions) and a constant frequency (which is determined by the inertial and elastic properties of the system). This phenomenon is observed in various systems, such as mass oscillating on a spring or shock absorbers in a car. the stored energy at time t. Damped Oscillation Energy.
From www.researchgate.net
Graphs of the energy transformations during damped natural oscillations Damped Oscillation Energy the mass oscillates around the equilibrium position in a fluid with viscosity but the amplitude decreases for each oscillation. We have seen that the total energy of a harmonic oscillator remains constant. the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2} m v^{2}(t)=\frac{1}{2} m \omega^{2} x_{0}^{2} \sin ^{2}(\omega t+\phi) \nonumber \] the potential energy is. Damped Oscillation Energy.
From courses.lumenlearning.com
Damped Harmonic Motion Physics Damped Oscillation Energy the stored energy at time t = 0 is \[e(t=0)=\frac{1}{2}\left(k+m \alpha^{2}\right) x_{\mathrm{m}}^{2} \nonumber \] the mechanical energy at the conclusion of one cycle, with \(\gamma t=2 \pi\), is \[e(t=t)=\frac{1}{2}\left(k+m This phenomenon is observed in various systems, such as mass oscillating on a spring or shock absorbers in a car. the mass oscillates around the equilibrium position in a. Damped Oscillation Energy.
From www.slideserve.com
PPT Physics 201 Chapter 14 Oscillations (cont’d) PowerPoint Damped Oscillation Energy Once started, the oscillations continue forever with a constant amplitude (which is determined from the initial conditions) and a constant frequency (which is determined by the inertial and elastic properties of the system). This phenomenon is observed in various systems, such as mass oscillating on a spring or shock absorbers in a car. We have seen that the total energy. Damped Oscillation Energy.
From eduinput.com
Damped OscillationDefinition And Types Damped Oscillation Energy the stored energy at time t = 0 is \[e(t=0)=\frac{1}{2}\left(k+m \alpha^{2}\right) x_{\mathrm{m}}^{2} \nonumber \] the mechanical energy at the conclusion of one cycle, with \(\gamma t=2 \pi\), is \[e(t=t)=\frac{1}{2}\left(k+m Once started, the oscillations continue forever with a constant amplitude (which is determined from the initial conditions) and a constant frequency (which is determined by the inertial and elastic properties. Damped Oscillation Energy.
From animalia-life.club
Damped Harmonic Oscillator Examples Damped Oscillation Energy the mass oscillates around the equilibrium position in a fluid with viscosity but the amplitude decreases for each oscillation. the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2} m v^{2}(t)=\frac{1}{2} m \omega^{2} x_{0}^{2} \sin ^{2}(\omega t+\phi) \nonumber \] the potential energy is given by This phenomenon is observed in various systems, such as mass oscillating. Damped Oscillation Energy.
From www.youtube.com
Damped Oscillation Damped Harmonic Motion Amplitude and Energy of Damped Oscillation Energy This phenomenon is observed in various systems, such as mass oscillating on a spring or shock absorbers in a car. the mass oscillates around the equilibrium position in a fluid with viscosity but the amplitude decreases for each oscillation. Once started, the oscillations continue forever with a constant amplitude (which is determined from the initial conditions) and a constant. Damped Oscillation Energy.
From exomcggho.blob.core.windows.net
Damped Oscillation Shaala at James Bass blog Damped Oscillation Energy This phenomenon is observed in various systems, such as mass oscillating on a spring or shock absorbers in a car. the stored energy at time t = 0 is \[e(t=0)=\frac{1}{2}\left(k+m \alpha^{2}\right) x_{\mathrm{m}}^{2} \nonumber \] the mechanical energy at the conclusion of one cycle, with \(\gamma t=2 \pi\), is \[e(t=t)=\frac{1}{2}\left(k+m the kinetic energy for the driven damped oscillator is. Damped Oscillation Energy.
From energyefficiencyschools.blogspot.com
Energy efficiency in schools Damped oscillation calculator Damped Oscillation Energy This phenomenon is observed in various systems, such as mass oscillating on a spring or shock absorbers in a car. the mass oscillates around the equilibrium position in a fluid with viscosity but the amplitude decreases for each oscillation. the stored energy at time t = 0 is \[e(t=0)=\frac{1}{2}\left(k+m \alpha^{2}\right) x_{\mathrm{m}}^{2} \nonumber \] the mechanical energy at the. Damped Oscillation Energy.
From howwhy.nfshost.com
Damped Oscillation Damped Oscillation Energy the stored energy at time t = 0 is \[e(t=0)=\frac{1}{2}\left(k+m \alpha^{2}\right) x_{\mathrm{m}}^{2} \nonumber \] the mechanical energy at the conclusion of one cycle, with \(\gamma t=2 \pi\), is \[e(t=t)=\frac{1}{2}\left(k+m We have seen that the total energy of a harmonic oscillator remains constant. the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2} m v^{2}(t)=\frac{1}{2} m \omega^{2}. Damped Oscillation Energy.
From www.slideserve.com
PPT PERIODIC MOTION PowerPoint Presentation, free download ID2428605 Damped Oscillation Energy the stored energy at time t = 0 is \[e(t=0)=\frac{1}{2}\left(k+m \alpha^{2}\right) x_{\mathrm{m}}^{2} \nonumber \] the mechanical energy at the conclusion of one cycle, with \(\gamma t=2 \pi\), is \[e(t=t)=\frac{1}{2}\left(k+m the mass oscillates around the equilibrium position in a fluid with viscosity but the amplitude decreases for each oscillation. We have seen that the total energy of a harmonic. Damped Oscillation Energy.
From www.slideserve.com
PPT Waves Oscillations PowerPoint Presentation, free download ID Damped Oscillation Energy We have seen that the total energy of a harmonic oscillator remains constant. the stored energy at time t = 0 is \[e(t=0)=\frac{1}{2}\left(k+m \alpha^{2}\right) x_{\mathrm{m}}^{2} \nonumber \] the mechanical energy at the conclusion of one cycle, with \(\gamma t=2 \pi\), is \[e(t=t)=\frac{1}{2}\left(k+m the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2} m v^{2}(t)=\frac{1}{2} m \omega^{2}. Damped Oscillation Energy.
From www.slideserve.com
PPT Damped Oscillations PowerPoint Presentation, free download ID Damped Oscillation Energy the mass oscillates around the equilibrium position in a fluid with viscosity but the amplitude decreases for each oscillation. Once started, the oscillations continue forever with a constant amplitude (which is determined from the initial conditions) and a constant frequency (which is determined by the inertial and elastic properties of the system). the kinetic energy for the driven. Damped Oscillation Energy.
From www.slideserve.com
PPT Physics 201 Chapter 14 Oscillations (cont’d) PowerPoint Damped Oscillation Energy the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2} m v^{2}(t)=\frac{1}{2} m \omega^{2} x_{0}^{2} \sin ^{2}(\omega t+\phi) \nonumber \] the potential energy is given by We have seen that the total energy of a harmonic oscillator remains constant. Once started, the oscillations continue forever with a constant amplitude (which is determined from the initial conditions) and. Damped Oscillation Energy.
From www.slideserve.com
PPT Lesson 1 Oscillations PowerPoint Presentation, free download Damped Oscillation Energy the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2} m v^{2}(t)=\frac{1}{2} m \omega^{2} x_{0}^{2} \sin ^{2}(\omega t+\phi) \nonumber \] the potential energy is given by Once started, the oscillations continue forever with a constant amplitude (which is determined from the initial conditions) and a constant frequency (which is determined by the inertial and elastic properties of. Damped Oscillation Energy.
From whatsinsight.org
Damped Oscillation Formula and Daily Life Examples What's Insight Damped Oscillation Energy We have seen that the total energy of a harmonic oscillator remains constant. This phenomenon is observed in various systems, such as mass oscillating on a spring or shock absorbers in a car. the mass oscillates around the equilibrium position in a fluid with viscosity but the amplitude decreases for each oscillation. the kinetic energy for the driven. Damped Oscillation Energy.
From www.slideserve.com
PPT Chapter 13 Oscillatory Motions PowerPoint Presentation, free Damped Oscillation Energy We have seen that the total energy of a harmonic oscillator remains constant. the mass oscillates around the equilibrium position in a fluid with viscosity but the amplitude decreases for each oscillation. the stored energy at time t = 0 is \[e(t=0)=\frac{1}{2}\left(k+m \alpha^{2}\right) x_{\mathrm{m}}^{2} \nonumber \] the mechanical energy at the conclusion of one cycle, with \(\gamma t=2. Damped Oscillation Energy.
From dxoyvbxpm.blob.core.windows.net
Damped Oscillation Numericals at Andrew Larson blog Damped Oscillation Energy This phenomenon is observed in various systems, such as mass oscillating on a spring or shock absorbers in a car. the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2} m v^{2}(t)=\frac{1}{2} m \omega^{2} x_{0}^{2} \sin ^{2}(\omega t+\phi) \nonumber \] the potential energy is given by the mass oscillates around the equilibrium position in a fluid. Damped Oscillation Energy.
From www.slideserve.com
PPT Damped Oscillations PowerPoint Presentation, free download ID Damped Oscillation Energy the stored energy at time t = 0 is \[e(t=0)=\frac{1}{2}\left(k+m \alpha^{2}\right) x_{\mathrm{m}}^{2} \nonumber \] the mechanical energy at the conclusion of one cycle, with \(\gamma t=2 \pi\), is \[e(t=t)=\frac{1}{2}\left(k+m Once started, the oscillations continue forever with a constant amplitude (which is determined from the initial conditions) and a constant frequency (which is determined by the inertial and elastic properties. Damped Oscillation Energy.
From www.slideserve.com
PPT Chapter 14 Oscillations PowerPoint Presentation, free download Damped Oscillation Energy the mass oscillates around the equilibrium position in a fluid with viscosity but the amplitude decreases for each oscillation. We have seen that the total energy of a harmonic oscillator remains constant. the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2} m v^{2}(t)=\frac{1}{2} m \omega^{2} x_{0}^{2} \sin ^{2}(\omega t+\phi) \nonumber \] the potential energy is. Damped Oscillation Energy.
From courses.physics.illinois.edu
Physics 111 Lab 8 Damped Oscillation Energy the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2} m v^{2}(t)=\frac{1}{2} m \omega^{2} x_{0}^{2} \sin ^{2}(\omega t+\phi) \nonumber \] the potential energy is given by We have seen that the total energy of a harmonic oscillator remains constant. This phenomenon is observed in various systems, such as mass oscillating on a spring or shock absorbers in. Damped Oscillation Energy.
From www.youtube.com
Damped Oscillations YouTube Damped Oscillation Energy Once started, the oscillations continue forever with a constant amplitude (which is determined from the initial conditions) and a constant frequency (which is determined by the inertial and elastic properties of the system). the mass oscillates around the equilibrium position in a fluid with viscosity but the amplitude decreases for each oscillation. We have seen that the total energy. Damped Oscillation Energy.
From dxoyvbxpm.blob.core.windows.net
Damped Oscillation Numericals at Andrew Larson blog Damped Oscillation Energy the mass oscillates around the equilibrium position in a fluid with viscosity but the amplitude decreases for each oscillation. Once started, the oscillations continue forever with a constant amplitude (which is determined from the initial conditions) and a constant frequency (which is determined by the inertial and elastic properties of the system). This phenomenon is observed in various systems,. Damped Oscillation Energy.
From www.youtube.com
Damped Oscillations YouTube Damped Oscillation Energy This phenomenon is observed in various systems, such as mass oscillating on a spring or shock absorbers in a car. Once started, the oscillations continue forever with a constant amplitude (which is determined from the initial conditions) and a constant frequency (which is determined by the inertial and elastic properties of the system). the stored energy at time t. Damped Oscillation Energy.
From exounhfkb.blob.core.windows.net
Damped Harmonic Oscillator Equation at Hannah Sullivan blog Damped Oscillation Energy We have seen that the total energy of a harmonic oscillator remains constant. the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2} m v^{2}(t)=\frac{1}{2} m \omega^{2} x_{0}^{2} \sin ^{2}(\omega t+\phi) \nonumber \] the potential energy is given by the stored energy at time t = 0 is \[e(t=0)=\frac{1}{2}\left(k+m \alpha^{2}\right) x_{\mathrm{m}}^{2} \nonumber \] the mechanical energy. Damped Oscillation Energy.
From www.nagwa.com
Video Damped Oscillations Nagwa Damped Oscillation Energy the mass oscillates around the equilibrium position in a fluid with viscosity but the amplitude decreases for each oscillation. the stored energy at time t = 0 is \[e(t=0)=\frac{1}{2}\left(k+m \alpha^{2}\right) x_{\mathrm{m}}^{2} \nonumber \] the mechanical energy at the conclusion of one cycle, with \(\gamma t=2 \pi\), is \[e(t=t)=\frac{1}{2}\left(k+m the kinetic energy for the driven damped oscillator is. Damped Oscillation Energy.
From www.slideserve.com
PPT Physics 121 Electricity & Lecture 13 EM Damped Oscillation Energy This phenomenon is observed in various systems, such as mass oscillating on a spring or shock absorbers in a car. the mass oscillates around the equilibrium position in a fluid with viscosity but the amplitude decreases for each oscillation. the stored energy at time t = 0 is \[e(t=0)=\frac{1}{2}\left(k+m \alpha^{2}\right) x_{\mathrm{m}}^{2} \nonumber \] the mechanical energy at the. Damped Oscillation Energy.
From physics.icalculator.com
What is a RLC Circuit? Damped Oscillations in a RLC Circuit iCalcula Damped Oscillation Energy Once started, the oscillations continue forever with a constant amplitude (which is determined from the initial conditions) and a constant frequency (which is determined by the inertial and elastic properties of the system). the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2} m v^{2}(t)=\frac{1}{2} m \omega^{2} x_{0}^{2} \sin ^{2}(\omega t+\phi) \nonumber \] the potential energy is. Damped Oscillation Energy.
From dxoyvbxpm.blob.core.windows.net
Damped Oscillation Numericals at Andrew Larson blog Damped Oscillation Energy We have seen that the total energy of a harmonic oscillator remains constant. the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2} m v^{2}(t)=\frac{1}{2} m \omega^{2} x_{0}^{2} \sin ^{2}(\omega t+\phi) \nonumber \] the potential energy is given by This phenomenon is observed in various systems, such as mass oscillating on a spring or shock absorbers in. Damped Oscillation Energy.
From www.studypool.com
SOLUTION Free and damped oscillation Studypool Damped Oscillation Energy the stored energy at time t = 0 is \[e(t=0)=\frac{1}{2}\left(k+m \alpha^{2}\right) x_{\mathrm{m}}^{2} \nonumber \] the mechanical energy at the conclusion of one cycle, with \(\gamma t=2 \pi\), is \[e(t=t)=\frac{1}{2}\left(k+m Once started, the oscillations continue forever with a constant amplitude (which is determined from the initial conditions) and a constant frequency (which is determined by the inertial and elastic properties. Damped Oscillation Energy.
From www.slideserve.com
PPT Waves Oscillations PowerPoint Presentation, free download ID Damped Oscillation Energy the mass oscillates around the equilibrium position in a fluid with viscosity but the amplitude decreases for each oscillation. This phenomenon is observed in various systems, such as mass oscillating on a spring or shock absorbers in a car. the stored energy at time t = 0 is \[e(t=0)=\frac{1}{2}\left(k+m \alpha^{2}\right) x_{\mathrm{m}}^{2} \nonumber \] the mechanical energy at the. Damped Oscillation Energy.
From www.slideserve.com
PPT Physics 201 Chapter 14 Oscillations (cont’d) PowerPoint Damped Oscillation Energy We have seen that the total energy of a harmonic oscillator remains constant. the mass oscillates around the equilibrium position in a fluid with viscosity but the amplitude decreases for each oscillation. the stored energy at time t = 0 is \[e(t=0)=\frac{1}{2}\left(k+m \alpha^{2}\right) x_{\mathrm{m}}^{2} \nonumber \] the mechanical energy at the conclusion of one cycle, with \(\gamma t=2. Damped Oscillation Energy.
From www.youtube.com
DAMPED OSCILLATION PHYSICS YouTube Damped Oscillation Energy the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2} m v^{2}(t)=\frac{1}{2} m \omega^{2} x_{0}^{2} \sin ^{2}(\omega t+\phi) \nonumber \] the potential energy is given by Once started, the oscillations continue forever with a constant amplitude (which is determined from the initial conditions) and a constant frequency (which is determined by the inertial and elastic properties of. Damped Oscillation Energy.
From www.slideserve.com
PPT Damped Oscillations PowerPoint Presentation, free download ID Damped Oscillation Energy the mass oscillates around the equilibrium position in a fluid with viscosity but the amplitude decreases for each oscillation. We have seen that the total energy of a harmonic oscillator remains constant. the stored energy at time t = 0 is \[e(t=0)=\frac{1}{2}\left(k+m \alpha^{2}\right) x_{\mathrm{m}}^{2} \nonumber \] the mechanical energy at the conclusion of one cycle, with \(\gamma t=2. Damped Oscillation Energy.