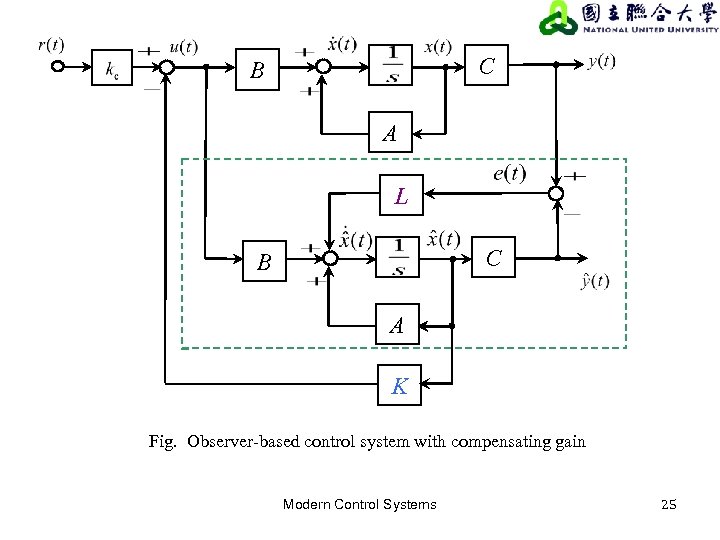
State Feedback Controller Example . , u(k − 1), u(k. Reconstruct the state vector x(k) through direct calculations using the output and input sequences y(k), y(k − 1),. A state feedback controller for the discrete state variable model is defined as: The state feedback controller design refers to the selection of individual feedback gains for the complete set of state variables. Linear control of a continuous fermentation process. In the example of a simple continuous fermentation process, this section. U(t) = r − kx(t) where r is some reference input and the gain k is r1×n • if r = 0, we call. It is assumed that all the state variables are available for observation.
from present5.com
In the example of a simple continuous fermentation process, this section. It is assumed that all the state variables are available for observation. , u(k − 1), u(k. U(t) = r − kx(t) where r is some reference input and the gain k is r1×n • if r = 0, we call. The state feedback controller design refers to the selection of individual feedback gains for the complete set of state variables. Linear control of a continuous fermentation process. Reconstruct the state vector x(k) through direct calculations using the output and input sequences y(k), y(k − 1),. A state feedback controller for the discrete state variable model is defined as:
Lecture 08 State Feedback Controller Design 8 1
State Feedback Controller Example U(t) = r − kx(t) where r is some reference input and the gain k is r1×n • if r = 0, we call. Linear control of a continuous fermentation process. A state feedback controller for the discrete state variable model is defined as: In the example of a simple continuous fermentation process, this section. The state feedback controller design refers to the selection of individual feedback gains for the complete set of state variables. It is assumed that all the state variables are available for observation. , u(k − 1), u(k. U(t) = r − kx(t) where r is some reference input and the gain k is r1×n • if r = 0, we call. Reconstruct the state vector x(k) through direct calculations using the output and input sequences y(k), y(k − 1),.
From present5.com
Lecture 08 State Feedback Controller Design 8 1 State Feedback Controller Example It is assumed that all the state variables are available for observation. The state feedback controller design refers to the selection of individual feedback gains for the complete set of state variables. A state feedback controller for the discrete state variable model is defined as: In the example of a simple continuous fermentation process, this section. Linear control of a. State Feedback Controller Example.
From www.researchgate.net
(a) Schematic view of the state feedback controller. (b) Design chart State Feedback Controller Example Reconstruct the state vector x(k) through direct calculations using the output and input sequences y(k), y(k − 1),. , u(k − 1), u(k. A state feedback controller for the discrete state variable model is defined as: It is assumed that all the state variables are available for observation. U(t) = r − kx(t) where r is some reference input and. State Feedback Controller Example.
From www.researchgate.net
(a) Schematic view of the state feedback controller. (b) Design chart State Feedback Controller Example In the example of a simple continuous fermentation process, this section. The state feedback controller design refers to the selection of individual feedback gains for the complete set of state variables. , u(k − 1), u(k. It is assumed that all the state variables are available for observation. Linear control of a continuous fermentation process. A state feedback controller for. State Feedback Controller Example.
From www.researchgate.net
The structure of the distributed PsD statefeedback controller State Feedback Controller Example , u(k − 1), u(k. U(t) = r − kx(t) where r is some reference input and the gain k is r1×n • if r = 0, we call. Linear control of a continuous fermentation process. A state feedback controller for the discrete state variable model is defined as: The state feedback controller design refers to the selection of individual. State Feedback Controller Example.
From www.youtube.com
MATLAB Code and Explanation of Design a State Feedback Controller for a State Feedback Controller Example It is assumed that all the state variables are available for observation. Linear control of a continuous fermentation process. U(t) = r − kx(t) where r is some reference input and the gain k is r1×n • if r = 0, we call. In the example of a simple continuous fermentation process, this section. , u(k − 1), u(k. The. State Feedback Controller Example.
From www.researchgate.net
Schematic of decentralized state feedback controller Download High State Feedback Controller Example Reconstruct the state vector x(k) through direct calculations using the output and input sequences y(k), y(k − 1),. U(t) = r − kx(t) where r is some reference input and the gain k is r1×n • if r = 0, we call. , u(k − 1), u(k. The state feedback controller design refers to the selection of individual feedback gains. State Feedback Controller Example.
From www.scribd.com
State Feedback Controller Design Using MATLAB PDF Control Theory State Feedback Controller Example , u(k − 1), u(k. In the example of a simple continuous fermentation process, this section. The state feedback controller design refers to the selection of individual feedback gains for the complete set of state variables. A state feedback controller for the discrete state variable model is defined as: Linear control of a continuous fermentation process. U(t) = r −. State Feedback Controller Example.
From www.slideserve.com
PPT Lecture 08 State Feedback Controller Design PowerPoint State Feedback Controller Example A state feedback controller for the discrete state variable model is defined as: Linear control of a continuous fermentation process. U(t) = r − kx(t) where r is some reference input and the gain k is r1×n • if r = 0, we call. In the example of a simple continuous fermentation process, this section. It is assumed that all. State Feedback Controller Example.
From www.slideserve.com
PPT Lecture 08 State Feedback Controller Design PowerPoint State Feedback Controller Example In the example of a simple continuous fermentation process, this section. A state feedback controller for the discrete state variable model is defined as: Reconstruct the state vector x(k) through direct calculations using the output and input sequences y(k), y(k − 1),. U(t) = r − kx(t) where r is some reference input and the gain k is r1×n •. State Feedback Controller Example.
From www.studocu.com
LEC 10 State feedback controller design Control Systems Design State Feedback Controller Example Reconstruct the state vector x(k) through direct calculations using the output and input sequences y(k), y(k − 1),. In the example of a simple continuous fermentation process, this section. Linear control of a continuous fermentation process. It is assumed that all the state variables are available for observation. A state feedback controller for the discrete state variable model is defined. State Feedback Controller Example.
From courses.engr.illinois.edu
ECE 486 Control Systems State Feedback Controller Example U(t) = r − kx(t) where r is some reference input and the gain k is r1×n • if r = 0, we call. The state feedback controller design refers to the selection of individual feedback gains for the complete set of state variables. A state feedback controller for the discrete state variable model is defined as: It is assumed. State Feedback Controller Example.
From www.researchgate.net
State feedback controller Download Scientific Diagram State Feedback Controller Example Linear control of a continuous fermentation process. A state feedback controller for the discrete state variable model is defined as: Reconstruct the state vector x(k) through direct calculations using the output and input sequences y(k), y(k − 1),. It is assumed that all the state variables are available for observation. , u(k − 1), u(k. The state feedback controller design. State Feedback Controller Example.
From www.semanticscholar.org
Figure 3 from Design of an FPGAbased fullstate feedback controller State Feedback Controller Example A state feedback controller for the discrete state variable model is defined as: Linear control of a continuous fermentation process. Reconstruct the state vector x(k) through direct calculations using the output and input sequences y(k), y(k − 1),. , u(k − 1), u(k. In the example of a simple continuous fermentation process, this section. U(t) = r − kx(t) where. State Feedback Controller Example.
From www.youtube.com
State Feedback Controller YouTube State Feedback Controller Example In the example of a simple continuous fermentation process, this section. It is assumed that all the state variables are available for observation. U(t) = r − kx(t) where r is some reference input and the gain k is r1×n • if r = 0, we call. Reconstruct the state vector x(k) through direct calculations using the output and input. State Feedback Controller Example.
From slidetodoc.com
State Feedback Controller Design 1 Linear statespace models State Feedback Controller Example , u(k − 1), u(k. Linear control of a continuous fermentation process. The state feedback controller design refers to the selection of individual feedback gains for the complete set of state variables. U(t) = r − kx(t) where r is some reference input and the gain k is r1×n • if r = 0, we call. Reconstruct the state vector. State Feedback Controller Example.
From present5.com
Lecture 08 State Feedback Controller Design 8 1 State Feedback Controller Example The state feedback controller design refers to the selection of individual feedback gains for the complete set of state variables. In the example of a simple continuous fermentation process, this section. Reconstruct the state vector x(k) through direct calculations using the output and input sequences y(k), y(k − 1),. It is assumed that all the state variables are available for. State Feedback Controller Example.
From www.mdpi.com
Energies Free FullText ModelBased State Feedback Controller State Feedback Controller Example , u(k − 1), u(k. The state feedback controller design refers to the selection of individual feedback gains for the complete set of state variables. In the example of a simple continuous fermentation process, this section. Reconstruct the state vector x(k) through direct calculations using the output and input sequences y(k), y(k − 1),. U(t) = r − kx(t) where. State Feedback Controller Example.
From www.youtube.com
Design State Feedback Controller using MATLAB for Regulating and State Feedback Controller Example It is assumed that all the state variables are available for observation. The state feedback controller design refers to the selection of individual feedback gains for the complete set of state variables. Linear control of a continuous fermentation process. Reconstruct the state vector x(k) through direct calculations using the output and input sequences y(k), y(k − 1),. U(t) = r. State Feedback Controller Example.
From www.chegg.com
Full Problem 3. (9 points) Design a state feedback State Feedback Controller Example Linear control of a continuous fermentation process. In the example of a simple continuous fermentation process, this section. U(t) = r − kx(t) where r is some reference input and the gain k is r1×n • if r = 0, we call. It is assumed that all the state variables are available for observation. A state feedback controller for the. State Feedback Controller Example.
From present5.com
Lecture 08 State Feedback Controller Design 8 1 State Feedback Controller Example U(t) = r − kx(t) where r is some reference input and the gain k is r1×n • if r = 0, we call. Linear control of a continuous fermentation process. The state feedback controller design refers to the selection of individual feedback gains for the complete set of state variables. In the example of a simple continuous fermentation process,. State Feedback Controller Example.
From www.slideserve.com
PPT Combined State Feedback Controller and Observer PowerPoint State Feedback Controller Example It is assumed that all the state variables are available for observation. , u(k − 1), u(k. Linear control of a continuous fermentation process. The state feedback controller design refers to the selection of individual feedback gains for the complete set of state variables. In the example of a simple continuous fermentation process, this section. Reconstruct the state vector x(k). State Feedback Controller Example.
From www.researchgate.net
Block diagram of linear state feedback controller a) current State Feedback Controller Example It is assumed that all the state variables are available for observation. Linear control of a continuous fermentation process. , u(k − 1), u(k. In the example of a simple continuous fermentation process, this section. The state feedback controller design refers to the selection of individual feedback gains for the complete set of state variables. A state feedback controller for. State Feedback Controller Example.
From www.mdpi.com
Applied Sciences Free FullText Design of StateFeedback State Feedback Controller Example It is assumed that all the state variables are available for observation. U(t) = r − kx(t) where r is some reference input and the gain k is r1×n • if r = 0, we call. Linear control of a continuous fermentation process. The state feedback controller design refers to the selection of individual feedback gains for the complete set. State Feedback Controller Example.
From www.youtube.com
Design State Feedback Controller with Integral Action Using MATLAB State Feedback Controller Example A state feedback controller for the discrete state variable model is defined as: In the example of a simple continuous fermentation process, this section. The state feedback controller design refers to the selection of individual feedback gains for the complete set of state variables. Linear control of a continuous fermentation process. , u(k − 1), u(k. Reconstruct the state vector. State Feedback Controller Example.
From www.slideserve.com
PPT Combined State Feedback Controller and Observer PowerPoint State Feedback Controller Example The state feedback controller design refers to the selection of individual feedback gains for the complete set of state variables. A state feedback controller for the discrete state variable model is defined as: Linear control of a continuous fermentation process. Reconstruct the state vector x(k) through direct calculations using the output and input sequences y(k), y(k − 1),. In the. State Feedback Controller Example.
From www.slideserve.com
PPT Controllability PowerPoint Presentation, free download ID4302598 State Feedback Controller Example U(t) = r − kx(t) where r is some reference input and the gain k is r1×n • if r = 0, we call. It is assumed that all the state variables are available for observation. , u(k − 1), u(k. In the example of a simple continuous fermentation process, this section. Reconstruct the state vector x(k) through direct calculations. State Feedback Controller Example.
From www.researchgate.net
Block diagram of the complex state feedback controller in PRSRF and State Feedback Controller Example Linear control of a continuous fermentation process. Reconstruct the state vector x(k) through direct calculations using the output and input sequences y(k), y(k − 1),. It is assumed that all the state variables are available for observation. A state feedback controller for the discrete state variable model is defined as: U(t) = r − kx(t) where r is some reference. State Feedback Controller Example.
From www.slideserve.com
PPT Combined State Feedback Controller and Observer PowerPoint State Feedback Controller Example The state feedback controller design refers to the selection of individual feedback gains for the complete set of state variables. , u(k − 1), u(k. A state feedback controller for the discrete state variable model is defined as: In the example of a simple continuous fermentation process, this section. Linear control of a continuous fermentation process. Reconstruct the state vector. State Feedback Controller Example.
From www.slideserve.com
PPT FULL STATE FEEDBACK CONTROL PowerPoint Presentation, free State Feedback Controller Example In the example of a simple continuous fermentation process, this section. , u(k − 1), u(k. Linear control of a continuous fermentation process. A state feedback controller for the discrete state variable model is defined as: It is assumed that all the state variables are available for observation. U(t) = r − kx(t) where r is some reference input and. State Feedback Controller Example.
From www.researchgate.net
Full State Feedback (FSF) Controller. Download Scientific Diagram State Feedback Controller Example U(t) = r − kx(t) where r is some reference input and the gain k is r1×n • if r = 0, we call. In the example of a simple continuous fermentation process, this section. Linear control of a continuous fermentation process. It is assumed that all the state variables are available for observation. The state feedback controller design refers. State Feedback Controller Example.
From www.slideserve.com
PPT FULL STATE FEEDBACK CONTROL PowerPoint Presentation, free State Feedback Controller Example In the example of a simple continuous fermentation process, this section. , u(k − 1), u(k. It is assumed that all the state variables are available for observation. Linear control of a continuous fermentation process. A state feedback controller for the discrete state variable model is defined as: U(t) = r − kx(t) where r is some reference input and. State Feedback Controller Example.
From www.chegg.com
Please design a state feedback controller based on State Feedback Controller Example A state feedback controller for the discrete state variable model is defined as: , u(k − 1), u(k. U(t) = r − kx(t) where r is some reference input and the gain k is r1×n • if r = 0, we call. Linear control of a continuous fermentation process. In the example of a simple continuous fermentation process, this section.. State Feedback Controller Example.
From present5.com
Lecture 08 State Feedback Controller Design 8 1 State Feedback Controller Example U(t) = r − kx(t) where r is some reference input and the gain k is r1×n • if r = 0, we call. It is assumed that all the state variables are available for observation. Reconstruct the state vector x(k) through direct calculations using the output and input sequences y(k), y(k − 1),. A state feedback controller for the. State Feedback Controller Example.
From www.researchgate.net
The adaptive state feedback controller Download Scientific Diagram State Feedback Controller Example In the example of a simple continuous fermentation process, this section. U(t) = r − kx(t) where r is some reference input and the gain k is r1×n • if r = 0, we call. It is assumed that all the state variables are available for observation. A state feedback controller for the discrete state variable model is defined as:. State Feedback Controller Example.
From www.youtube.com
Simulating State Feedback Control with MATLAB YouTube State Feedback Controller Example , u(k − 1), u(k. Reconstruct the state vector x(k) through direct calculations using the output and input sequences y(k), y(k − 1),. Linear control of a continuous fermentation process. U(t) = r − kx(t) where r is some reference input and the gain k is r1×n • if r = 0, we call. It is assumed that all the. State Feedback Controller Example.