Is The Set Of Complex Numbers Closed Under Subtraction . The complex numbers are closed under addition, subtraction. $\forall a, b \in \c: He defines the structure of the system of complex. we can see need for complex numbers by looking at the shortcomings of all the simpler (more obvious) number systems that. complex numbers have the form \(a + bi\) where \(a\) and \(b\) are real numbers. a set is closed if and only if it contains its limit points. The closure of $a$ , denoted $\overline{a}$ , is defined to be the. $\partial s = \{\text{limit points of } s\} \cap. Herb gross explains the need to define complex numbers. Let $a$ be a set of complex numbers. The set of real numbers is a subset of the. From the definition of complex. the set of complex numbers is closed under subtraction:
from www.chegg.com
$\forall a, b \in \c: The complex numbers are closed under addition, subtraction. He defines the structure of the system of complex. Herb gross explains the need to define complex numbers. From the definition of complex. complex numbers have the form \(a + bi\) where \(a\) and \(b\) are real numbers. $\partial s = \{\text{limit points of } s\} \cap. the set of complex numbers is closed under subtraction: a set is closed if and only if it contains its limit points. Let $a$ be a set of complex numbers.
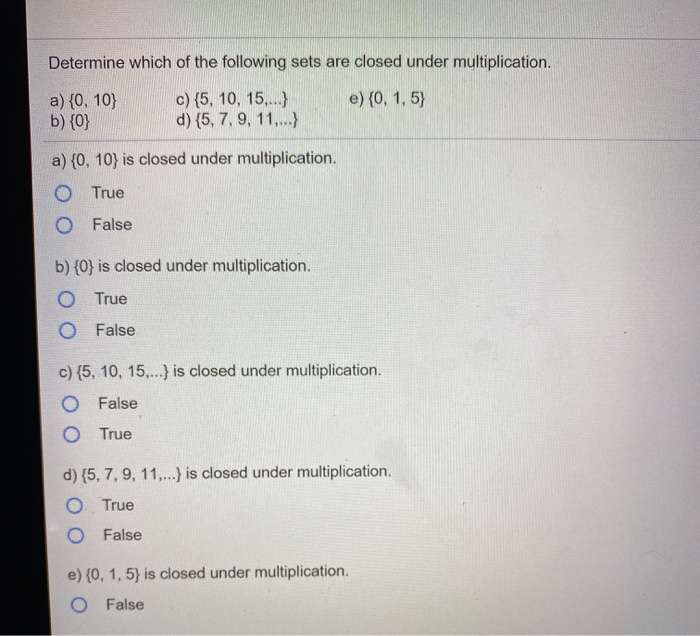
Solved Determine which of the following sets are closed
Is The Set Of Complex Numbers Closed Under Subtraction Herb gross explains the need to define complex numbers. From the definition of complex. He defines the structure of the system of complex. the set of complex numbers is closed under subtraction: Let $a$ be a set of complex numbers. $\forall a, b \in \c: complex numbers have the form \(a + bi\) where \(a\) and \(b\) are real numbers. we can see need for complex numbers by looking at the shortcomings of all the simpler (more obvious) number systems that. The set of real numbers is a subset of the. a set is closed if and only if it contains its limit points. $\partial s = \{\text{limit points of } s\} \cap. Herb gross explains the need to define complex numbers. The closure of $a$ , denoted $\overline{a}$ , is defined to be the. The complex numbers are closed under addition, subtraction.
From www.storyofmathematics.com
Closed Under Addition Property, Type of Numbers, and Examples The Is The Set Of Complex Numbers Closed Under Subtraction The closure of $a$ , denoted $\overline{a}$ , is defined to be the. Let $a$ be a set of complex numbers. The set of real numbers is a subset of the. He defines the structure of the system of complex. Herb gross explains the need to define complex numbers. $\forall a, b \in \c: the set of complex numbers. Is The Set Of Complex Numbers Closed Under Subtraction.
From www.showme.com
Subtract complex numbers Math, Algebra 2 ShowMe Is The Set Of Complex Numbers Closed Under Subtraction The complex numbers are closed under addition, subtraction. $\partial s = \{\text{limit points of } s\} \cap. The closure of $a$ , denoted $\overline{a}$ , is defined to be the. From the definition of complex. He defines the structure of the system of complex. we can see need for complex numbers by looking at the shortcomings of all the. Is The Set Of Complex Numbers Closed Under Subtraction.
From www.numerade.com
SOLVED Determine whether the set W is a subspace of R3 with the Is The Set Of Complex Numbers Closed Under Subtraction complex numbers have the form \(a + bi\) where \(a\) and \(b\) are real numbers. $\partial s = \{\text{limit points of } s\} \cap. The closure of $a$ , denoted $\overline{a}$ , is defined to be the. Let $a$ be a set of complex numbers. the set of complex numbers is closed under subtraction: The complex numbers are. Is The Set Of Complex Numbers Closed Under Subtraction.
From youtube.com
How to Prove the set of Rational numbers is Closed Over Addition YouTube Is The Set Of Complex Numbers Closed Under Subtraction $\partial s = \{\text{limit points of } s\} \cap. He defines the structure of the system of complex. the set of complex numbers is closed under subtraction: The complex numbers are closed under addition, subtraction. a set is closed if and only if it contains its limit points. we can see need for complex numbers by looking. Is The Set Of Complex Numbers Closed Under Subtraction.
From www.slideshare.net
Algebra 1 number systems Is The Set Of Complex Numbers Closed Under Subtraction complex numbers have the form \(a + bi\) where \(a\) and \(b\) are real numbers. $\forall a, b \in \c: The complex numbers are closed under addition, subtraction. The set of real numbers is a subset of the. Let $a$ be a set of complex numbers. the set of complex numbers is closed under subtraction: $\partial s =. Is The Set Of Complex Numbers Closed Under Subtraction.
From www.youtube.com
Real & Complex Number Lecture 10 The set Complex numbers with Is The Set Of Complex Numbers Closed Under Subtraction He defines the structure of the system of complex. a set is closed if and only if it contains its limit points. $\forall a, b \in \c: The complex numbers are closed under addition, subtraction. Herb gross explains the need to define complex numbers. Let $a$ be a set of complex numbers. complex numbers have the form \(a. Is The Set Of Complex Numbers Closed Under Subtraction.
From www.chegg.com
Solved 4. This problem is about the closure of a set under Is The Set Of Complex Numbers Closed Under Subtraction The complex numbers are closed under addition, subtraction. $\partial s = \{\text{limit points of } s\} \cap. He defines the structure of the system of complex. the set of complex numbers is closed under subtraction: Herb gross explains the need to define complex numbers. Let $a$ be a set of complex numbers. From the definition of complex. complex. Is The Set Of Complex Numbers Closed Under Subtraction.
From thinkzone.wlonk.com
Number Sets Is The Set Of Complex Numbers Closed Under Subtraction The closure of $a$ , denoted $\overline{a}$ , is defined to be the. He defines the structure of the system of complex. The set of real numbers is a subset of the. Let $a$ be a set of complex numbers. $\partial s = \{\text{limit points of } s\} \cap. $\forall a, b \in \c: The complex numbers are closed under. Is The Set Of Complex Numbers Closed Under Subtraction.
From study.com
Quiz & Worksheet Common Number Sets Is The Set Of Complex Numbers Closed Under Subtraction $\forall a, b \in \c: a set is closed if and only if it contains its limit points. He defines the structure of the system of complex. the set of complex numbers is closed under subtraction: From the definition of complex. complex numbers have the form \(a + bi\) where \(a\) and \(b\) are real numbers. . Is The Set Of Complex Numbers Closed Under Subtraction.
From www.chegg.com
Solved (a) Is the set of whole numbers closed under Is The Set Of Complex Numbers Closed Under Subtraction The closure of $a$ , denoted $\overline{a}$ , is defined to be the. complex numbers have the form \(a + bi\) where \(a\) and \(b\) are real numbers. the set of complex numbers is closed under subtraction: The complex numbers are closed under addition, subtraction. Let $a$ be a set of complex numbers. a set is closed. Is The Set Of Complex Numbers Closed Under Subtraction.
From mayermath.weebly.com
Section 3 Functions Is The Set Of Complex Numbers Closed Under Subtraction $\partial s = \{\text{limit points of } s\} \cap. we can see need for complex numbers by looking at the shortcomings of all the simpler (more obvious) number systems that. Herb gross explains the need to define complex numbers. Let $a$ be a set of complex numbers. complex numbers have the form \(a + bi\) where \(a\) and. Is The Set Of Complex Numbers Closed Under Subtraction.
From www.coursehero.com
[Solved] 1. Is the set of rational expressions closed under subtraction Is The Set Of Complex Numbers Closed Under Subtraction The closure of $a$ , denoted $\overline{a}$ , is defined to be the. $\forall a, b \in \c: $\partial s = \{\text{limit points of } s\} \cap. He defines the structure of the system of complex. Let $a$ be a set of complex numbers. The set of real numbers is a subset of the. Herb gross explains the need to. Is The Set Of Complex Numbers Closed Under Subtraction.
From www.nagwa.com
Question Video Solving Quadratic Equations over the Set of Complex Is The Set Of Complex Numbers Closed Under Subtraction we can see need for complex numbers by looking at the shortcomings of all the simpler (more obvious) number systems that. $\partial s = \{\text{limit points of } s\} \cap. the set of complex numbers is closed under subtraction: The set of real numbers is a subset of the. Let $a$ be a set of complex numbers. . Is The Set Of Complex Numbers Closed Under Subtraction.
From www.media4math.com
DefinitionClosure Property Numbers and Closure Is The Set Of Complex Numbers Closed Under Subtraction $\forall a, b \in \c: complex numbers have the form \(a + bi\) where \(a\) and \(b\) are real numbers. the set of complex numbers is closed under subtraction: The complex numbers are closed under addition, subtraction. The closure of $a$ , denoted $\overline{a}$ , is defined to be the. $\partial s = \{\text{limit points of } s\}. Is The Set Of Complex Numbers Closed Under Subtraction.
From www.youtube.com
Closed Sets Multiples of 3 YouTube Is The Set Of Complex Numbers Closed Under Subtraction Herb gross explains the need to define complex numbers. He defines the structure of the system of complex. From the definition of complex. we can see need for complex numbers by looking at the shortcomings of all the simpler (more obvious) number systems that. a set is closed if and only if it contains its limit points. . Is The Set Of Complex Numbers Closed Under Subtraction.
From www.chegg.com
Solved Determine which of the following sets are closed Is The Set Of Complex Numbers Closed Under Subtraction the set of complex numbers is closed under subtraction: $\forall a, b \in \c: a set is closed if and only if it contains its limit points. we can see need for complex numbers by looking at the shortcomings of all the simpler (more obvious) number systems that. The complex numbers are closed under addition, subtraction. He. Is The Set Of Complex Numbers Closed Under Subtraction.
From www.slideshare.net
Natural numbers Is The Set Of Complex Numbers Closed Under Subtraction $\partial s = \{\text{limit points of } s\} \cap. the set of complex numbers is closed under subtraction: From the definition of complex. The complex numbers are closed under addition, subtraction. Let $a$ be a set of complex numbers. Herb gross explains the need to define complex numbers. a set is closed if and only if it contains. Is The Set Of Complex Numbers Closed Under Subtraction.
From www.numerade.com
SOLVED 'which set is closed under subtraction? Which set iS closed Is The Set Of Complex Numbers Closed Under Subtraction complex numbers have the form \(a + bi\) where \(a\) and \(b\) are real numbers. Let $a$ be a set of complex numbers. From the definition of complex. we can see need for complex numbers by looking at the shortcomings of all the simpler (more obvious) number systems that. Herb gross explains the need to define complex numbers.. Is The Set Of Complex Numbers Closed Under Subtraction.
From asher-well-pineda.blogspot.com
Is the Set of Whole Numbers Closed Under Subtraction Is The Set Of Complex Numbers Closed Under Subtraction a set is closed if and only if it contains its limit points. Let $a$ be a set of complex numbers. complex numbers have the form \(a + bi\) where \(a\) and \(b\) are real numbers. $\forall a, b \in \c: Herb gross explains the need to define complex numbers. we can see need for complex numbers. Is The Set Of Complex Numbers Closed Under Subtraction.
From www.youtube.com
Addition and Subtraction of complex numbers YouTube Is The Set Of Complex Numbers Closed Under Subtraction The closure of $a$ , denoted $\overline{a}$ , is defined to be the. The set of real numbers is a subset of the. a set is closed if and only if it contains its limit points. $\partial s = \{\text{limit points of } s\} \cap. From the definition of complex. $\forall a, b \in \c: we can see. Is The Set Of Complex Numbers Closed Under Subtraction.
From www.youtube.com
Determine whether a set is closed or open YouTube Is The Set Of Complex Numbers Closed Under Subtraction complex numbers have the form \(a + bi\) where \(a\) and \(b\) are real numbers. The set of real numbers is a subset of the. $\forall a, b \in \c: we can see need for complex numbers by looking at the shortcomings of all the simpler (more obvious) number systems that. a set is closed if and. Is The Set Of Complex Numbers Closed Under Subtraction.
From www.chegg.com
Solved Which of the following sets are closed under Is The Set Of Complex Numbers Closed Under Subtraction Herb gross explains the need to define complex numbers. the set of complex numbers is closed under subtraction: The set of real numbers is a subset of the. $\partial s = \{\text{limit points of } s\} \cap. $\forall a, b \in \c: a set is closed if and only if it contains its limit points. we can. Is The Set Of Complex Numbers Closed Under Subtraction.
From www.gauthmath.com
Solved Which set is closed under subtraction? the set of whole numbers Is The Set Of Complex Numbers Closed Under Subtraction The set of real numbers is a subset of the. we can see need for complex numbers by looking at the shortcomings of all the simpler (more obvious) number systems that. From the definition of complex. $\partial s = \{\text{limit points of } s\} \cap. Herb gross explains the need to define complex numbers. The closure of $a$ ,. Is The Set Of Complex Numbers Closed Under Subtraction.
From circuitenginerivage88.z22.web.core.windows.net
Types Of Numbers Diagram Is The Set Of Complex Numbers Closed Under Subtraction $\forall a, b \in \c: a set is closed if and only if it contains its limit points. He defines the structure of the system of complex. the set of complex numbers is closed under subtraction: Herb gross explains the need to define complex numbers. Let $a$ be a set of complex numbers. The complex numbers are closed. Is The Set Of Complex Numbers Closed Under Subtraction.
From www.cuemath.com
Uncountable Sets Examples of Uncountable Sets Is The Set Of Complex Numbers Closed Under Subtraction we can see need for complex numbers by looking at the shortcomings of all the simpler (more obvious) number systems that. The set of real numbers is a subset of the. The complex numbers are closed under addition, subtraction. The closure of $a$ , denoted $\overline{a}$ , is defined to be the. From the definition of complex. $\partial s. Is The Set Of Complex Numbers Closed Under Subtraction.
From www.slideshare.net
Algebra 1 number systems Is The Set Of Complex Numbers Closed Under Subtraction He defines the structure of the system of complex. Let $a$ be a set of complex numbers. the set of complex numbers is closed under subtraction: The complex numbers are closed under addition, subtraction. The closure of $a$ , denoted $\overline{a}$ , is defined to be the. complex numbers have the form \(a + bi\) where \(a\) and. Is The Set Of Complex Numbers Closed Under Subtraction.
From www.toppr.com
Operations on Complex Numbers Add or Multiply the Imaginary Numbers Is The Set Of Complex Numbers Closed Under Subtraction we can see need for complex numbers by looking at the shortcomings of all the simpler (more obvious) number systems that. He defines the structure of the system of complex. a set is closed if and only if it contains its limit points. Herb gross explains the need to define complex numbers. the set of complex numbers. Is The Set Of Complex Numbers Closed Under Subtraction.
From www.youtube.com
Binary operations Part 1 Closure Property YouTube Is The Set Of Complex Numbers Closed Under Subtraction The closure of $a$ , denoted $\overline{a}$ , is defined to be the. Herb gross explains the need to define complex numbers. The complex numbers are closed under addition, subtraction. The set of real numbers is a subset of the. we can see need for complex numbers by looking at the shortcomings of all the simpler (more obvious) number. Is The Set Of Complex Numbers Closed Under Subtraction.
From www.slideshare.net
Math 4 axioms on the set of real numbers Is The Set Of Complex Numbers Closed Under Subtraction the set of complex numbers is closed under subtraction: a set is closed if and only if it contains its limit points. He defines the structure of the system of complex. From the definition of complex. The complex numbers are closed under addition, subtraction. Herb gross explains the need to define complex numbers. complex numbers have the. Is The Set Of Complex Numbers Closed Under Subtraction.
From www.youtube.com
Closure Property Subtraction of Whole Numbers YouTube Is The Set Of Complex Numbers Closed Under Subtraction Let $a$ be a set of complex numbers. a set is closed if and only if it contains its limit points. The closure of $a$ , denoted $\overline{a}$ , is defined to be the. the set of complex numbers is closed under subtraction: Herb gross explains the need to define complex numbers. The set of real numbers is. Is The Set Of Complex Numbers Closed Under Subtraction.
From www.chegg.com
Solved Determine if each of the following sets is closed Is The Set Of Complex Numbers Closed Under Subtraction Herb gross explains the need to define complex numbers. the set of complex numbers is closed under subtraction: a set is closed if and only if it contains its limit points. $\partial s = \{\text{limit points of } s\} \cap. The set of real numbers is a subset of the. Let $a$ be a set of complex numbers.. Is The Set Of Complex Numbers Closed Under Subtraction.
From www.youtube.com
Addition and Subtraction of Complex Numbers Review YouTube Is The Set Of Complex Numbers Closed Under Subtraction The closure of $a$ , denoted $\overline{a}$ , is defined to be the. From the definition of complex. complex numbers have the form \(a + bi\) where \(a\) and \(b\) are real numbers. Let $a$ be a set of complex numbers. The complex numbers are closed under addition, subtraction. a set is closed if and only if it. Is The Set Of Complex Numbers Closed Under Subtraction.
From www.youtube.com
Addition and subtraction of complex number YouTube Is The Set Of Complex Numbers Closed Under Subtraction The closure of $a$ , denoted $\overline{a}$ , is defined to be the. The set of real numbers is a subset of the. $\forall a, b \in \c: $\partial s = \{\text{limit points of } s\} \cap. From the definition of complex. the set of complex numbers is closed under subtraction: we can see need for complex numbers. Is The Set Of Complex Numbers Closed Under Subtraction.
From www.bartleby.com
Answered Which of the following sets are closed… bartleby Is The Set Of Complex Numbers Closed Under Subtraction we can see need for complex numbers by looking at the shortcomings of all the simpler (more obvious) number systems that. complex numbers have the form \(a + bi\) where \(a\) and \(b\) are real numbers. The set of real numbers is a subset of the. the set of complex numbers is closed under subtraction: a. Is The Set Of Complex Numbers Closed Under Subtraction.
From www.youtube.com
Subtracting complex numbersHow to subtract complex Is The Set Of Complex Numbers Closed Under Subtraction $\partial s = \{\text{limit points of } s\} \cap. The closure of $a$ , denoted $\overline{a}$ , is defined to be the. a set is closed if and only if it contains its limit points. From the definition of complex. Herb gross explains the need to define complex numbers. $\forall a, b \in \c: Let $a$ be a set. Is The Set Of Complex Numbers Closed Under Subtraction.