Bicg Matlab Algorithm . This paper seeks to explain why bicg converges so well, and what conditions can cause bicg to behave poorly. The biconjugate gradients stabilized (bicgstab) algorithm was developed to improve on the bicg algorithm by using restarted gmres steps to mitigate the irregular convergence behavior. The biconjugate gradient stabilized method combines ideas of both cgs and sor. The biconjugate gradient stabilized (bcgstab) method was developed to solve nonsymmetric linear systems while avoiding. X = bicg(a,b) attempts to solve the system of linear equations a*x = b for x. The biconjugate gradients (bicg) algorithm was developed to generalize the conjugate gradient (cg) method to nonsymmetric systems. We use tools such as the. The coefficient matrix a must be square and the right hand side.
from engineerstutor.com
X = bicg(a,b) attempts to solve the system of linear equations a*x = b for x. We use tools such as the. The biconjugate gradient stabilized method combines ideas of both cgs and sor. This paper seeks to explain why bicg converges so well, and what conditions can cause bicg to behave poorly. The coefficient matrix a must be square and the right hand side. The biconjugate gradient stabilized (bcgstab) method was developed to solve nonsymmetric linear systems while avoiding. The biconjugate gradients (bicg) algorithm was developed to generalize the conjugate gradient (cg) method to nonsymmetric systems. The biconjugate gradients stabilized (bicgstab) algorithm was developed to improve on the bicg algorithm by using restarted gmres steps to mitigate the irregular convergence behavior.
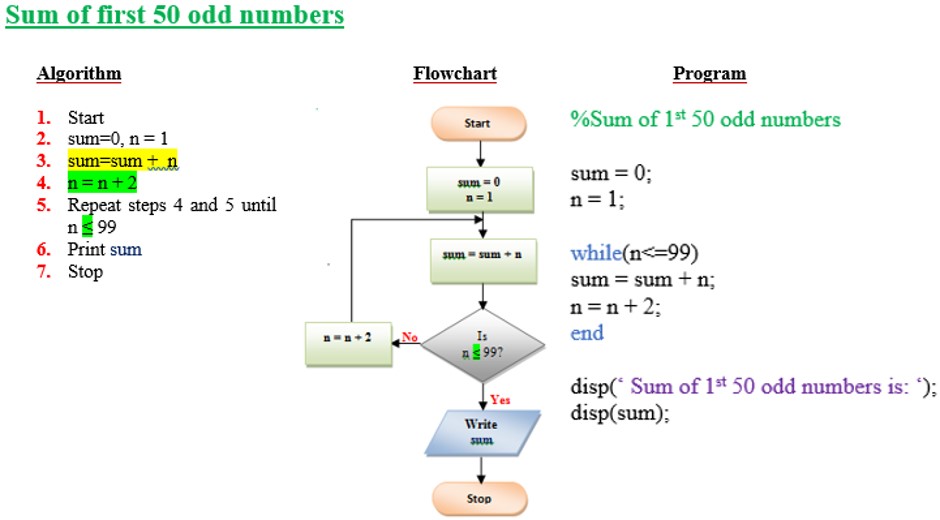
Examples of Algorithms and Flow charts with MATLAB programs
Bicg Matlab Algorithm The biconjugate gradient stabilized method combines ideas of both cgs and sor. The biconjugate gradient stabilized method combines ideas of both cgs and sor. We use tools such as the. The biconjugate gradient stabilized (bcgstab) method was developed to solve nonsymmetric linear systems while avoiding. The biconjugate gradients (bicg) algorithm was developed to generalize the conjugate gradient (cg) method to nonsymmetric systems. The biconjugate gradients stabilized (bicgstab) algorithm was developed to improve on the bicg algorithm by using restarted gmres steps to mitigate the irregular convergence behavior. This paper seeks to explain why bicg converges so well, and what conditions can cause bicg to behave poorly. X = bicg(a,b) attempts to solve the system of linear equations a*x = b for x. The coefficient matrix a must be square and the right hand side.
From engineerstutor.com
Examples of Algorithms and Flow charts with MATLAB programs Bicg Matlab Algorithm The biconjugate gradients stabilized (bicgstab) algorithm was developed to improve on the bicg algorithm by using restarted gmres steps to mitigate the irregular convergence behavior. X = bicg(a,b) attempts to solve the system of linear equations a*x = b for x. The biconjugate gradient stabilized method combines ideas of both cgs and sor. This paper seeks to explain why bicg. Bicg Matlab Algorithm.
From www.chegg.com
Objectives Develop and utilize a Matlab algorithm Bicg Matlab Algorithm The biconjugate gradient stabilized (bcgstab) method was developed to solve nonsymmetric linear systems while avoiding. X = bicg(a,b) attempts to solve the system of linear equations a*x = b for x. The biconjugate gradient stabilized method combines ideas of both cgs and sor. The biconjugate gradients stabilized (bicgstab) algorithm was developed to improve on the bicg algorithm by using restarted. Bicg Matlab Algorithm.
From www.researchgate.net
The algorithm and flowchart of MATLAB programming Download Scientific Bicg Matlab Algorithm The coefficient matrix a must be square and the right hand side. The biconjugate gradient stabilized method combines ideas of both cgs and sor. The biconjugate gradients (bicg) algorithm was developed to generalize the conjugate gradient (cg) method to nonsymmetric systems. X = bicg(a,b) attempts to solve the system of linear equations a*x = b for x. The biconjugate gradient. Bicg Matlab Algorithm.
From www.researchgate.net
Simple MATLAB MCMC method algorithm for reliability estimation Bicg Matlab Algorithm The biconjugate gradient stabilized (bcgstab) method was developed to solve nonsymmetric linear systems while avoiding. The biconjugate gradient stabilized method combines ideas of both cgs and sor. The biconjugate gradients stabilized (bicgstab) algorithm was developed to improve on the bicg algorithm by using restarted gmres steps to mitigate the irregular convergence behavior. The biconjugate gradients (bicg) algorithm was developed to. Bicg Matlab Algorithm.
From www.researchgate.net
Algorithm for analytic calculations using MATLAB code. Download Bicg Matlab Algorithm This paper seeks to explain why bicg converges so well, and what conditions can cause bicg to behave poorly. The biconjugate gradient stabilized (bcgstab) method was developed to solve nonsymmetric linear systems while avoiding. The biconjugate gradient stabilized method combines ideas of both cgs and sor. The biconjugate gradients (bicg) algorithm was developed to generalize the conjugate gradient (cg) method. Bicg Matlab Algorithm.
From de.mathworks.com
Accelerating MATLAB Algorithms and Applications MATLAB & Simulink Bicg Matlab Algorithm The biconjugate gradients (bicg) algorithm was developed to generalize the conjugate gradient (cg) method to nonsymmetric systems. The biconjugate gradient stabilized (bcgstab) method was developed to solve nonsymmetric linear systems while avoiding. The biconjugate gradients stabilized (bicgstab) algorithm was developed to improve on the bicg algorithm by using restarted gmres steps to mitigate the irregular convergence behavior. We use tools. Bicg Matlab Algorithm.
From www.semanticscholar.org
Figure 1 from The CCM Based Implementation of the Parallel Variant of Bicg Matlab Algorithm The biconjugate gradient stabilized method combines ideas of both cgs and sor. This paper seeks to explain why bicg converges so well, and what conditions can cause bicg to behave poorly. X = bicg(a,b) attempts to solve the system of linear equations a*x = b for x. The biconjugate gradients stabilized (bicgstab) algorithm was developed to improve on the bicg. Bicg Matlab Algorithm.
From engineerstutor.com
Examples of Algorithms and Flow charts with MATLAB programs Bicg Matlab Algorithm The biconjugate gradients (bicg) algorithm was developed to generalize the conjugate gradient (cg) method to nonsymmetric systems. This paper seeks to explain why bicg converges so well, and what conditions can cause bicg to behave poorly. X = bicg(a,b) attempts to solve the system of linear equations a*x = b for x. The coefficient matrix a must be square and. Bicg Matlab Algorithm.
From engineersplanet.com
Basic Elements of MATLAB Programming Engineer's Bicg Matlab Algorithm The biconjugate gradient stabilized method combines ideas of both cgs and sor. The coefficient matrix a must be square and the right hand side. X = bicg(a,b) attempts to solve the system of linear equations a*x = b for x. The biconjugate gradient stabilized (bcgstab) method was developed to solve nonsymmetric linear systems while avoiding. The biconjugate gradients (bicg) algorithm. Bicg Matlab Algorithm.
From learnwithpanda.com
Algorithm General Concept, Matlab Code, and Example Bicg Matlab Algorithm X = bicg(a,b) attempts to solve the system of linear equations a*x = b for x. The coefficient matrix a must be square and the right hand side. We use tools such as the. The biconjugate gradients stabilized (bicgstab) algorithm was developed to improve on the bicg algorithm by using restarted gmres steps to mitigate the irregular convergence behavior. The. Bicg Matlab Algorithm.
From dokumen.tips
(DOCX) How Do I Implement My MATLAB Algorithm in an FPGA DOKUMEN.TIPS Bicg Matlab Algorithm The biconjugate gradient stabilized (bcgstab) method was developed to solve nonsymmetric linear systems while avoiding. The biconjugate gradient stabilized method combines ideas of both cgs and sor. X = bicg(a,b) attempts to solve the system of linear equations a*x = b for x. The coefficient matrix a must be square and the right hand side. We use tools such as. Bicg Matlab Algorithm.
From www.researchgate.net
Convergence of BiCGSTAB algorithm with Jacobi preconditioning for the Bicg Matlab Algorithm The biconjugate gradient stabilized method combines ideas of both cgs and sor. The coefficient matrix a must be square and the right hand side. The biconjugate gradients (bicg) algorithm was developed to generalize the conjugate gradient (cg) method to nonsymmetric systems. This paper seeks to explain why bicg converges so well, and what conditions can cause bicg to behave poorly.. Bicg Matlab Algorithm.
From www.researchgate.net
Convergence of BiCGSTAB algorithm with Jacobi preconditioning for the Bicg Matlab Algorithm X = bicg(a,b) attempts to solve the system of linear equations a*x = b for x. The biconjugate gradient stabilized method combines ideas of both cgs and sor. The coefficient matrix a must be square and the right hand side. This paper seeks to explain why bicg converges so well, and what conditions can cause bicg to behave poorly. The. Bicg Matlab Algorithm.
From www.youtube.com
Thomas Algorithm MATLAB Code/ Program YouTube Bicg Matlab Algorithm X = bicg(a,b) attempts to solve the system of linear equations a*x = b for x. This paper seeks to explain why bicg converges so well, and what conditions can cause bicg to behave poorly. The coefficient matrix a must be square and the right hand side. The biconjugate gradients stabilized (bicgstab) algorithm was developed to improve on the bicg. Bicg Matlab Algorithm.
From www.researchgate.net
Convergence history of BlGPBiCG, BlBiCGSTAB, and BlBiCG algorithms Bicg Matlab Algorithm We use tools such as the. X = bicg(a,b) attempts to solve the system of linear equations a*x = b for x. This paper seeks to explain why bicg converges so well, and what conditions can cause bicg to behave poorly. The biconjugate gradients (bicg) algorithm was developed to generalize the conjugate gradient (cg) method to nonsymmetric systems. The biconjugate. Bicg Matlab Algorithm.
From ppt-online.org
A block version of Gmres, Bicg, Bicgstab for linear systems with Bicg Matlab Algorithm X = bicg(a,b) attempts to solve the system of linear equations a*x = b for x. We use tools such as the. The biconjugate gradients (bicg) algorithm was developed to generalize the conjugate gradient (cg) method to nonsymmetric systems. The biconjugate gradient stabilized (bcgstab) method was developed to solve nonsymmetric linear systems while avoiding. The biconjugate gradients stabilized (bicgstab) algorithm. Bicg Matlab Algorithm.
From www.youtube.com
Automorphic number in MATLAB (Algorithm & code) YouTube Bicg Matlab Algorithm X = bicg(a,b) attempts to solve the system of linear equations a*x = b for x. The biconjugate gradient stabilized method combines ideas of both cgs and sor. The biconjugate gradient stabilized (bcgstab) method was developed to solve nonsymmetric linear systems while avoiding. This paper seeks to explain why bicg converges so well, and what conditions can cause bicg to. Bicg Matlab Algorithm.
From engineerstutor.com
Examples of Algorithms and Flow charts with MATLAB programs Bicg Matlab Algorithm The biconjugate gradient stabilized (bcgstab) method was developed to solve nonsymmetric linear systems while avoiding. This paper seeks to explain why bicg converges so well, and what conditions can cause bicg to behave poorly. The biconjugate gradients stabilized (bicgstab) algorithm was developed to improve on the bicg algorithm by using restarted gmres steps to mitigate the irregular convergence behavior. The. Bicg Matlab Algorithm.
From learnwithpanda.com
How to Use MultiObjective Algorithm Solver in Matlab Bicg Matlab Algorithm The biconjugate gradient stabilized method combines ideas of both cgs and sor. The biconjugate gradient stabilized (bcgstab) method was developed to solve nonsymmetric linear systems while avoiding. This paper seeks to explain why bicg converges so well, and what conditions can cause bicg to behave poorly. X = bicg(a,b) attempts to solve the system of linear equations a*x = b. Bicg Matlab Algorithm.
From www.chegg.com
Solved IMPORTANT!!! For b), please write a MATLAB algorithm Bicg Matlab Algorithm X = bicg(a,b) attempts to solve the system of linear equations a*x = b for x. The biconjugate gradients stabilized (bicgstab) algorithm was developed to improve on the bicg algorithm by using restarted gmres steps to mitigate the irregular convergence behavior. The biconjugate gradient stabilized (bcgstab) method was developed to solve nonsymmetric linear systems while avoiding. The coefficient matrix a. Bicg Matlab Algorithm.
From www.researchgate.net
MATLAB algorithm flow chart for wear loosening numerical analysis of Bicg Matlab Algorithm The biconjugate gradients (bicg) algorithm was developed to generalize the conjugate gradient (cg) method to nonsymmetric systems. The biconjugate gradients stabilized (bicgstab) algorithm was developed to improve on the bicg algorithm by using restarted gmres steps to mitigate the irregular convergence behavior. We use tools such as the. This paper seeks to explain why bicg converges so well, and what. Bicg Matlab Algorithm.
From www.youtube.com
How to Build Algorithm Code in Matlab (Live Chat with Me) YouTube Bicg Matlab Algorithm We use tools such as the. The biconjugate gradients (bicg) algorithm was developed to generalize the conjugate gradient (cg) method to nonsymmetric systems. The biconjugate gradients stabilized (bicgstab) algorithm was developed to improve on the bicg algorithm by using restarted gmres steps to mitigate the irregular convergence behavior. The biconjugate gradient stabilized method combines ideas of both cgs and sor.. Bicg Matlab Algorithm.
From www.researchgate.net
Proposed algorithm for MATLAB code Download Scientific Diagram Bicg Matlab Algorithm The coefficient matrix a must be square and the right hand side. This paper seeks to explain why bicg converges so well, and what conditions can cause bicg to behave poorly. The biconjugate gradient stabilized method combines ideas of both cgs and sor. X = bicg(a,b) attempts to solve the system of linear equations a*x = b for x. The. Bicg Matlab Algorithm.
From www.researchgate.net
The flow chart of the MATLAB® algorithm used in the numerical approach Bicg Matlab Algorithm X = bicg(a,b) attempts to solve the system of linear equations a*x = b for x. We use tools such as the. The biconjugate gradients stabilized (bicgstab) algorithm was developed to improve on the bicg algorithm by using restarted gmres steps to mitigate the irregular convergence behavior. The biconjugate gradient stabilized (bcgstab) method was developed to solve nonsymmetric linear systems. Bicg Matlab Algorithm.
From www.mathworks.com
MATLAB Coder MATLAB Bicg Matlab Algorithm X = bicg(a,b) attempts to solve the system of linear equations a*x = b for x. The biconjugate gradients stabilized (bicgstab) algorithm was developed to improve on the bicg algorithm by using restarted gmres steps to mitigate the irregular convergence behavior. We use tools such as the. The biconjugate gradient stabilized method combines ideas of both cgs and sor. The. Bicg Matlab Algorithm.
From www.youtube.com
Algorithm Solver in Matlab vs MultiStart Algorithm Bicg Matlab Algorithm We use tools such as the. This paper seeks to explain why bicg converges so well, and what conditions can cause bicg to behave poorly. The biconjugate gradient stabilized method combines ideas of both cgs and sor. The biconjugate gradient stabilized (bcgstab) method was developed to solve nonsymmetric linear systems while avoiding. X = bicg(a,b) attempts to solve the system. Bicg Matlab Algorithm.
From www.semanticscholar.org
Figure 6.2 from Preconditioned Chebyshev BiCG for parameterized linear Bicg Matlab Algorithm The biconjugate gradients stabilized (bicgstab) algorithm was developed to improve on the bicg algorithm by using restarted gmres steps to mitigate the irregular convergence behavior. The biconjugate gradient stabilized (bcgstab) method was developed to solve nonsymmetric linear systems while avoiding. The biconjugate gradients (bicg) algorithm was developed to generalize the conjugate gradient (cg) method to nonsymmetric systems. This paper seeks. Bicg Matlab Algorithm.
From www.researchgate.net
Algorithm 3 The procedure for preconditioned BiCG. Download Bicg Matlab Algorithm We use tools such as the. This paper seeks to explain why bicg converges so well, and what conditions can cause bicg to behave poorly. The biconjugate gradient stabilized method combines ideas of both cgs and sor. The biconjugate gradients stabilized (bicgstab) algorithm was developed to improve on the bicg algorithm by using restarted gmres steps to mitigate the irregular. Bicg Matlab Algorithm.
From www.mathworks.com
Accelerating MATLAB Algorithms and Applications MATLAB & Simulink Bicg Matlab Algorithm The biconjugate gradients (bicg) algorithm was developed to generalize the conjugate gradient (cg) method to nonsymmetric systems. We use tools such as the. X = bicg(a,b) attempts to solve the system of linear equations a*x = b for x. The biconjugate gradients stabilized (bicgstab) algorithm was developed to improve on the bicg algorithm by using restarted gmres steps to mitigate. Bicg Matlab Algorithm.
From learnwithpanda.com
Matlab Code of a Robust Algorithm For Global Optimization Bicg Matlab Algorithm X = bicg(a,b) attempts to solve the system of linear equations a*x = b for x. We use tools such as the. The biconjugate gradient stabilized (bcgstab) method was developed to solve nonsymmetric linear systems while avoiding. The biconjugate gradient stabilized method combines ideas of both cgs and sor. The biconjugate gradients (bicg) algorithm was developed to generalize the conjugate. Bicg Matlab Algorithm.
From ppt-online.org
A block version of Gmres, Bicg, Bicgstab for linear systems with Bicg Matlab Algorithm The biconjugate gradients stabilized (bicgstab) algorithm was developed to improve on the bicg algorithm by using restarted gmres steps to mitigate the irregular convergence behavior. The biconjugate gradients (bicg) algorithm was developed to generalize the conjugate gradient (cg) method to nonsymmetric systems. This paper seeks to explain why bicg converges so well, and what conditions can cause bicg to behave. Bicg Matlab Algorithm.
From www.researchgate.net
Flow Chart of the Matlab Algorithm Download Scientific Diagram Bicg Matlab Algorithm The biconjugate gradients (bicg) algorithm was developed to generalize the conjugate gradient (cg) method to nonsymmetric systems. We use tools such as the. The biconjugate gradient stabilized method combines ideas of both cgs and sor. The coefficient matrix a must be square and the right hand side. X = bicg(a,b) attempts to solve the system of linear equations a*x =. Bicg Matlab Algorithm.
From www.mathworks.com
MATLAB to FPGA in 5 Steps Video MATLAB & Simulink Bicg Matlab Algorithm The biconjugate gradient stabilized (bcgstab) method was developed to solve nonsymmetric linear systems while avoiding. We use tools such as the. The biconjugate gradient stabilized method combines ideas of both cgs and sor. The biconjugate gradients stabilized (bicgstab) algorithm was developed to improve on the bicg algorithm by using restarted gmres steps to mitigate the irregular convergence behavior. X =. Bicg Matlab Algorithm.
From www.youtube.com
Binary Algorithm in Matlab (Matlab Code) YouTube Bicg Matlab Algorithm The biconjugate gradients (bicg) algorithm was developed to generalize the conjugate gradient (cg) method to nonsymmetric systems. The biconjugate gradient stabilized (bcgstab) method was developed to solve nonsymmetric linear systems while avoiding. The coefficient matrix a must be square and the right hand side. The biconjugate gradient stabilized method combines ideas of both cgs and sor. This paper seeks to. Bicg Matlab Algorithm.
From www.mdpi.com
Proceedings Free FullText Matlab Framework for Image Processing Bicg Matlab Algorithm The biconjugate gradient stabilized method combines ideas of both cgs and sor. X = bicg(a,b) attempts to solve the system of linear equations a*x = b for x. This paper seeks to explain why bicg converges so well, and what conditions can cause bicg to behave poorly. The biconjugate gradients stabilized (bicgstab) algorithm was developed to improve on the bicg. Bicg Matlab Algorithm.