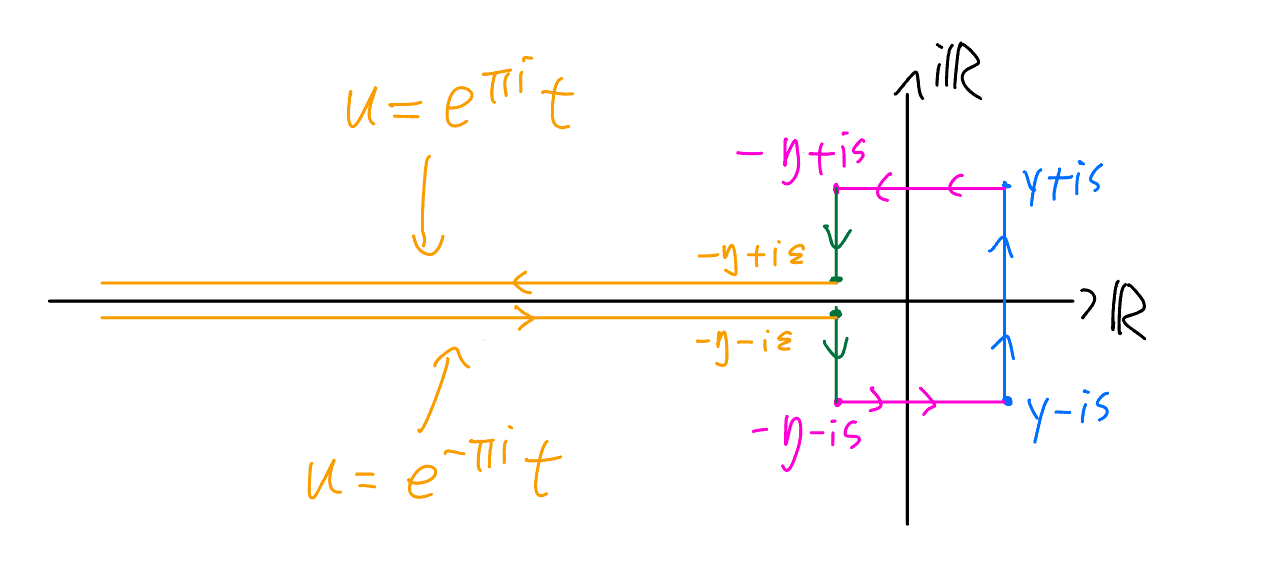Partitions Asymptotic Formulas . Let a = {a1, a2,. Let pa(n) denote the number of partitions of n with parts belonging to a. Let p a;b(n) denote the number of. A partition of an integer n n is a way of writing n n as a sum of integers. The asymptotic formula for partitions provides a way to estimate the number of ways an integer can be expressed as the sum of positive integers, known. The asymptotic formula is an approximation of the leading term within an asymptotic expansion formulated by ramanujan and hardy: N 0gwhere n is an integer. Asymptotics of partition functions daniel m. , ak} be a set of k relatively prime positive integers. Demystifying the asymptotic expression for the partition function. Let s a;b = fan + b :
from travorlzh.github.io
Demystifying the asymptotic expression for the partition function. N 0gwhere n is an integer. Let s a;b = fan + b : Let p a;b(n) denote the number of. Asymptotics of partition functions daniel m. , ak} be a set of k relatively prime positive integers. The asymptotic formula for partitions provides a way to estimate the number of ways an integer can be expressed as the sum of positive integers, known. A partition of an integer n n is a way of writing n n as a sum of integers. The asymptotic formula is an approximation of the leading term within an asymptotic expansion formulated by ramanujan and hardy: Let a = {a1, a2,.
Asymptotic theory of integer partitions Travor's Home Page
Partitions Asymptotic Formulas Let a = {a1, a2,. Let s a;b = fan + b : The asymptotic formula for partitions provides a way to estimate the number of ways an integer can be expressed as the sum of positive integers, known. Let a = {a1, a2,. Demystifying the asymptotic expression for the partition function. N 0gwhere n is an integer. Let p a;b(n) denote the number of. The asymptotic formula is an approximation of the leading term within an asymptotic expansion formulated by ramanujan and hardy: Asymptotics of partition functions daniel m. Let pa(n) denote the number of partitions of n with parts belonging to a. , ak} be a set of k relatively prime positive integers. A partition of an integer n n is a way of writing n n as a sum of integers.
From mathmonks.com
Oblique (Slant) Asymptote Definition, Formulas, Rules, and Graphs Partitions Asymptotic Formulas , ak} be a set of k relatively prime positive integers. Let p a;b(n) denote the number of. Let s a;b = fan + b : N 0gwhere n is an integer. Let pa(n) denote the number of partitions of n with parts belonging to a. A partition of an integer n n is a way of writing n n. Partitions Asymptotic Formulas.
From dotnettutorials.net
Properties of Asymptotic Notations in Data Structure Dot Net Tutorials Partitions Asymptotic Formulas Let p a;b(n) denote the number of. A partition of an integer n n is a way of writing n n as a sum of integers. Let a = {a1, a2,. Let pa(n) denote the number of partitions of n with parts belonging to a. Demystifying the asymptotic expression for the partition function. Let s a;b = fan + b. Partitions Asymptotic Formulas.
From www.slideshare.net
Asymptotic notation Partitions Asymptotic Formulas Let a = {a1, a2,. Asymptotics of partition functions daniel m. The asymptotic formula for partitions provides a way to estimate the number of ways an integer can be expressed as the sum of positive integers, known. Let s a;b = fan + b : Let p a;b(n) denote the number of. Let pa(n) denote the number of partitions of. Partitions Asymptotic Formulas.
From www.academia.edu
(PDF) Ramanujan's asymptotic partition formula Dr. Jack Dikian Partitions Asymptotic Formulas The asymptotic formula is an approximation of the leading term within an asymptotic expansion formulated by ramanujan and hardy: The asymptotic formula for partitions provides a way to estimate the number of ways an integer can be expressed as the sum of positive integers, known. Let a = {a1, a2,. Let p a;b(n) denote the number of. N 0gwhere n. Partitions Asymptotic Formulas.
From studylib.net
Asymptotic notations Partitions Asymptotic Formulas Let a = {a1, a2,. Demystifying the asymptotic expression for the partition function. Let pa(n) denote the number of partitions of n with parts belonging to a. Asymptotics of partition functions daniel m. Let p a;b(n) denote the number of. The asymptotic formula for partitions provides a way to estimate the number of ways an integer can be expressed as. Partitions Asymptotic Formulas.
From www.researchgate.net
(PDF) ON ASYMPTOTIC FORMULA OF THE PARTITION FUNCTION p_A(n) Partitions Asymptotic Formulas Let a = {a1, a2,. N 0gwhere n is an integer. The asymptotic formula for partitions provides a way to estimate the number of ways an integer can be expressed as the sum of positive integers, known. The asymptotic formula is an approximation of the leading term within an asymptotic expansion formulated by ramanujan and hardy: Demystifying the asymptotic expression. Partitions Asymptotic Formulas.
From www.academia.edu
(PDF) On the analysis of asymptotic formulas for the density of string Partitions Asymptotic Formulas The asymptotic formula for partitions provides a way to estimate the number of ways an integer can be expressed as the sum of positive integers, known. Let a = {a1, a2,. Demystifying the asymptotic expression for the partition function. Asymptotics of partition functions daniel m. Let pa(n) denote the number of partitions of n with parts belonging to a. Let. Partitions Asymptotic Formulas.
From www.scribd.com
Asymptotic Behavior of Number of Partitions PDF Partitions Asymptotic Formulas A partition of an integer n n is a way of writing n n as a sum of integers. Let pa(n) denote the number of partitions of n with parts belonging to a. The asymptotic formula is an approximation of the leading term within an asymptotic expansion formulated by ramanujan and hardy: Let s a;b = fan + b :. Partitions Asymptotic Formulas.
From www.slideserve.com
PPT ASYMPTOTES TUTORIAL PowerPoint Presentation, free download ID Partitions Asymptotic Formulas N 0gwhere n is an integer. Let p a;b(n) denote the number of. The asymptotic formula for partitions provides a way to estimate the number of ways an integer can be expressed as the sum of positive integers, known. Let pa(n) denote the number of partitions of n with parts belonging to a. Let s a;b = fan + b. Partitions Asymptotic Formulas.
From www.researchgate.net
(PDF) Asymptotic expansions for partitions generated by infinite products Partitions Asymptotic Formulas Let pa(n) denote the number of partitions of n with parts belonging to a. The asymptotic formula is an approximation of the leading term within an asymptotic expansion formulated by ramanujan and hardy: N 0gwhere n is an integer. The asymptotic formula for partitions provides a way to estimate the number of ways an integer can be expressed as the. Partitions Asymptotic Formulas.
From www.researchgate.net
(PDF) Asymptotic formula for the M_2ranks of overpartitions Partitions Asymptotic Formulas Demystifying the asymptotic expression for the partition function. A partition of an integer n n is a way of writing n n as a sum of integers. Let a = {a1, a2,. Let pa(n) denote the number of partitions of n with parts belonging to a. Let s a;b = fan + b : Let p a;b(n) denote the number. Partitions Asymptotic Formulas.
From iteducationcourse.com
Horizontal Asymptotes Definition, Rules, Equation and more Partitions Asymptotic Formulas A partition of an integer n n is a way of writing n n as a sum of integers. The asymptotic formula for partitions provides a way to estimate the number of ways an integer can be expressed as the sum of positive integers, known. Let p a;b(n) denote the number of. N 0gwhere n is an integer. Demystifying the. Partitions Asymptotic Formulas.
From msalg22020.blogspot.com
Unit 4.6 Finding Horizontal Asymptotes Algebraically Partitions Asymptotic Formulas Let s a;b = fan + b : Let a = {a1, a2,. , ak} be a set of k relatively prime positive integers. Demystifying the asymptotic expression for the partition function. Let pa(n) denote the number of partitions of n with parts belonging to a. Let p a;b(n) denote the number of. The asymptotic formula for partitions provides a. Partitions Asymptotic Formulas.
From www.scribd.com
HardyRamanujan Asymptotic Partition Formula PDF Partitions Asymptotic Formulas The asymptotic formula for partitions provides a way to estimate the number of ways an integer can be expressed as the sum of positive integers, known. N 0gwhere n is an integer. Let p a;b(n) denote the number of. A partition of an integer n n is a way of writing n n as a sum of integers. The asymptotic. Partitions Asymptotic Formulas.
From www.semanticscholar.org
Table 4 from Asymptotic formulas for elliptic integrals Semantic Scholar Partitions Asymptotic Formulas Let p a;b(n) denote the number of. A partition of an integer n n is a way of writing n n as a sum of integers. The asymptotic formula for partitions provides a way to estimate the number of ways an integer can be expressed as the sum of positive integers, known. Let s a;b = fan + b :. Partitions Asymptotic Formulas.
From www.researchgate.net
(PDF) Asymptotics for the twisted etaproduct and applications to sign Partitions Asymptotic Formulas A partition of an integer n n is a way of writing n n as a sum of integers. Let s a;b = fan + b : Let a = {a1, a2,. Demystifying the asymptotic expression for the partition function. Let p a;b(n) denote the number of. , ak} be a set of k relatively prime positive integers. Asymptotics of. Partitions Asymptotic Formulas.
From www.slideserve.com
PPT Emergent SpaceTime and and Induced Gravity PowerPoint Partitions Asymptotic Formulas Asymptotics of partition functions daniel m. Let a = {a1, a2,. The asymptotic formula is an approximation of the leading term within an asymptotic expansion formulated by ramanujan and hardy: A partition of an integer n n is a way of writing n n as a sum of integers. Let s a;b = fan + b : Demystifying the asymptotic. Partitions Asymptotic Formulas.
From www.researchgate.net
(PDF) Errata for ”An asymptotic formula for Cayley’s double partition Partitions Asymptotic Formulas N 0gwhere n is an integer. Asymptotics of partition functions daniel m. The asymptotic formula is an approximation of the leading term within an asymptotic expansion formulated by ramanujan and hardy: Let a = {a1, a2,. Let pa(n) denote the number of partitions of n with parts belonging to a. The asymptotic formula for partitions provides a way to estimate. Partitions Asymptotic Formulas.
From www.semanticscholar.org
Table 1 from Asymptotic formulas for elliptic integrals Semantic Scholar Partitions Asymptotic Formulas A partition of an integer n n is a way of writing n n as a sum of integers. The asymptotic formula is an approximation of the leading term within an asymptotic expansion formulated by ramanujan and hardy: Demystifying the asymptotic expression for the partition function. , ak} be a set of k relatively prime positive integers. Asymptotics of partition. Partitions Asymptotic Formulas.
From giasutamtaiduc.com
Asymptote Formula ⭐️⭐️⭐️⭐️⭐ Partitions Asymptotic Formulas Let a = {a1, a2,. N 0gwhere n is an integer. Asymptotics of partition functions daniel m. The asymptotic formula for partitions provides a way to estimate the number of ways an integer can be expressed as the sum of positive integers, known. The asymptotic formula is an approximation of the leading term within an asymptotic expansion formulated by ramanujan. Partitions Asymptotic Formulas.
From www.youtube.com
Asymptotic Notation 5 Limit Theorem YouTube Partitions Asymptotic Formulas Let s a;b = fan + b : The asymptotic formula for partitions provides a way to estimate the number of ways an integer can be expressed as the sum of positive integers, known. Let pa(n) denote the number of partitions of n with parts belonging to a. , ak} be a set of k relatively prime positive integers. Asymptotics. Partitions Asymptotic Formulas.
From www.researchgate.net
(PDF) Asymptotic formulas for integer partitions within the approach of Partitions Asymptotic Formulas The asymptotic formula is an approximation of the leading term within an asymptotic expansion formulated by ramanujan and hardy: N 0gwhere n is an integer. A partition of an integer n n is a way of writing n n as a sum of integers. Let s a;b = fan + b : Asymptotics of partition functions daniel m. Let pa(n). Partitions Asymptotic Formulas.
From www.studocu.com
Mindmap Asymptotes Of Rational Functions Vertical Horizontal Slant ÿ Partitions Asymptotic Formulas Let p a;b(n) denote the number of. The asymptotic formula for partitions provides a way to estimate the number of ways an integer can be expressed as the sum of positive integers, known. , ak} be a set of k relatively prime positive integers. Asymptotics of partition functions daniel m. A partition of an integer n n is a way. Partitions Asymptotic Formulas.
From www.researchgate.net
(PDF) An Asymptotic Formula for Cayley's Double Partition Function p(2;n) Partitions Asymptotic Formulas The asymptotic formula for partitions provides a way to estimate the number of ways an integer can be expressed as the sum of positive integers, known. Let p a;b(n) denote the number of. Let pa(n) denote the number of partitions of n with parts belonging to a. N 0gwhere n is an integer. Let s a;b = fan + b. Partitions Asymptotic Formulas.
From mungfali.com
Horizontal Asymptote Chart Partitions Asymptotic Formulas Let pa(n) denote the number of partitions of n with parts belonging to a. Asymptotics of partition functions daniel m. The asymptotic formula for partitions provides a way to estimate the number of ways an integer can be expressed as the sum of positive integers, known. The asymptotic formula is an approximation of the leading term within an asymptotic expansion. Partitions Asymptotic Formulas.
From www.researchgate.net
An asymptotic formula for the logarithm of generalized partition Partitions Asymptotic Formulas The asymptotic formula for partitions provides a way to estimate the number of ways an integer can be expressed as the sum of positive integers, known. Demystifying the asymptotic expression for the partition function. Let s a;b = fan + b : A partition of an integer n n is a way of writing n n as a sum of. Partitions Asymptotic Formulas.
From www.researchgate.net
(PDF) Asymptotic behaviour of the partition function Partitions Asymptotic Formulas N 0gwhere n is an integer. , ak} be a set of k relatively prime positive integers. The asymptotic formula is an approximation of the leading term within an asymptotic expansion formulated by ramanujan and hardy: Let a = {a1, a2,. A partition of an integer n n is a way of writing n n as a sum of integers.. Partitions Asymptotic Formulas.
From www.wikihow.com
How to Find the Equations of the Asymptotes of a Hyperbola Partitions Asymptotic Formulas Let pa(n) denote the number of partitions of n with parts belonging to a. Let a = {a1, a2,. Asymptotics of partition functions daniel m. Let s a;b = fan + b : The asymptotic formula is an approximation of the leading term within an asymptotic expansion formulated by ramanujan and hardy: The asymptotic formula for partitions provides a way. Partitions Asymptotic Formulas.
From www.cuemath.com
What is asymptote formula? Examples Partitions Asymptotic Formulas A partition of an integer n n is a way of writing n n as a sum of integers. Let s a;b = fan + b : Asymptotics of partition functions daniel m. , ak} be a set of k relatively prime positive integers. Let pa(n) denote the number of partitions of n with parts belonging to a. Demystifying the. Partitions Asymptotic Formulas.
From londmathsoc.onlinelibrary.wiley.com
Asymptotic Partition Formulae (II) Weighted Partitions Wright 1934 Partitions Asymptotic Formulas A partition of an integer n n is a way of writing n n as a sum of integers. N 0gwhere n is an integer. Let s a;b = fan + b : Let pa(n) denote the number of partitions of n with parts belonging to a. Asymptotics of partition functions daniel m. Demystifying the asymptotic expression for the partition. Partitions Asymptotic Formulas.
From link.springer.com
Asymptotic expansions for partitions generated by infinite products Partitions Asymptotic Formulas N 0gwhere n is an integer. Let pa(n) denote the number of partitions of n with parts belonging to a. Asymptotics of partition functions daniel m. A partition of an integer n n is a way of writing n n as a sum of integers. The asymptotic formula is an approximation of the leading term within an asymptotic expansion formulated. Partitions Asymptotic Formulas.
From travorlzh.github.io
Asymptotic theory of integer partitions Travor's Home Page Partitions Asymptotic Formulas The asymptotic formula is an approximation of the leading term within an asymptotic expansion formulated by ramanujan and hardy: , ak} be a set of k relatively prime positive integers. Demystifying the asymptotic expression for the partition function. Let a = {a1, a2,. Asymptotics of partition functions daniel m. A partition of an integer n n is a way of. Partitions Asymptotic Formulas.
From www.researchgate.net
(PDF) An Asymptotic Formula for(1 + 1/x) x Based on the Partition Function Partitions Asymptotic Formulas The asymptotic formula is an approximation of the leading term within an asymptotic expansion formulated by ramanujan and hardy: , ak} be a set of k relatively prime positive integers. The asymptotic formula for partitions provides a way to estimate the number of ways an integer can be expressed as the sum of positive integers, known. Let s a;b =. Partitions Asymptotic Formulas.
From www.researchgate.net
(PDF) On the Asymptotic Formula for the Number of Plane Partitions of Partitions Asymptotic Formulas Let p a;b(n) denote the number of. Asymptotics of partition functions daniel m. The asymptotic formula is an approximation of the leading term within an asymptotic expansion formulated by ramanujan and hardy: , ak} be a set of k relatively prime positive integers. Let s a;b = fan + b : A partition of an integer n n is a. Partitions Asymptotic Formulas.
From www.researchgate.net
The asymptotic partition Λ Download Scientific Diagram Partitions Asymptotic Formulas Let pa(n) denote the number of partitions of n with parts belonging to a. The asymptotic formula is an approximation of the leading term within an asymptotic expansion formulated by ramanujan and hardy: Let a = {a1, a2,. Let s a;b = fan + b : The asymptotic formula for partitions provides a way to estimate the number of ways. Partitions Asymptotic Formulas.