Temperature Change Differential Equation . The quantitative relationship between heat transfer and temperature change contains all three factors: The heat equation describes how heat diffuses through a medium over time. • putting these together, we obtain the differential equation y0 = α(y. Newton's law of cooling states that the temperature of a body changes at a rate proportional to the difference in temperature. Q = mcδt, where q is the symbol for heat transfer, m is the mass of. In a small change in time $t$ the temperature change of the body $t(t)$ is proportional to the change in the amount of time $t$ and to the to. Temperature and the ambient temperature is then y(t) − a. It is formulated considering a small volume element. In this section we will do a partial derivation of the heat equation that can be solved to give the temperature in a one dimensional.
from www.theengineeringprojects.com
Newton's law of cooling states that the temperature of a body changes at a rate proportional to the difference in temperature. Q = mcδt, where q is the symbol for heat transfer, m is the mass of. In a small change in time $t$ the temperature change of the body $t(t)$ is proportional to the change in the amount of time $t$ and to the to. Temperature and the ambient temperature is then y(t) − a. In this section we will do a partial derivation of the heat equation that can be solved to give the temperature in a one dimensional. It is formulated considering a small volume element. • putting these together, we obtain the differential equation y0 = α(y. The heat equation describes how heat diffuses through a medium over time. The quantitative relationship between heat transfer and temperature change contains all three factors:
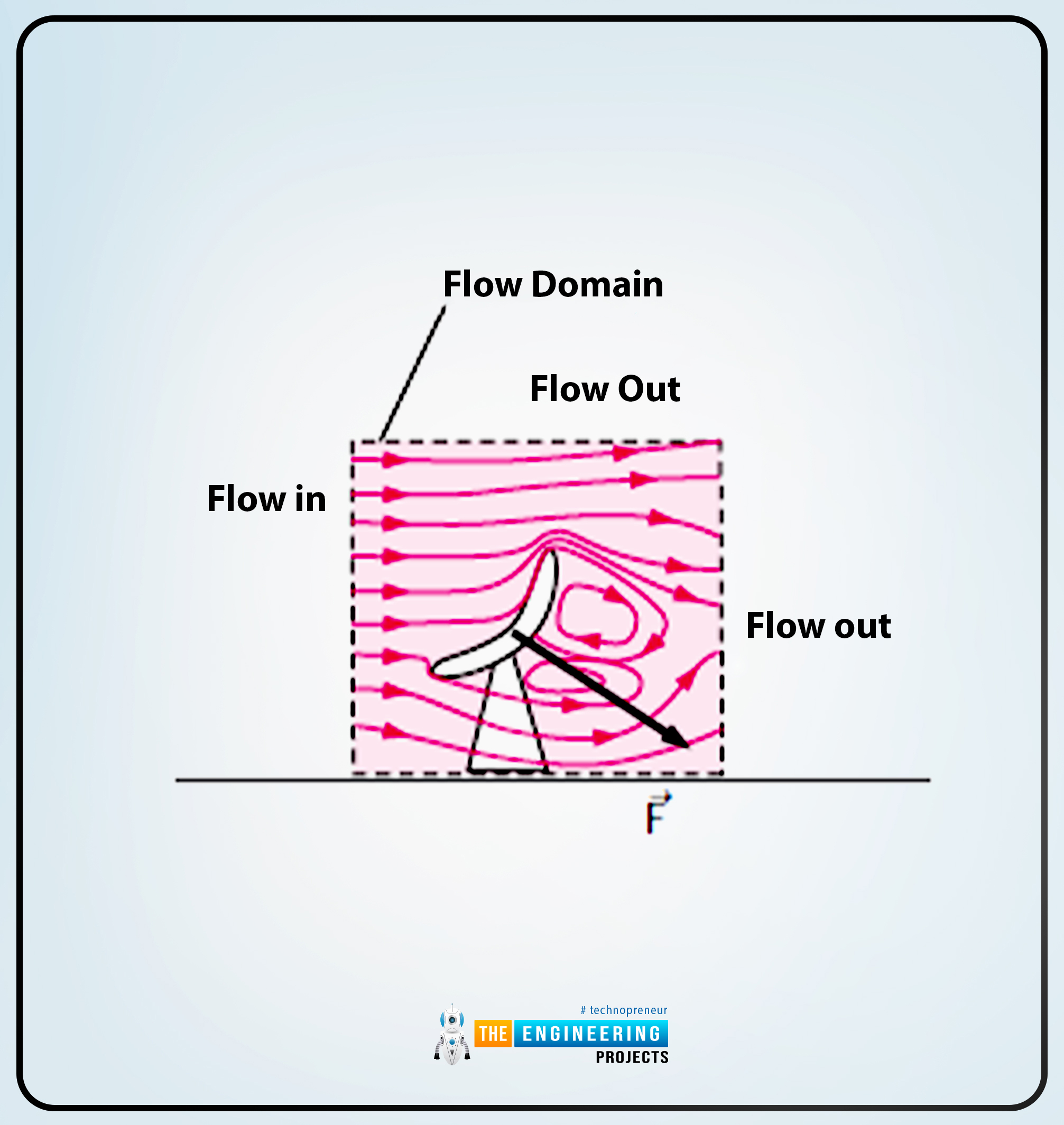
Differential Analysis of Fluid Flow The Engineering Projects
Temperature Change Differential Equation The heat equation describes how heat diffuses through a medium over time. Newton's law of cooling states that the temperature of a body changes at a rate proportional to the difference in temperature. Q = mcδt, where q is the symbol for heat transfer, m is the mass of. • putting these together, we obtain the differential equation y0 = α(y. In this section we will do a partial derivation of the heat equation that can be solved to give the temperature in a one dimensional. Temperature and the ambient temperature is then y(t) − a. In a small change in time $t$ the temperature change of the body $t(t)$ is proportional to the change in the amount of time $t$ and to the to. The quantitative relationship between heat transfer and temperature change contains all three factors: It is formulated considering a small volume element. The heat equation describes how heat diffuses through a medium over time.
From www.chegg.com
Solved (1 point) Consider the partial differential equation Temperature Change Differential Equation Q = mcδt, where q is the symbol for heat transfer, m is the mass of. It is formulated considering a small volume element. The quantitative relationship between heat transfer and temperature change contains all three factors: • putting these together, we obtain the differential equation y0 = α(y. Newton's law of cooling states that the temperature of a body. Temperature Change Differential Equation.
From www.theengineeringprojects.com
Differential Analysis of Fluid Flow The Engineering Projects Temperature Change Differential Equation In this section we will do a partial derivation of the heat equation that can be solved to give the temperature in a one dimensional. The quantitative relationship between heat transfer and temperature change contains all three factors: Temperature and the ambient temperature is then y(t) − a. Newton's law of cooling states that the temperature of a body changes. Temperature Change Differential Equation.
From courses.lumenlearning.com
Temperature Change and Heat Capacity Physics Temperature Change Differential Equation In this section we will do a partial derivation of the heat equation that can be solved to give the temperature in a one dimensional. • putting these together, we obtain the differential equation y0 = α(y. Q = mcδt, where q is the symbol for heat transfer, m is the mass of. In a small change in time $t$. Temperature Change Differential Equation.
From blog.1000bulbs.com
Temperature Differential (DIF) Technique — 1000Bulbs Blog Temperature Change Differential Equation The heat equation describes how heat diffuses through a medium over time. Temperature and the ambient temperature is then y(t) − a. It is formulated considering a small volume element. In a small change in time $t$ the temperature change of the body $t(t)$ is proportional to the change in the amount of time $t$ and to the to. Newton's. Temperature Change Differential Equation.
From www.chegg.com
+ Solve the 2D heat transfer problem of elliptic Temperature Change Differential Equation The quantitative relationship between heat transfer and temperature change contains all three factors: The heat equation describes how heat diffuses through a medium over time. Q = mcδt, where q is the symbol for heat transfer, m is the mass of. • putting these together, we obtain the differential equation y0 = α(y. In this section we will do a. Temperature Change Differential Equation.
From www.youtube.com
Heat Transfer L12 p1 Finite Difference Heat Equation YouTube Temperature Change Differential Equation In this section we will do a partial derivation of the heat equation that can be solved to give the temperature in a one dimensional. Q = mcδt, where q is the symbol for heat transfer, m is the mass of. Newton's law of cooling states that the temperature of a body changes at a rate proportional to the difference. Temperature Change Differential Equation.
From www.instpedia.com
Flow Temperature Change Differential Equation The quantitative relationship between heat transfer and temperature change contains all three factors: In this section we will do a partial derivation of the heat equation that can be solved to give the temperature in a one dimensional. The heat equation describes how heat diffuses through a medium over time. Q = mcδt, where q is the symbol for heat. Temperature Change Differential Equation.
From www.chegg.com
Solved Consider the partial differential equation for heat Temperature Change Differential Equation Newton's law of cooling states that the temperature of a body changes at a rate proportional to the difference in temperature. The quantitative relationship between heat transfer and temperature change contains all three factors: It is formulated considering a small volume element. In a small change in time $t$ the temperature change of the body $t(t)$ is proportional to the. Temperature Change Differential Equation.
From www.tessshebaylo.com
Equation For Heat Energy Absorbed Tessshebaylo Temperature Change Differential Equation Q = mcδt, where q is the symbol for heat transfer, m is the mass of. It is formulated considering a small volume element. The quantitative relationship between heat transfer and temperature change contains all three factors: The heat equation describes how heat diffuses through a medium over time. • putting these together, we obtain the differential equation y0 =. Temperature Change Differential Equation.
From www.slideserve.com
PPT Newton’s Law of Cooling PowerPoint Presentation, free download Temperature Change Differential Equation In a small change in time $t$ the temperature change of the body $t(t)$ is proportional to the change in the amount of time $t$ and to the to. Q = mcδt, where q is the symbol for heat transfer, m is the mass of. The heat equation describes how heat diffuses through a medium over time. The quantitative relationship. Temperature Change Differential Equation.
From www.sharetechnote.com
Engineering Math ShareTechnote Temperature Change Differential Equation In a small change in time $t$ the temperature change of the body $t(t)$ is proportional to the change in the amount of time $t$ and to the to. It is formulated considering a small volume element. Newton's law of cooling states that the temperature of a body changes at a rate proportional to the difference in temperature. Q =. Temperature Change Differential Equation.
From www.youtube.com
SE Chap 8 Differential Rate Equation YouTube Temperature Change Differential Equation The quantitative relationship between heat transfer and temperature change contains all three factors: Newton's law of cooling states that the temperature of a body changes at a rate proportional to the difference in temperature. In this section we will do a partial derivation of the heat equation that can be solved to give the temperature in a one dimensional. The. Temperature Change Differential Equation.
From www.chegg.com
Solved 4. Equation gives the effect of temperature on the Temperature Change Differential Equation Newton's law of cooling states that the temperature of a body changes at a rate proportional to the difference in temperature. • putting these together, we obtain the differential equation y0 = α(y. The heat equation describes how heat diffuses through a medium over time. Q = mcδt, where q is the symbol for heat transfer, m is the mass. Temperature Change Differential Equation.
From www.youtube.com
Applications of First Order Differential Equations Newton's Law of Temperature Change Differential Equation • putting these together, we obtain the differential equation y0 = α(y. Q = mcδt, where q is the symbol for heat transfer, m is the mass of. It is formulated considering a small volume element. Newton's law of cooling states that the temperature of a body changes at a rate proportional to the difference in temperature. In a small. Temperature Change Differential Equation.
From www.chegg.com
Solved Consider the partial differential equation for heat Temperature Change Differential Equation In this section we will do a partial derivation of the heat equation that can be solved to give the temperature in a one dimensional. Temperature and the ambient temperature is then y(t) − a. Newton's law of cooling states that the temperature of a body changes at a rate proportional to the difference in temperature. It is formulated considering. Temperature Change Differential Equation.
From www.slideserve.com
PPT Energy, Power and Climate Change PowerPoint Presentation, free Temperature Change Differential Equation The quantitative relationship between heat transfer and temperature change contains all three factors: In a small change in time $t$ the temperature change of the body $t(t)$ is proportional to the change in the amount of time $t$ and to the to. The heat equation describes how heat diffuses through a medium over time. Q = mcδt, where q is. Temperature Change Differential Equation.
From www.youtube.com
Newton's Law of Cooling Calculus, Example Problems, Differential Temperature Change Differential Equation In this section we will do a partial derivation of the heat equation that can be solved to give the temperature in a one dimensional. The quantitative relationship between heat transfer and temperature change contains all three factors: It is formulated considering a small volume element. • putting these together, we obtain the differential equation y0 = α(y. In a. Temperature Change Differential Equation.
From www.chegg.com
Solved Write a differential equation that fits the physical Temperature Change Differential Equation Q = mcδt, where q is the symbol for heat transfer, m is the mass of. In this section we will do a partial derivation of the heat equation that can be solved to give the temperature in a one dimensional. The quantitative relationship between heat transfer and temperature change contains all three factors: Temperature and the ambient temperature is. Temperature Change Differential Equation.
From physics.stackexchange.com
thermodynamics Derivation of heat capacity at constant pressure and Temperature Change Differential Equation Newton's law of cooling states that the temperature of a body changes at a rate proportional to the difference in temperature. In this section we will do a partial derivation of the heat equation that can be solved to give the temperature in a one dimensional. Temperature and the ambient temperature is then y(t) − a. The heat equation describes. Temperature Change Differential Equation.
From www.chegg.com
Solved Consider the partial differential equation for heat Temperature Change Differential Equation In a small change in time $t$ the temperature change of the body $t(t)$ is proportional to the change in the amount of time $t$ and to the to. In this section we will do a partial derivation of the heat equation that can be solved to give the temperature in a one dimensional. It is formulated considering a small. Temperature Change Differential Equation.
From www.numerade.com
SOLVED (a) A refrigerated object is placed in a 68°F room. Write the Temperature Change Differential Equation It is formulated considering a small volume element. Newton's law of cooling states that the temperature of a body changes at a rate proportional to the difference in temperature. Q = mcδt, where q is the symbol for heat transfer, m is the mass of. In this section we will do a partial derivation of the heat equation that can. Temperature Change Differential Equation.
From www.numerade.com
SOLVED Newton's law of cooling states that the temperature of an Temperature Change Differential Equation The heat equation describes how heat diffuses through a medium over time. It is formulated considering a small volume element. Newton's law of cooling states that the temperature of a body changes at a rate proportional to the difference in temperature. In this section we will do a partial derivation of the heat equation that can be solved to give. Temperature Change Differential Equation.
From ar.inspiredpencil.com
Heat Transfer Equation Temperature Change Differential Equation The quantitative relationship between heat transfer and temperature change contains all three factors: Temperature and the ambient temperature is then y(t) − a. Newton's law of cooling states that the temperature of a body changes at a rate proportional to the difference in temperature. It is formulated considering a small volume element. In this section we will do a partial. Temperature Change Differential Equation.
From www.pinterest.co.uk
A mathematical derivation of the equations relating the pressure Temperature Change Differential Equation Newton's law of cooling states that the temperature of a body changes at a rate proportional to the difference in temperature. In this section we will do a partial derivation of the heat equation that can be solved to give the temperature in a one dimensional. Q = mcδt, where q is the symbol for heat transfer, m is the. Temperature Change Differential Equation.
From www.youtube.com
Calculate Gibbs Free Energy Change for a Reaction at Elevated Temperature Change Differential Equation Q = mcδt, where q is the symbol for heat transfer, m is the mass of. In a small change in time $t$ the temperature change of the body $t(t)$ is proportional to the change in the amount of time $t$ and to the to. It is formulated considering a small volume element. The quantitative relationship between heat transfer and. Temperature Change Differential Equation.
From peachyfileson.cf
Differential equations by m d raisinghania Temperature Change Differential Equation Temperature and the ambient temperature is then y(t) − a. The quantitative relationship between heat transfer and temperature change contains all three factors: It is formulated considering a small volume element. Q = mcδt, where q is the symbol for heat transfer, m is the mass of. In a small change in time $t$ the temperature change of the body. Temperature Change Differential Equation.
From www.youtube.com
change in temperature calculations YouTube Temperature Change Differential Equation The heat equation describes how heat diffuses through a medium over time. In a small change in time $t$ the temperature change of the body $t(t)$ is proportional to the change in the amount of time $t$ and to the to. • putting these together, we obtain the differential equation y0 = α(y. It is formulated considering a small volume. Temperature Change Differential Equation.
From www.chegg.com
Solved Consider the heat equation in a twodimensional Temperature Change Differential Equation In this section we will do a partial derivation of the heat equation that can be solved to give the temperature in a one dimensional. In a small change in time $t$ the temperature change of the body $t(t)$ is proportional to the change in the amount of time $t$ and to the to. It is formulated considering a small. Temperature Change Differential Equation.
From www.chegg.com
Solved The differential equation below models the Temperature Change Differential Equation In a small change in time $t$ the temperature change of the body $t(t)$ is proportional to the change in the amount of time $t$ and to the to. • putting these together, we obtain the differential equation y0 = α(y. In this section we will do a partial derivation of the heat equation that can be solved to give. Temperature Change Differential Equation.
From studylib.net
Heat Equation Temperature Change Differential Equation It is formulated considering a small volume element. The heat equation describes how heat diffuses through a medium over time. Newton's law of cooling states that the temperature of a body changes at a rate proportional to the difference in temperature. Q = mcδt, where q is the symbol for heat transfer, m is the mass of. In this section. Temperature Change Differential Equation.
From www.slideserve.com
PPT Differential Equations PowerPoint Presentation, free download Temperature Change Differential Equation • putting these together, we obtain the differential equation y0 = α(y. Q = mcδt, where q is the symbol for heat transfer, m is the mass of. Newton's law of cooling states that the temperature of a body changes at a rate proportional to the difference in temperature. It is formulated considering a small volume element. In this section. Temperature Change Differential Equation.
From www.chegg.com
Solved Consider the partial differential equation for heat Temperature Change Differential Equation Q = mcδt, where q is the symbol for heat transfer, m is the mass of. The heat equation describes how heat diffuses through a medium over time. Temperature and the ambient temperature is then y(t) − a. In a small change in time $t$ the temperature change of the body $t(t)$ is proportional to the change in the amount. Temperature Change Differential Equation.
From www.slideserve.com
PPT SECTION 1 HEAT TRANSFER ANALYSIS PowerPoint Presentation, free Temperature Change Differential Equation The quantitative relationship between heat transfer and temperature change contains all three factors: Newton's law of cooling states that the temperature of a body changes at a rate proportional to the difference in temperature. • putting these together, we obtain the differential equation y0 = α(y. In this section we will do a partial derivation of the heat equation that. Temperature Change Differential Equation.
From dylanewalane.blogspot.com
Log Mean Temperature Difference Formula DylanewaLane Temperature Change Differential Equation Newton's law of cooling states that the temperature of a body changes at a rate proportional to the difference in temperature. In a small change in time $t$ the temperature change of the body $t(t)$ is proportional to the change in the amount of time $t$ and to the to. It is formulated considering a small volume element. • putting. Temperature Change Differential Equation.
From math.stackexchange.com
calculus Differential equations temperature change and room Temperature Change Differential Equation • putting these together, we obtain the differential equation y0 = α(y. The quantitative relationship between heat transfer and temperature change contains all three factors: In this section we will do a partial derivation of the heat equation that can be solved to give the temperature in a one dimensional. Newton's law of cooling states that the temperature of a. Temperature Change Differential Equation.