Moment Of Inertia In Z Axis . Apply the parallel axis theorem to find the moment of inertia. Apply the parallel axis theorem to find the moment of inertia. the moment of inertia about the z axis is the sum of the moments of inertia about the other two axes. i am wanting to find i, the moment of inertia about the z axis of the region that is bounded by the paraboloid $z=x^{2}+y^{2}$ and the. It is easy to prove. calculate the moment of inertia for uniformly shaped, rigid bodies; zz are called moments of inertia with respect to the x, y and z axis, respectively, and are given by i xx = (y 2 + z 2) dm, i yy = (x 2 +. All axes pass through the centre of mass. in following sections we will use the integral definitions of moment of inertia (10.1.3) to find the moments of inertia of five common shapes: the moment of inertia about each axis represents the shapes resistance to a moment applied about that respective axis. Calculate the moment of inertia for uniformly shaped, rigid bodies.
from www.chegg.com
Apply the parallel axis theorem to find the moment of inertia. zz are called moments of inertia with respect to the x, y and z axis, respectively, and are given by i xx = (y 2 + z 2) dm, i yy = (x 2 +. It is easy to prove. i am wanting to find i, the moment of inertia about the z axis of the region that is bounded by the paraboloid $z=x^{2}+y^{2}$ and the. the moment of inertia about the z axis is the sum of the moments of inertia about the other two axes. Apply the parallel axis theorem to find the moment of inertia. the moment of inertia about each axis represents the shapes resistance to a moment applied about that respective axis. Calculate the moment of inertia for uniformly shaped, rigid bodies. calculate the moment of inertia for uniformly shaped, rigid bodies; in following sections we will use the integral definitions of moment of inertia (10.1.3) to find the moments of inertia of five common shapes:
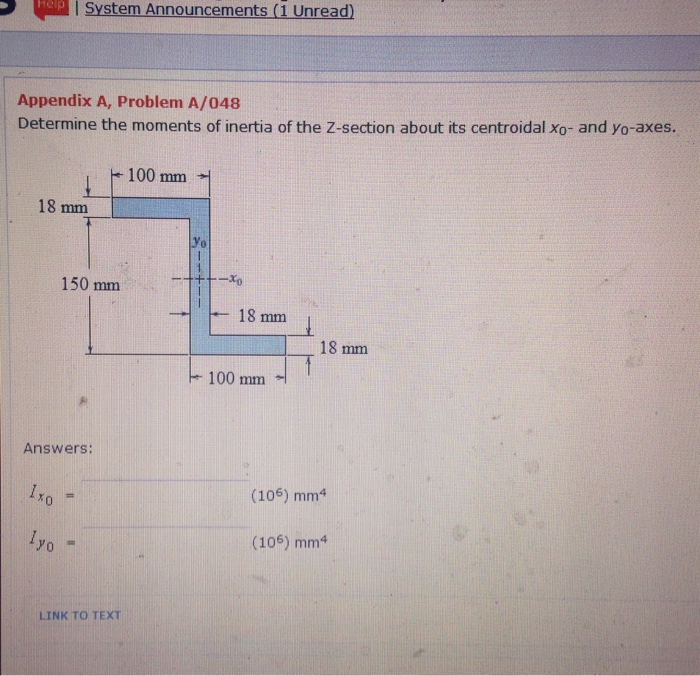
Solved Determine the moments of inertia of the zsection
Moment Of Inertia In Z Axis Calculate the moment of inertia for uniformly shaped, rigid bodies. in following sections we will use the integral definitions of moment of inertia (10.1.3) to find the moments of inertia of five common shapes: i am wanting to find i, the moment of inertia about the z axis of the region that is bounded by the paraboloid $z=x^{2}+y^{2}$ and the. All axes pass through the centre of mass. It is easy to prove. the moment of inertia about each axis represents the shapes resistance to a moment applied about that respective axis. Apply the parallel axis theorem to find the moment of inertia. the moment of inertia about the z axis is the sum of the moments of inertia about the other two axes. Calculate the moment of inertia for uniformly shaped, rigid bodies. zz are called moments of inertia with respect to the x, y and z axis, respectively, and are given by i xx = (y 2 + z 2) dm, i yy = (x 2 +. Apply the parallel axis theorem to find the moment of inertia. calculate the moment of inertia for uniformly shaped, rigid bodies;
From www.chegg.com
Solved Determine the moments of inertia of the Zsection Moment Of Inertia In Z Axis the moment of inertia about the z axis is the sum of the moments of inertia about the other two axes. i am wanting to find i, the moment of inertia about the z axis of the region that is bounded by the paraboloid $z=x^{2}+y^{2}$ and the. zz are called moments of inertia with respect to the. Moment Of Inertia In Z Axis.
From www.chegg.com
Solved Determine the moments of inertia of the Zsection Moment Of Inertia In Z Axis in following sections we will use the integral definitions of moment of inertia (10.1.3) to find the moments of inertia of five common shapes: All axes pass through the centre of mass. zz are called moments of inertia with respect to the x, y and z axis, respectively, and are given by i xx = (y 2 +. Moment Of Inertia In Z Axis.
From itchol.com
Moment of inertia formulas for different shapes Structural Basics (2023) Moment Of Inertia In Z Axis the moment of inertia about each axis represents the shapes resistance to a moment applied about that respective axis. in following sections we will use the integral definitions of moment of inertia (10.1.3) to find the moments of inertia of five common shapes: zz are called moments of inertia with respect to the x, y and z. Moment Of Inertia In Z Axis.
From www.chegg.com
Solved Determine the mass moment of inertia about the zaxis Moment Of Inertia In Z Axis zz are called moments of inertia with respect to the x, y and z axis, respectively, and are given by i xx = (y 2 + z 2) dm, i yy = (x 2 +. the moment of inertia about each axis represents the shapes resistance to a moment applied about that respective axis. Apply the parallel axis. Moment Of Inertia In Z Axis.
From mungfali.com
Moment Of Inertia Cross Section Moment Of Inertia In Z Axis calculate the moment of inertia for uniformly shaped, rigid bodies; zz are called moments of inertia with respect to the x, y and z axis, respectively, and are given by i xx = (y 2 + z 2) dm, i yy = (x 2 +. Calculate the moment of inertia for uniformly shaped, rigid bodies. Apply the parallel. Moment Of Inertia In Z Axis.
From byjus.com
Moment Of Inertia Formula, Unit, Dimension And Solved Examples Moment Of Inertia In Z Axis in following sections we will use the integral definitions of moment of inertia (10.1.3) to find the moments of inertia of five common shapes: Apply the parallel axis theorem to find the moment of inertia. It is easy to prove. the moment of inertia about each axis represents the shapes resistance to a moment applied about that respective. Moment Of Inertia In Z Axis.
From www.doubtnut.com
Doubt Solutions Maths, Science, CBSE, NCERT, IIT JEE, NEET Moment Of Inertia In Z Axis Apply the parallel axis theorem to find the moment of inertia. the moment of inertia about each axis represents the shapes resistance to a moment applied about that respective axis. Calculate the moment of inertia for uniformly shaped, rigid bodies. calculate the moment of inertia for uniformly shaped, rigid bodies; i am wanting to find i, the. Moment Of Inertia In Z Axis.
From es.vecteezy.com
ejemplos de momento de inercia para esfera sólida, capa esférica, losa Moment Of Inertia In Z Axis calculate the moment of inertia for uniformly shaped, rigid bodies; in following sections we will use the integral definitions of moment of inertia (10.1.3) to find the moments of inertia of five common shapes: Apply the parallel axis theorem to find the moment of inertia. i am wanting to find i, the moment of inertia about the. Moment Of Inertia In Z Axis.
From web2.ph.utexas.edu
Moments of Inertia Moment Of Inertia In Z Axis the moment of inertia about each axis represents the shapes resistance to a moment applied about that respective axis. All axes pass through the centre of mass. Calculate the moment of inertia for uniformly shaped, rigid bodies. in following sections we will use the integral definitions of moment of inertia (10.1.3) to find the moments of inertia of. Moment Of Inertia In Z Axis.
From www.youtube.com
Problem on Centroid and Moment of Inertia of Z section YouTube Moment Of Inertia In Z Axis calculate the moment of inertia for uniformly shaped, rigid bodies; zz are called moments of inertia with respect to the x, y and z axis, respectively, and are given by i xx = (y 2 + z 2) dm, i yy = (x 2 +. All axes pass through the centre of mass. Apply the parallel axis theorem. Moment Of Inertia In Z Axis.
From mungfali.com
Moment Of Inertia Common Shapes Moment Of Inertia In Z Axis Calculate the moment of inertia for uniformly shaped, rigid bodies. calculate the moment of inertia for uniformly shaped, rigid bodies; All axes pass through the centre of mass. It is easy to prove. the moment of inertia about each axis represents the shapes resistance to a moment applied about that respective axis. the moment of inertia about. Moment Of Inertia In Z Axis.
From www.chegg.com
Solved Determine the moments of inertia of the zsection Moment Of Inertia In Z Axis the moment of inertia about each axis represents the shapes resistance to a moment applied about that respective axis. All axes pass through the centre of mass. Calculate the moment of inertia for uniformly shaped, rigid bodies. Apply the parallel axis theorem to find the moment of inertia. It is easy to prove. the moment of inertia about. Moment Of Inertia In Z Axis.
From www.chegg.com
Solved Determine the mass moment of inertia of the solid Moment Of Inertia In Z Axis Apply the parallel axis theorem to find the moment of inertia. the moment of inertia about the z axis is the sum of the moments of inertia about the other two axes. i am wanting to find i, the moment of inertia about the z axis of the region that is bounded by the paraboloid $z=x^{2}+y^{2}$ and the.. Moment Of Inertia In Z Axis.
From pressbooks.library.upei.ca
7.4 Mass Moment of Inertia Engineering Mechanics Statics Moment Of Inertia In Z Axis Calculate the moment of inertia for uniformly shaped, rigid bodies. the moment of inertia about the z axis is the sum of the moments of inertia about the other two axes. calculate the moment of inertia for uniformly shaped, rigid bodies; Apply the parallel axis theorem to find the moment of inertia. in following sections we will. Moment Of Inertia In Z Axis.
From www.youtube.com
Engineering Mechanics Statics Theory Moment of Inertia YouTube Moment Of Inertia In Z Axis i am wanting to find i, the moment of inertia about the z axis of the region that is bounded by the paraboloid $z=x^{2}+y^{2}$ and the. Apply the parallel axis theorem to find the moment of inertia. All axes pass through the centre of mass. Apply the parallel axis theorem to find the moment of inertia. in following. Moment Of Inertia In Z Axis.
From www.youtube.com
Principal Moments of Inertia and Principal Axes YouTube Moment Of Inertia In Z Axis Apply the parallel axis theorem to find the moment of inertia. calculate the moment of inertia for uniformly shaped, rigid bodies; Apply the parallel axis theorem to find the moment of inertia. Calculate the moment of inertia for uniformly shaped, rigid bodies. in following sections we will use the integral definitions of moment of inertia (10.1.3) to find. Moment Of Inertia In Z Axis.
From www.chegg.com
Solved Determine the mass moment of inertia in each axis. Moment Of Inertia In Z Axis zz are called moments of inertia with respect to the x, y and z axis, respectively, and are given by i xx = (y 2 + z 2) dm, i yy = (x 2 +. the moment of inertia about each axis represents the shapes resistance to a moment applied about that respective axis. i am wanting. Moment Of Inertia In Z Axis.
From engineerexcel.com
Parallel Axis Theorem for Area Moment of Inertia EngineerExcel Moment Of Inertia In Z Axis Calculate the moment of inertia for uniformly shaped, rigid bodies. calculate the moment of inertia for uniformly shaped, rigid bodies; It is easy to prove. All axes pass through the centre of mass. the moment of inertia about each axis represents the shapes resistance to a moment applied about that respective axis. i am wanting to find. Moment Of Inertia In Z Axis.
From www.coursehero.com
[Solved] . Determine the moments of inertia of the Zsection about its Moment Of Inertia In Z Axis Calculate the moment of inertia for uniformly shaped, rigid bodies. zz are called moments of inertia with respect to the x, y and z axis, respectively, and are given by i xx = (y 2 + z 2) dm, i yy = (x 2 +. i am wanting to find i, the moment of inertia about the z. Moment Of Inertia In Z Axis.
From www.youtube.com
The moment of inertia tensor Chapter 25 Classical Mechanics 2 YouTube Moment Of Inertia In Z Axis Apply the parallel axis theorem to find the moment of inertia. zz are called moments of inertia with respect to the x, y and z axis, respectively, and are given by i xx = (y 2 + z 2) dm, i yy = (x 2 +. Calculate the moment of inertia for uniformly shaped, rigid bodies. i am. Moment Of Inertia In Z Axis.
From www.sciencefacts.net
Moment of Inertia Definition, Formula, Examples, & Table Moment Of Inertia In Z Axis Apply the parallel axis theorem to find the moment of inertia. calculate the moment of inertia for uniformly shaped, rigid bodies; in following sections we will use the integral definitions of moment of inertia (10.1.3) to find the moments of inertia of five common shapes: zz are called moments of inertia with respect to the x, y. Moment Of Inertia In Z Axis.
From www.chegg.com
Solved Determine the moments of inertia of the Zsection Moment Of Inertia In Z Axis in following sections we will use the integral definitions of moment of inertia (10.1.3) to find the moments of inertia of five common shapes: Calculate the moment of inertia for uniformly shaped, rigid bodies. calculate the moment of inertia for uniformly shaped, rigid bodies; zz are called moments of inertia with respect to the x, y and. Moment Of Inertia In Z Axis.
From avantecnica.qualitypoolsboulder.com
How to calculate Moment of Inertia? Formulas and Solved Examples Moment Of Inertia In Z Axis It is easy to prove. Apply the parallel axis theorem to find the moment of inertia. the moment of inertia about the z axis is the sum of the moments of inertia about the other two axes. the moment of inertia about each axis represents the shapes resistance to a moment applied about that respective axis. calculate. Moment Of Inertia In Z Axis.
From www.chegg.com
Solved Calculate the moment of inertia about the zaxis. Moment Of Inertia In Z Axis It is easy to prove. calculate the moment of inertia for uniformly shaped, rigid bodies; zz are called moments of inertia with respect to the x, y and z axis, respectively, and are given by i xx = (y 2 + z 2) dm, i yy = (x 2 +. All axes pass through the centre of mass.. Moment Of Inertia In Z Axis.
From www.youtube.com
Moment of Inertia of an Z Section YouTube Moment Of Inertia In Z Axis Calculate the moment of inertia for uniformly shaped, rigid bodies. the moment of inertia about the z axis is the sum of the moments of inertia about the other two axes. zz are called moments of inertia with respect to the x, y and z axis, respectively, and are given by i xx = (y 2 + z. Moment Of Inertia In Z Axis.
From www.youtube.com
Moment of Inertia by Integration with Identical dA YouTube Moment Of Inertia In Z Axis zz are called moments of inertia with respect to the x, y and z axis, respectively, and are given by i xx = (y 2 + z 2) dm, i yy = (x 2 +. Apply the parallel axis theorem to find the moment of inertia. Calculate the moment of inertia for uniformly shaped, rigid bodies. Apply the parallel. Moment Of Inertia In Z Axis.
From brainly.com
1. Determine the moments of inertia of the Zsection about its Moment Of Inertia In Z Axis the moment of inertia about each axis represents the shapes resistance to a moment applied about that respective axis. Calculate the moment of inertia for uniformly shaped, rigid bodies. the moment of inertia about the z axis is the sum of the moments of inertia about the other two axes. zz are called moments of inertia with. Moment Of Inertia In Z Axis.
From oneclass.com
OneClass Determine the moments of inertia of the Zsection about its Moment Of Inertia In Z Axis Apply the parallel axis theorem to find the moment of inertia. All axes pass through the centre of mass. in following sections we will use the integral definitions of moment of inertia (10.1.3) to find the moments of inertia of five common shapes: zz are called moments of inertia with respect to the x, y and z axis,. Moment Of Inertia In Z Axis.
From www.slideserve.com
PPT Distributed Forces Moments of Inertia PowerPoint Presentation Moment Of Inertia In Z Axis Calculate the moment of inertia for uniformly shaped, rigid bodies. zz are called moments of inertia with respect to the x, y and z axis, respectively, and are given by i xx = (y 2 + z 2) dm, i yy = (x 2 +. All axes pass through the centre of mass. in following sections we will. Moment Of Inertia In Z Axis.
From www.youtube.com
Find the Moment of Inertia about the zaxis of a Solid Using Triple Moment Of Inertia In Z Axis It is easy to prove. calculate the moment of inertia for uniformly shaped, rigid bodies; in following sections we will use the integral definitions of moment of inertia (10.1.3) to find the moments of inertia of five common shapes: zz are called moments of inertia with respect to the x, y and z axis, respectively, and are. Moment Of Inertia In Z Axis.
From www.youtube.com
Moment of Inertia of Rectangular Section Mechanics of Solid Moment Of Inertia In Z Axis i am wanting to find i, the moment of inertia about the z axis of the region that is bounded by the paraboloid $z=x^{2}+y^{2}$ and the. zz are called moments of inertia with respect to the x, y and z axis, respectively, and are given by i xx = (y 2 + z 2) dm, i yy =. Moment Of Inertia In Z Axis.
From tablestudios.weebly.com
Moment of inertia of a circle tablestudios Moment Of Inertia In Z Axis zz are called moments of inertia with respect to the x, y and z axis, respectively, and are given by i xx = (y 2 + z 2) dm, i yy = (x 2 +. Apply the parallel axis theorem to find the moment of inertia. calculate the moment of inertia for uniformly shaped, rigid bodies; It is. Moment Of Inertia In Z Axis.
From byjus.com
how to find the moment of inertia of about an axis which passes at an Moment Of Inertia In Z Axis i am wanting to find i, the moment of inertia about the z axis of the region that is bounded by the paraboloid $z=x^{2}+y^{2}$ and the. zz are called moments of inertia with respect to the x, y and z axis, respectively, and are given by i xx = (y 2 + z 2) dm, i yy =. Moment Of Inertia In Z Axis.
From www.physicsforums.com
Moment of Inertia Elliptical beam Moment Of Inertia In Z Axis the moment of inertia about each axis represents the shapes resistance to a moment applied about that respective axis. All axes pass through the centre of mass. the moment of inertia about the z axis is the sum of the moments of inertia about the other two axes. zz are called moments of inertia with respect to. Moment Of Inertia In Z Axis.
From www.adda247.com
Moment of Inertia Definition, Formula, Examples, Unit, Equations Moment Of Inertia In Z Axis Apply the parallel axis theorem to find the moment of inertia. the moment of inertia about the z axis is the sum of the moments of inertia about the other two axes. It is easy to prove. the moment of inertia about each axis represents the shapes resistance to a moment applied about that respective axis. zz. Moment Of Inertia In Z Axis.