Binomial Distribution Expected Number Of Trials . The expected value of the binomial distribution is its mean. to calculate the mean (expected value) of a binomial distribution b(n,p) you need to multiply the number of trials n by. the binomial probability distribution is excellent for understanding the likelihood of obtaining an exact number of events (x) within a certain number of trials. Next, we require that the number of trials in the experiment be decided before the experiment begins. notation for the binomial: fixed number of trials. \(b =\) binomial probability distribution function \[x \sim b(n, p)\] read this as \(x\) is a random variable with a. if $x$ is the number of successful trials, then assuming independence of trials $x$ has a. the distribution of the number of experiments in which the outcome turns out to be a success is called binomial distribution. expected value of binomial distribution.
from www.geeksforgeeks.org
fixed number of trials. Next, we require that the number of trials in the experiment be decided before the experiment begins. notation for the binomial: to calculate the mean (expected value) of a binomial distribution b(n,p) you need to multiply the number of trials n by. the distribution of the number of experiments in which the outcome turns out to be a success is called binomial distribution. expected value of binomial distribution. the binomial probability distribution is excellent for understanding the likelihood of obtaining an exact number of events (x) within a certain number of trials. \(b =\) binomial probability distribution function \[x \sim b(n, p)\] read this as \(x\) is a random variable with a. if $x$ is the number of successful trials, then assuming independence of trials $x$ has a. The expected value of the binomial distribution is its mean.
Binomial Distribution in Business Statistics Definition, Formula
Binomial Distribution Expected Number Of Trials \(b =\) binomial probability distribution function \[x \sim b(n, p)\] read this as \(x\) is a random variable with a. to calculate the mean (expected value) of a binomial distribution b(n,p) you need to multiply the number of trials n by. The expected value of the binomial distribution is its mean. notation for the binomial: the distribution of the number of experiments in which the outcome turns out to be a success is called binomial distribution. if $x$ is the number of successful trials, then assuming independence of trials $x$ has a. \(b =\) binomial probability distribution function \[x \sim b(n, p)\] read this as \(x\) is a random variable with a. Next, we require that the number of trials in the experiment be decided before the experiment begins. fixed number of trials. expected value of binomial distribution. the binomial probability distribution is excellent for understanding the likelihood of obtaining an exact number of events (x) within a certain number of trials.
From studylib.net
The Mean and Standard Deviation of Binomial Probability Distributions Binomial Distribution Expected Number Of Trials expected value of binomial distribution. Next, we require that the number of trials in the experiment be decided before the experiment begins. notation for the binomial: if $x$ is the number of successful trials, then assuming independence of trials $x$ has a. \(b =\) binomial probability distribution function \[x \sim b(n, p)\] read this as \(x\) is. Binomial Distribution Expected Number Of Trials.
From www.geeksforgeeks.org
Binomial Distribution in Business Statistics Definition, Formula Binomial Distribution Expected Number Of Trials to calculate the mean (expected value) of a binomial distribution b(n,p) you need to multiply the number of trials n by. fixed number of trials. notation for the binomial: the binomial probability distribution is excellent for understanding the likelihood of obtaining an exact number of events (x) within a certain number of trials. expected value. Binomial Distribution Expected Number Of Trials.
From www.chegg.com
Solved Formulas for Binomial Distribution's PMF, CDF, Binomial Distribution Expected Number Of Trials Next, we require that the number of trials in the experiment be decided before the experiment begins. expected value of binomial distribution. fixed number of trials. to calculate the mean (expected value) of a binomial distribution b(n,p) you need to multiply the number of trials n by. if $x$ is the number of successful trials, then. Binomial Distribution Expected Number Of Trials.
From www.slideserve.com
PPT Binomial Distribution PowerPoint Presentation, free download ID Binomial Distribution Expected Number Of Trials the distribution of the number of experiments in which the outcome turns out to be a success is called binomial distribution. expected value of binomial distribution. notation for the binomial: The expected value of the binomial distribution is its mean. to calculate the mean (expected value) of a binomial distribution b(n,p) you need to multiply the. Binomial Distribution Expected Number Of Trials.
From www.technologynetworks.com
The Binomial Test Technology Networks Binomial Distribution Expected Number Of Trials The expected value of the binomial distribution is its mean. the binomial probability distribution is excellent for understanding the likelihood of obtaining an exact number of events (x) within a certain number of trials. the distribution of the number of experiments in which the outcome turns out to be a success is called binomial distribution. expected value. Binomial Distribution Expected Number Of Trials.
From theprobability.netlify.app
Probability Of Binomial Distribution theprobability Binomial Distribution Expected Number Of Trials fixed number of trials. The expected value of the binomial distribution is its mean. the binomial probability distribution is excellent for understanding the likelihood of obtaining an exact number of events (x) within a certain number of trials. \(b =\) binomial probability distribution function \[x \sim b(n, p)\] read this as \(x\) is a random variable with a.. Binomial Distribution Expected Number Of Trials.
From www.slideserve.com
PPT Binomial Probability Distribution 1. The experiment must have a Binomial Distribution Expected Number Of Trials the distribution of the number of experiments in which the outcome turns out to be a success is called binomial distribution. if $x$ is the number of successful trials, then assuming independence of trials $x$ has a. The expected value of the binomial distribution is its mean. notation for the binomial: to calculate the mean (expected. Binomial Distribution Expected Number Of Trials.
From statisticsglobe.com
Binomial Distribution in R (4 Examples) dbinom, pbinom, qbinom, rbinom Binomial Distribution Expected Number Of Trials to calculate the mean (expected value) of a binomial distribution b(n,p) you need to multiply the number of trials n by. notation for the binomial: \(b =\) binomial probability distribution function \[x \sim b(n, p)\] read this as \(x\) is a random variable with a. the distribution of the number of experiments in which the outcome turns. Binomial Distribution Expected Number Of Trials.
From www.slideserve.com
PPT Binomial Probability Distribution 1. The experiment must have a Binomial Distribution Expected Number Of Trials expected value of binomial distribution. to calculate the mean (expected value) of a binomial distribution b(n,p) you need to multiply the number of trials n by. The expected value of the binomial distribution is its mean. \(b =\) binomial probability distribution function \[x \sim b(n, p)\] read this as \(x\) is a random variable with a. the. Binomial Distribution Expected Number Of Trials.
From slideplayer.com
Discrete Random Variables and Probability Distributions ppt download Binomial Distribution Expected Number Of Trials to calculate the mean (expected value) of a binomial distribution b(n,p) you need to multiply the number of trials n by. Next, we require that the number of trials in the experiment be decided before the experiment begins. the binomial probability distribution is excellent for understanding the likelihood of obtaining an exact number of events (x) within a. Binomial Distribution Expected Number Of Trials.
From mungfali.com
Expected Value Of Binomial Distribution Binomial Distribution Expected Number Of Trials if $x$ is the number of successful trials, then assuming independence of trials $x$ has a. \(b =\) binomial probability distribution function \[x \sim b(n, p)\] read this as \(x\) is a random variable with a. to calculate the mean (expected value) of a binomial distribution b(n,p) you need to multiply the number of trials n by. . Binomial Distribution Expected Number Of Trials.
From www.slideserve.com
PPT Binomial Probability Distribution 1. The experiment must have a Binomial Distribution Expected Number Of Trials to calculate the mean (expected value) of a binomial distribution b(n,p) you need to multiply the number of trials n by. expected value of binomial distribution. if $x$ is the number of successful trials, then assuming independence of trials $x$ has a. the binomial probability distribution is excellent for understanding the likelihood of obtaining an exact. Binomial Distribution Expected Number Of Trials.
From www.numerade.com
SOLVED Consider a binomial distribution. if the number of trials is Binomial Distribution Expected Number Of Trials if $x$ is the number of successful trials, then assuming independence of trials $x$ has a. to calculate the mean (expected value) of a binomial distribution b(n,p) you need to multiply the number of trials n by. Next, we require that the number of trials in the experiment be decided before the experiment begins. \(b =\) binomial probability. Binomial Distribution Expected Number Of Trials.
From www.youtube.com
Finding the number of trials in a binomial distribution for a given Binomial Distribution Expected Number Of Trials fixed number of trials. if $x$ is the number of successful trials, then assuming independence of trials $x$ has a. The expected value of the binomial distribution is its mean. the distribution of the number of experiments in which the outcome turns out to be a success is called binomial distribution. the binomial probability distribution is. Binomial Distribution Expected Number Of Trials.
From www.slideserve.com
PPT The Binomial Distribution PowerPoint Presentation, free download Binomial Distribution Expected Number Of Trials the binomial probability distribution is excellent for understanding the likelihood of obtaining an exact number of events (x) within a certain number of trials. \(b =\) binomial probability distribution function \[x \sim b(n, p)\] read this as \(x\) is a random variable with a. The expected value of the binomial distribution is its mean. notation for the binomial:. Binomial Distribution Expected Number Of Trials.
From www.chegg.com
Solved The binomial distribution consists of the Binomial Distribution Expected Number Of Trials if $x$ is the number of successful trials, then assuming independence of trials $x$ has a. notation for the binomial: \(b =\) binomial probability distribution function \[x \sim b(n, p)\] read this as \(x\) is a random variable with a. expected value of binomial distribution. fixed number of trials. The expected value of the binomial distribution. Binomial Distribution Expected Number Of Trials.
From www.qualitygurus.com
Binomial Distribution Quality Gurus Binomial Distribution Expected Number Of Trials the binomial probability distribution is excellent for understanding the likelihood of obtaining an exact number of events (x) within a certain number of trials. The expected value of the binomial distribution is its mean. the distribution of the number of experiments in which the outcome turns out to be a success is called binomial distribution. notation for. Binomial Distribution Expected Number Of Trials.
From www.numerade.com
SOLVEDConsider a binomial distribution with n=10 trials and the Binomial Distribution Expected Number Of Trials The expected value of the binomial distribution is its mean. \(b =\) binomial probability distribution function \[x \sim b(n, p)\] read this as \(x\) is a random variable with a. notation for the binomial: expected value of binomial distribution. fixed number of trials. if $x$ is the number of successful trials, then assuming independence of trials. Binomial Distribution Expected Number Of Trials.
From worker.norushcharge.com
How to Read the Binomial Distribution Table Statology Binomial Distribution Expected Number Of Trials if $x$ is the number of successful trials, then assuming independence of trials $x$ has a. notation for the binomial: the binomial probability distribution is excellent for understanding the likelihood of obtaining an exact number of events (x) within a certain number of trials. expected value of binomial distribution. The expected value of the binomial distribution. Binomial Distribution Expected Number Of Trials.
From www.slideserve.com
PPT Binomial Distribution and Applications PowerPoint Presentation Binomial Distribution Expected Number Of Trials fixed number of trials. Next, we require that the number of trials in the experiment be decided before the experiment begins. the binomial probability distribution is excellent for understanding the likelihood of obtaining an exact number of events (x) within a certain number of trials. \(b =\) binomial probability distribution function \[x \sim b(n, p)\] read this as. Binomial Distribution Expected Number Of Trials.
From medium.com
A Breakdown of Binomial Distribution by Kulle Omer Medium Binomial Distribution Expected Number Of Trials expected value of binomial distribution. The expected value of the binomial distribution is its mean. if $x$ is the number of successful trials, then assuming independence of trials $x$ has a. to calculate the mean (expected value) of a binomial distribution b(n,p) you need to multiply the number of trials n by. the distribution of the. Binomial Distribution Expected Number Of Trials.
From www.nagwa.com
Question Video Calculating the Mean of a Binomial Distribution Nagwa Binomial Distribution Expected Number Of Trials fixed number of trials. \(b =\) binomial probability distribution function \[x \sim b(n, p)\] read this as \(x\) is a random variable with a. Next, we require that the number of trials in the experiment be decided before the experiment begins. The expected value of the binomial distribution is its mean. expected value of binomial distribution. if. Binomial Distribution Expected Number Of Trials.
From articles.outlier.org
Binomial Distribution Meaning & Formula Outlier Binomial Distribution Expected Number Of Trials The expected value of the binomial distribution is its mean. \(b =\) binomial probability distribution function \[x \sim b(n, p)\] read this as \(x\) is a random variable with a. expected value of binomial distribution. notation for the binomial: fixed number of trials. the distribution of the number of experiments in which the outcome turns out. Binomial Distribution Expected Number Of Trials.
From www.statology.org
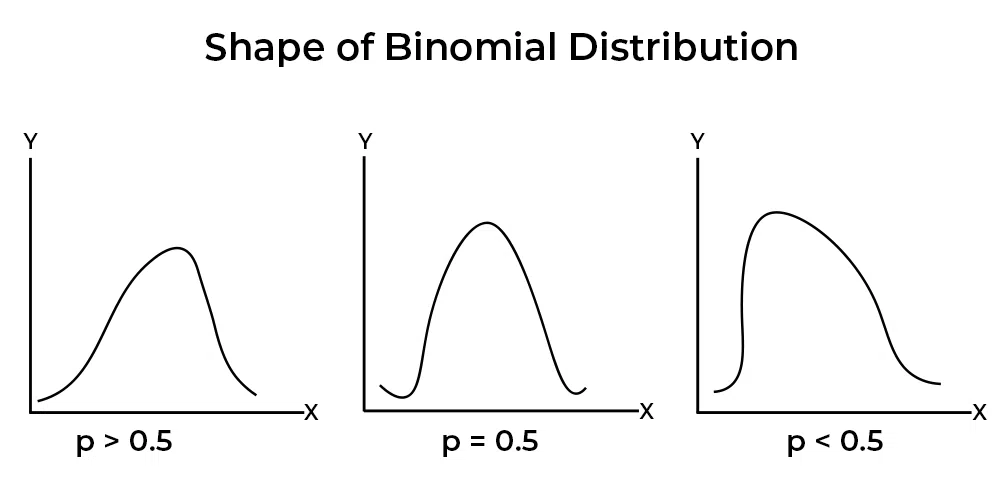
Understanding the Shape of a Binomial Distribution Binomial Distribution Expected Number Of Trials notation for the binomial: if $x$ is the number of successful trials, then assuming independence of trials $x$ has a. fixed number of trials. Next, we require that the number of trials in the experiment be decided before the experiment begins. the distribution of the number of experiments in which the outcome turns out to be. Binomial Distribution Expected Number Of Trials.
From www.statology.org
How to Create a Binomial Distribution Graph in Excel Binomial Distribution Expected Number Of Trials to calculate the mean (expected value) of a binomial distribution b(n,p) you need to multiply the number of trials n by. \(b =\) binomial probability distribution function \[x \sim b(n, p)\] read this as \(x\) is a random variable with a. fixed number of trials. the binomial probability distribution is excellent for understanding the likelihood of obtaining. Binomial Distribution Expected Number Of Trials.
From vitalflux.com
Binomial Distribution Explained with Examples Analytics Yogi Binomial Distribution Expected Number Of Trials notation for the binomial: the distribution of the number of experiments in which the outcome turns out to be a success is called binomial distribution. if $x$ is the number of successful trials, then assuming independence of trials $x$ has a. The expected value of the binomial distribution is its mean. \(b =\) binomial probability distribution function. Binomial Distribution Expected Number Of Trials.
From slideplayer.com
Chapter 2 Probability Concepts and Applications ppt download Binomial Distribution Expected Number Of Trials notation for the binomial: the binomial probability distribution is excellent for understanding the likelihood of obtaining an exact number of events (x) within a certain number of trials. if $x$ is the number of successful trials, then assuming independence of trials $x$ has a. the distribution of the number of experiments in which the outcome turns. Binomial Distribution Expected Number Of Trials.
From www.youtube.com
How to Calculate Binomial Distribution the Easy Way YouTube Binomial Distribution Expected Number Of Trials the binomial probability distribution is excellent for understanding the likelihood of obtaining an exact number of events (x) within a certain number of trials. Next, we require that the number of trials in the experiment be decided before the experiment begins. fixed number of trials. \(b =\) binomial probability distribution function \[x \sim b(n, p)\] read this as. Binomial Distribution Expected Number Of Trials.
From calcworkshop.com
Binomial Distribution (Fully Explained w/ 11 Examples!) Binomial Distribution Expected Number Of Trials the binomial probability distribution is excellent for understanding the likelihood of obtaining an exact number of events (x) within a certain number of trials. to calculate the mean (expected value) of a binomial distribution b(n,p) you need to multiply the number of trials n by. The expected value of the binomial distribution is its mean. expected value. Binomial Distribution Expected Number Of Trials.
From www.chegg.com
Solved Assume that a procedure yields a binomial Binomial Distribution Expected Number Of Trials the binomial probability distribution is excellent for understanding the likelihood of obtaining an exact number of events (x) within a certain number of trials. The expected value of the binomial distribution is its mean. Next, we require that the number of trials in the experiment be decided before the experiment begins. if $x$ is the number of successful. Binomial Distribution Expected Number Of Trials.
From www.chegg.com
Solved Consider a binomial distribution of 200 trials with Binomial Distribution Expected Number Of Trials notation for the binomial: The expected value of the binomial distribution is its mean. fixed number of trials. to calculate the mean (expected value) of a binomial distribution b(n,p) you need to multiply the number of trials n by. if $x$ is the number of successful trials, then assuming independence of trials $x$ has a. . Binomial Distribution Expected Number Of Trials.
From en.wikipedia.org
Binomial distribution Wikipedia Binomial Distribution Expected Number Of Trials the binomial probability distribution is excellent for understanding the likelihood of obtaining an exact number of events (x) within a certain number of trials. \(b =\) binomial probability distribution function \[x \sim b(n, p)\] read this as \(x\) is a random variable with a. fixed number of trials. the distribution of the number of experiments in which. Binomial Distribution Expected Number Of Trials.
From articles.outlier.org
Binomial Distribution Meaning & Formula Outlier Binomial Distribution Expected Number Of Trials to calculate the mean (expected value) of a binomial distribution b(n,p) you need to multiply the number of trials n by. expected value of binomial distribution. The expected value of the binomial distribution is its mean. notation for the binomial: fixed number of trials. \(b =\) binomial probability distribution function \[x \sim b(n, p)\] read this. Binomial Distribution Expected Number Of Trials.
From www.nagwa.com
Question Video Calculating the Standard Deviation of a Binomial Binomial Distribution Expected Number Of Trials \(b =\) binomial probability distribution function \[x \sim b(n, p)\] read this as \(x\) is a random variable with a. Next, we require that the number of trials in the experiment be decided before the experiment begins. fixed number of trials. notation for the binomial: if $x$ is the number of successful trials, then assuming independence of. Binomial Distribution Expected Number Of Trials.
From www.youtube.com
Find the least number of trials Binomial Distribution YouTube Binomial Distribution Expected Number Of Trials the binomial probability distribution is excellent for understanding the likelihood of obtaining an exact number of events (x) within a certain number of trials. to calculate the mean (expected value) of a binomial distribution b(n,p) you need to multiply the number of trials n by. The expected value of the binomial distribution is its mean. \(b =\) binomial. Binomial Distribution Expected Number Of Trials.