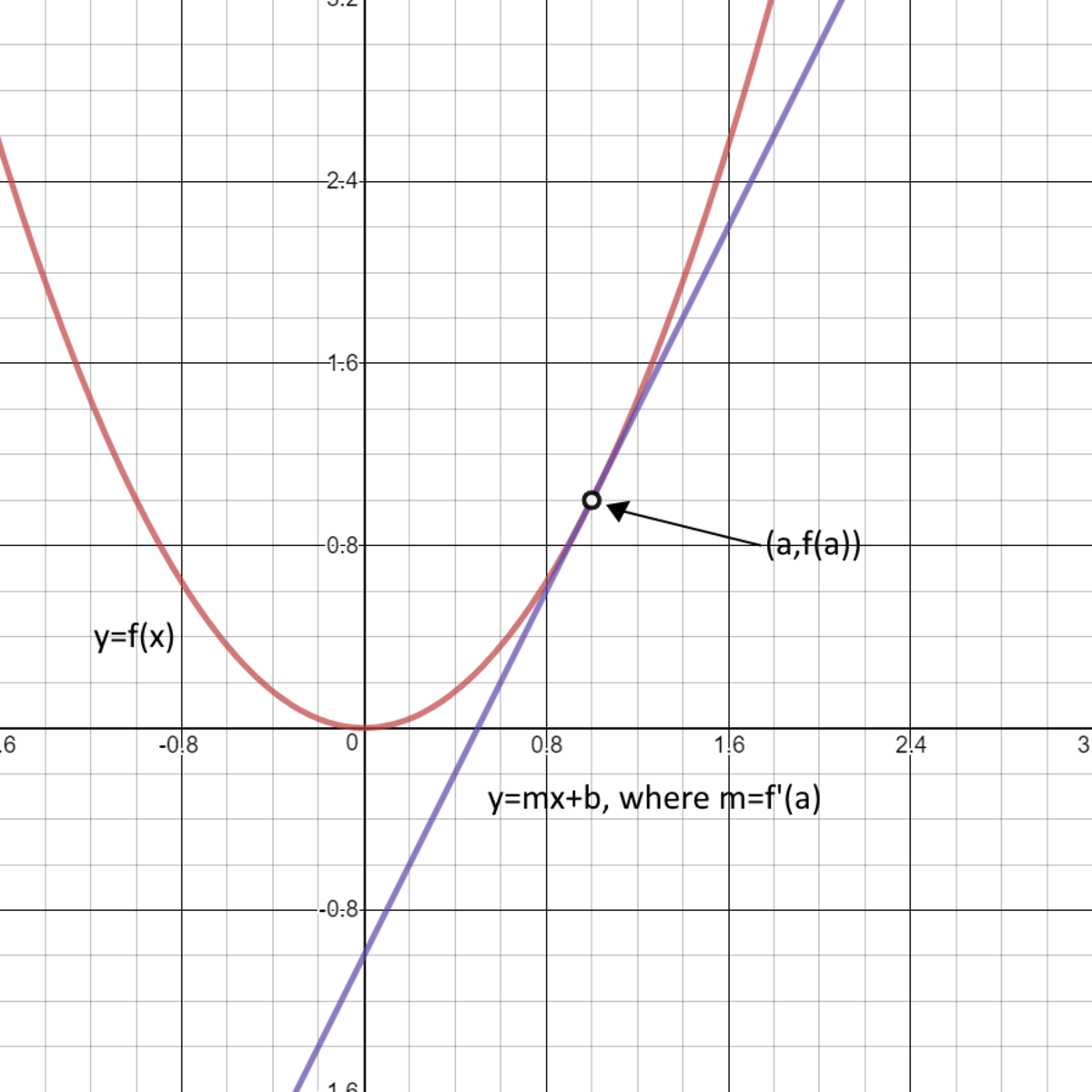
Horizontal And Vertical Tangents Of Parametric Equations . Given \(y=f(x)\), the parametric equations \(x=t\), \(y=f(t)\) produce the same graph. find all points on the curve x = sec θ, y = tan θ x = sec θ, y = tan θ at which horizontal and vertical tangents exist. Suppose that x′(t) and y′(t) are continuous. Then for the curve defined by the parametric equations. the normal line is horizontal (and hence, the tangent line is vertical) when \(\sin t=0\); vertical tangents with parametric curves. it is possible for parametric curves to have horizontal and vertical tangents. this calculus 2 video tutorial explains how to find the points of all horizontal tangent lines and vertical tangent lines of a. converting from rectangular to parametric can be very simple: We will continue the analysis of our parametric curve defined by $x = 6t^3$ and $y = \sin t$. As expected a horizontal tangent occurs whenever d y d x =.
from owlcation.com
it is possible for parametric curves to have horizontal and vertical tangents. Then for the curve defined by the parametric equations. vertical tangents with parametric curves. this calculus 2 video tutorial explains how to find the points of all horizontal tangent lines and vertical tangent lines of a. Given \(y=f(x)\), the parametric equations \(x=t\), \(y=f(t)\) produce the same graph. find all points on the curve x = sec θ, y = tan θ x = sec θ, y = tan θ at which horizontal and vertical tangents exist. Suppose that x′(t) and y′(t) are continuous. As expected a horizontal tangent occurs whenever d y d x =. the normal line is horizontal (and hence, the tangent line is vertical) when \(\sin t=0\); converting from rectangular to parametric can be very simple:
Math How to Find the Tangent Line of a Function in a Point Owlcation
Horizontal And Vertical Tangents Of Parametric Equations find all points on the curve x = sec θ, y = tan θ x = sec θ, y = tan θ at which horizontal and vertical tangents exist. the normal line is horizontal (and hence, the tangent line is vertical) when \(\sin t=0\); it is possible for parametric curves to have horizontal and vertical tangents. We will continue the analysis of our parametric curve defined by $x = 6t^3$ and $y = \sin t$. Given \(y=f(x)\), the parametric equations \(x=t\), \(y=f(t)\) produce the same graph. As expected a horizontal tangent occurs whenever d y d x =. converting from rectangular to parametric can be very simple: vertical tangents with parametric curves. Suppose that x′(t) and y′(t) are continuous. this calculus 2 video tutorial explains how to find the points of all horizontal tangent lines and vertical tangent lines of a. Then for the curve defined by the parametric equations. find all points on the curve x = sec θ, y = tan θ x = sec θ, y = tan θ at which horizontal and vertical tangents exist.
From www.numerade.com
SOLVED Find the unit tangent vector T(t) and find a set of parametric equations for the line Horizontal And Vertical Tangents Of Parametric Equations it is possible for parametric curves to have horizontal and vertical tangents. the normal line is horizontal (and hence, the tangent line is vertical) when \(\sin t=0\); Given \(y=f(x)\), the parametric equations \(x=t\), \(y=f(t)\) produce the same graph. Suppose that x′(t) and y′(t) are continuous. vertical tangents with parametric curves. Then for the curve defined by the. Horizontal And Vertical Tangents Of Parametric Equations.
From owlcation.com
Math How to Find the Tangent Line of a Function in a Point Owlcation Horizontal And Vertical Tangents Of Parametric Equations find all points on the curve x = sec θ, y = tan θ x = sec θ, y = tan θ at which horizontal and vertical tangents exist. Suppose that x′(t) and y′(t) are continuous. Then for the curve defined by the parametric equations. As expected a horizontal tangent occurs whenever d y d x =. the. Horizontal And Vertical Tangents Of Parametric Equations.
From www.youtube.com
Parametric equations of the tangent line (vectors) (KristaKingMath) YouTube Horizontal And Vertical Tangents Of Parametric Equations it is possible for parametric curves to have horizontal and vertical tangents. Then for the curve defined by the parametric equations. find all points on the curve x = sec θ, y = tan θ x = sec θ, y = tan θ at which horizontal and vertical tangents exist. converting from rectangular to parametric can be. Horizontal And Vertical Tangents Of Parametric Equations.
From calcworkshop.com
Parametric Lesson Horizontal And Vertical Tangents Of Parametric Equations the normal line is horizontal (and hence, the tangent line is vertical) when \(\sin t=0\); Suppose that x′(t) and y′(t) are continuous. Given \(y=f(x)\), the parametric equations \(x=t\), \(y=f(t)\) produce the same graph. As expected a horizontal tangent occurs whenever d y d x =. Then for the curve defined by the parametric equations. We will continue the analysis. Horizontal And Vertical Tangents Of Parametric Equations.
From www.youtube.com
Find the Points at which there are Vertical and Horizontal Tangent Lines given Parametric Horizontal And Vertical Tangents Of Parametric Equations it is possible for parametric curves to have horizontal and vertical tangents. Then for the curve defined by the parametric equations. We will continue the analysis of our parametric curve defined by $x = 6t^3$ and $y = \sin t$. As expected a horizontal tangent occurs whenever d y d x =. this calculus 2 video tutorial explains. Horizontal And Vertical Tangents Of Parametric Equations.
From www.youtube.com
Tangent Lines given Parametric Equations YouTube Horizontal And Vertical Tangents Of Parametric Equations the normal line is horizontal (and hence, the tangent line is vertical) when \(\sin t=0\); vertical tangents with parametric curves. it is possible for parametric curves to have horizontal and vertical tangents. We will continue the analysis of our parametric curve defined by $x = 6t^3$ and $y = \sin t$. converting from rectangular to parametric. Horizontal And Vertical Tangents Of Parametric Equations.
From www.youtube.com
Tangent Lines of Parametric Curves YouTube Horizontal And Vertical Tangents Of Parametric Equations We will continue the analysis of our parametric curve defined by $x = 6t^3$ and $y = \sin t$. the normal line is horizontal (and hence, the tangent line is vertical) when \(\sin t=0\); it is possible for parametric curves to have horizontal and vertical tangents. Then for the curve defined by the parametric equations. vertical tangents. Horizontal And Vertical Tangents Of Parametric Equations.
From www.numerade.com
SOLVED 2) Find a set of parametric equations for the tangent line to the curve of intersection Horizontal And Vertical Tangents Of Parametric Equations this calculus 2 video tutorial explains how to find the points of all horizontal tangent lines and vertical tangent lines of a. vertical tangents with parametric curves. Then for the curve defined by the parametric equations. As expected a horizontal tangent occurs whenever d y d x =. Given \(y=f(x)\), the parametric equations \(x=t\), \(y=f(t)\) produce the same. Horizontal And Vertical Tangents Of Parametric Equations.
From calcworkshop.com
Parametric Lesson Horizontal And Vertical Tangents Of Parametric Equations Suppose that x′(t) and y′(t) are continuous. it is possible for parametric curves to have horizontal and vertical tangents. We will continue the analysis of our parametric curve defined by $x = 6t^3$ and $y = \sin t$. Then for the curve defined by the parametric equations. find all points on the curve x = sec θ, y. Horizontal And Vertical Tangents Of Parametric Equations.
From www.youtube.com
Find points on curve where tangent is horizontal, vertical for x = t^3 3t, y= t^2 3 Horizontal And Vertical Tangents Of Parametric Equations Then for the curve defined by the parametric equations. converting from rectangular to parametric can be very simple: As expected a horizontal tangent occurs whenever d y d x =. Suppose that x′(t) and y′(t) are continuous. find all points on the curve x = sec θ, y = tan θ x = sec θ, y = tan. Horizontal And Vertical Tangents Of Parametric Equations.
From www.numerade.com
SOLVED Sketch the parametric curve x =t2 t,y =t 3t and determine the location (x, y and t Horizontal And Vertical Tangents Of Parametric Equations Given \(y=f(x)\), the parametric equations \(x=t\), \(y=f(t)\) produce the same graph. this calculus 2 video tutorial explains how to find the points of all horizontal tangent lines and vertical tangent lines of a. converting from rectangular to parametric can be very simple: the normal line is horizontal (and hence, the tangent line is vertical) when \(\sin t=0\);. Horizontal And Vertical Tangents Of Parametric Equations.
From www.wikihow.com
How to Find the Equation of a Tangent Line 8 Steps Horizontal And Vertical Tangents Of Parametric Equations Suppose that x′(t) and y′(t) are continuous. Given \(y=f(x)\), the parametric equations \(x=t\), \(y=f(t)\) produce the same graph. it is possible for parametric curves to have horizontal and vertical tangents. We will continue the analysis of our parametric curve defined by $x = 6t^3$ and $y = \sin t$. Then for the curve defined by the parametric equations. . Horizontal And Vertical Tangents Of Parametric Equations.
From www.youtube.com
Horizontal and Vertical Tangent Lines to Polar Curves YouTube Horizontal And Vertical Tangents Of Parametric Equations Given \(y=f(x)\), the parametric equations \(x=t\), \(y=f(t)\) produce the same graph. converting from rectangular to parametric can be very simple: this calculus 2 video tutorial explains how to find the points of all horizontal tangent lines and vertical tangent lines of a. As expected a horizontal tangent occurs whenever d y d x =. vertical tangents with. Horizontal And Vertical Tangents Of Parametric Equations.
From www.youtube.com
Determine the Points Where the Tangent Lines are Horizontal or Vertical Using Parametric Horizontal And Vertical Tangents Of Parametric Equations it is possible for parametric curves to have horizontal and vertical tangents. Then for the curve defined by the parametric equations. Suppose that x′(t) and y′(t) are continuous. Given \(y=f(x)\), the parametric equations \(x=t\), \(y=f(t)\) produce the same graph. vertical tangents with parametric curves. find all points on the curve x = sec θ, y = tan. Horizontal And Vertical Tangents Of Parametric Equations.
From www.youtube.com
Horizontal Tangent Lines & Vertical Tangent Lines In Polar Form YouTube Horizontal And Vertical Tangents Of Parametric Equations vertical tangents with parametric curves. We will continue the analysis of our parametric curve defined by $x = 6t^3$ and $y = \sin t$. the normal line is horizontal (and hence, the tangent line is vertical) when \(\sin t=0\); it is possible for parametric curves to have horizontal and vertical tangents. this calculus 2 video tutorial. Horizontal And Vertical Tangents Of Parametric Equations.
From www.slideserve.com
PPT Tangent Lines and Arc Length Parametric Equations PowerPoint Presentation ID3734094 Horizontal And Vertical Tangents Of Parametric Equations vertical tangents with parametric curves. it is possible for parametric curves to have horizontal and vertical tangents. As expected a horizontal tangent occurs whenever d y d x =. Then for the curve defined by the parametric equations. the normal line is horizontal (and hence, the tangent line is vertical) when \(\sin t=0\); We will continue the. Horizontal And Vertical Tangents Of Parametric Equations.
From www.tessshebaylo.com
Equation Of Tangent Line Parametric Calculator Tessshebaylo Horizontal And Vertical Tangents Of Parametric Equations As expected a horizontal tangent occurs whenever d y d x =. vertical tangents with parametric curves. converting from rectangular to parametric can be very simple: it is possible for parametric curves to have horizontal and vertical tangents. Given \(y=f(x)\), the parametric equations \(x=t\), \(y=f(t)\) produce the same graph. the normal line is horizontal (and hence,. Horizontal And Vertical Tangents Of Parametric Equations.
From www.cuemath.com
Tangent Definition Equation and Calculator Cuemath Horizontal And Vertical Tangents Of Parametric Equations find all points on the curve x = sec θ, y = tan θ x = sec θ, y = tan θ at which horizontal and vertical tangents exist. We will continue the analysis of our parametric curve defined by $x = 6t^3$ and $y = \sin t$. Suppose that x′(t) and y′(t) are continuous. As expected a horizontal. Horizontal And Vertical Tangents Of Parametric Equations.
From www.youtube.com
Horizontal Tangent Lines and Vertical Tangent Lines of Parametric Functions Calculus 2 YouTube Horizontal And Vertical Tangents Of Parametric Equations Then for the curve defined by the parametric equations. it is possible for parametric curves to have horizontal and vertical tangents. We will continue the analysis of our parametric curve defined by $x = 6t^3$ and $y = \sin t$. Given \(y=f(x)\), the parametric equations \(x=t\), \(y=f(t)\) produce the same graph. vertical tangents with parametric curves. find. Horizontal And Vertical Tangents Of Parametric Equations.
From www.slideserve.com
PPT The Calculus of Parametric Equations PowerPoint Presentation, free download ID4494962 Horizontal And Vertical Tangents Of Parametric Equations vertical tangents with parametric curves. find all points on the curve x = sec θ, y = tan θ x = sec θ, y = tan θ at which horizontal and vertical tangents exist. We will continue the analysis of our parametric curve defined by $x = 6t^3$ and $y = \sin t$. converting from rectangular to. Horizontal And Vertical Tangents Of Parametric Equations.
From www.slideserve.com
PPT Parametric Equations PowerPoint Presentation, free download ID1340261 Horizontal And Vertical Tangents Of Parametric Equations vertical tangents with parametric curves. find all points on the curve x = sec θ, y = tan θ x = sec θ, y = tan θ at which horizontal and vertical tangents exist. Given \(y=f(x)\), the parametric equations \(x=t\), \(y=f(t)\) produce the same graph. We will continue the analysis of our parametric curve defined by $x =. Horizontal And Vertical Tangents Of Parametric Equations.
From www.numerade.com
A curve C is defined by the parametric equations x=t^2 y=t^33 t (a) Show that C has two Horizontal And Vertical Tangents Of Parametric Equations Given \(y=f(x)\), the parametric equations \(x=t\), \(y=f(t)\) produce the same graph. vertical tangents with parametric curves. As expected a horizontal tangent occurs whenever d y d x =. it is possible for parametric curves to have horizontal and vertical tangents. Then for the curve defined by the parametric equations. converting from rectangular to parametric can be very. Horizontal And Vertical Tangents Of Parametric Equations.
From www.youtube.com
Math 151 Tangent Lines, Vertical, and Horizontal for Parametric Equations YouTube Horizontal And Vertical Tangents Of Parametric Equations the normal line is horizontal (and hence, the tangent line is vertical) when \(\sin t=0\); vertical tangents with parametric curves. As expected a horizontal tangent occurs whenever d y d x =. Given \(y=f(x)\), the parametric equations \(x=t\), \(y=f(t)\) produce the same graph. We will continue the analysis of our parametric curve defined by $x = 6t^3$ and. Horizontal And Vertical Tangents Of Parametric Equations.
From www.youtube.com
Finding points with vertical tangents YouTube Horizontal And Vertical Tangents Of Parametric Equations We will continue the analysis of our parametric curve defined by $x = 6t^3$ and $y = \sin t$. Given \(y=f(x)\), the parametric equations \(x=t\), \(y=f(t)\) produce the same graph. converting from rectangular to parametric can be very simple: Suppose that x′(t) and y′(t) are continuous. find all points on the curve x = sec θ, y =. Horizontal And Vertical Tangents Of Parametric Equations.
From socratic.org
How do you find the horizontal and vertical tangents to x = Cos(3t) and y = 2sin(t)? Socratic Horizontal And Vertical Tangents Of Parametric Equations this calculus 2 video tutorial explains how to find the points of all horizontal tangent lines and vertical tangent lines of a. As expected a horizontal tangent occurs whenever d y d x =. vertical tangents with parametric curves. find all points on the curve x = sec θ, y = tan θ x = sec θ,. Horizontal And Vertical Tangents Of Parametric Equations.
From www.numerade.com
SOLVED2) Identify the vertical, and horizontal tangents to the parametric curve x = 2t3 3t2 36t Horizontal And Vertical Tangents Of Parametric Equations Suppose that x′(t) and y′(t) are continuous. it is possible for parametric curves to have horizontal and vertical tangents. As expected a horizontal tangent occurs whenever d y d x =. converting from rectangular to parametric can be very simple: the normal line is horizontal (and hence, the tangent line is vertical) when \(\sin t=0\); Then for. Horizontal And Vertical Tangents Of Parametric Equations.
From www.youtube.com
Ex Find Parametric Equations For Ellipse Using Sine And Cosine From a Graph YouTube Horizontal And Vertical Tangents Of Parametric Equations it is possible for parametric curves to have horizontal and vertical tangents. We will continue the analysis of our parametric curve defined by $x = 6t^3$ and $y = \sin t$. vertical tangents with parametric curves. this calculus 2 video tutorial explains how to find the points of all horizontal tangent lines and vertical tangent lines of. Horizontal And Vertical Tangents Of Parametric Equations.
From www.youtube.com
Parametric Equations Horizontal and Vertical Tangents YouTube Horizontal And Vertical Tangents Of Parametric Equations the normal line is horizontal (and hence, the tangent line is vertical) when \(\sin t=0\); it is possible for parametric curves to have horizontal and vertical tangents. As expected a horizontal tangent occurs whenever d y d x =. Then for the curve defined by the parametric equations. vertical tangents with parametric curves. this calculus 2. Horizontal And Vertical Tangents Of Parametric Equations.
From www.showme.com
4.2 Horizontal tangent line Math ShowMe Horizontal And Vertical Tangents Of Parametric Equations vertical tangents with parametric curves. this calculus 2 video tutorial explains how to find the points of all horizontal tangent lines and vertical tangent lines of a. Given \(y=f(x)\), the parametric equations \(x=t\), \(y=f(t)\) produce the same graph. As expected a horizontal tangent occurs whenever d y d x =. it is possible for parametric curves to. Horizontal And Vertical Tangents Of Parametric Equations.
From www.slideserve.com
PPT Parametric Derivatives PowerPoint Presentation, free download ID2536119 Horizontal And Vertical Tangents Of Parametric Equations it is possible for parametric curves to have horizontal and vertical tangents. Then for the curve defined by the parametric equations. We will continue the analysis of our parametric curve defined by $x = 6t^3$ and $y = \sin t$. As expected a horizontal tangent occurs whenever d y d x =. the normal line is horizontal (and. Horizontal And Vertical Tangents Of Parametric Equations.
From www.numerade.com
SOLVED Consider the parametric curve x = (t2 2t + 1e3t , y = (t2 + 4t + 4)e3t Find points (x,y Horizontal And Vertical Tangents Of Parametric Equations Given \(y=f(x)\), the parametric equations \(x=t\), \(y=f(t)\) produce the same graph. converting from rectangular to parametric can be very simple: Suppose that x′(t) and y′(t) are continuous. vertical tangents with parametric curves. As expected a horizontal tangent occurs whenever d y d x =. We will continue the analysis of our parametric curve defined by $x = 6t^3$. Horizontal And Vertical Tangents Of Parametric Equations.
From www.youtube.com
Video 2069.2 Tangent line on an Astroid, Parametric Equations YouTube Horizontal And Vertical Tangents Of Parametric Equations We will continue the analysis of our parametric curve defined by $x = 6t^3$ and $y = \sin t$. find all points on the curve x = sec θ, y = tan θ x = sec θ, y = tan θ at which horizontal and vertical tangents exist. Then for the curve defined by the parametric equations. vertical. Horizontal And Vertical Tangents Of Parametric Equations.
From www.youtube.com
Find equation of the tangent at t = pi for x = t cos t, and y = t sin t. Parametric equations Horizontal And Vertical Tangents Of Parametric Equations As expected a horizontal tangent occurs whenever d y d x =. Given \(y=f(x)\), the parametric equations \(x=t\), \(y=f(t)\) produce the same graph. Then for the curve defined by the parametric equations. it is possible for parametric curves to have horizontal and vertical tangents. We will continue the analysis of our parametric curve defined by $x = 6t^3$ and. Horizontal And Vertical Tangents Of Parametric Equations.
From www.youtube.com
Ex 1 Equation of a Tangent Line to a Curve Given by Parametric Equations YouTube Horizontal And Vertical Tangents Of Parametric Equations this calculus 2 video tutorial explains how to find the points of all horizontal tangent lines and vertical tangent lines of a. find all points on the curve x = sec θ, y = tan θ x = sec θ, y = tan θ at which horizontal and vertical tangents exist. vertical tangents with parametric curves. . Horizontal And Vertical Tangents Of Parametric Equations.
From www.youtube.com
How to Find an Equation of a Tangent Line where the Curve Crosses ItselfParametric Form YouTube Horizontal And Vertical Tangents Of Parametric Equations vertical tangents with parametric curves. Given \(y=f(x)\), the parametric equations \(x=t\), \(y=f(t)\) produce the same graph. it is possible for parametric curves to have horizontal and vertical tangents. Then for the curve defined by the parametric equations. We will continue the analysis of our parametric curve defined by $x = 6t^3$ and $y = \sin t$. find. Horizontal And Vertical Tangents Of Parametric Equations.