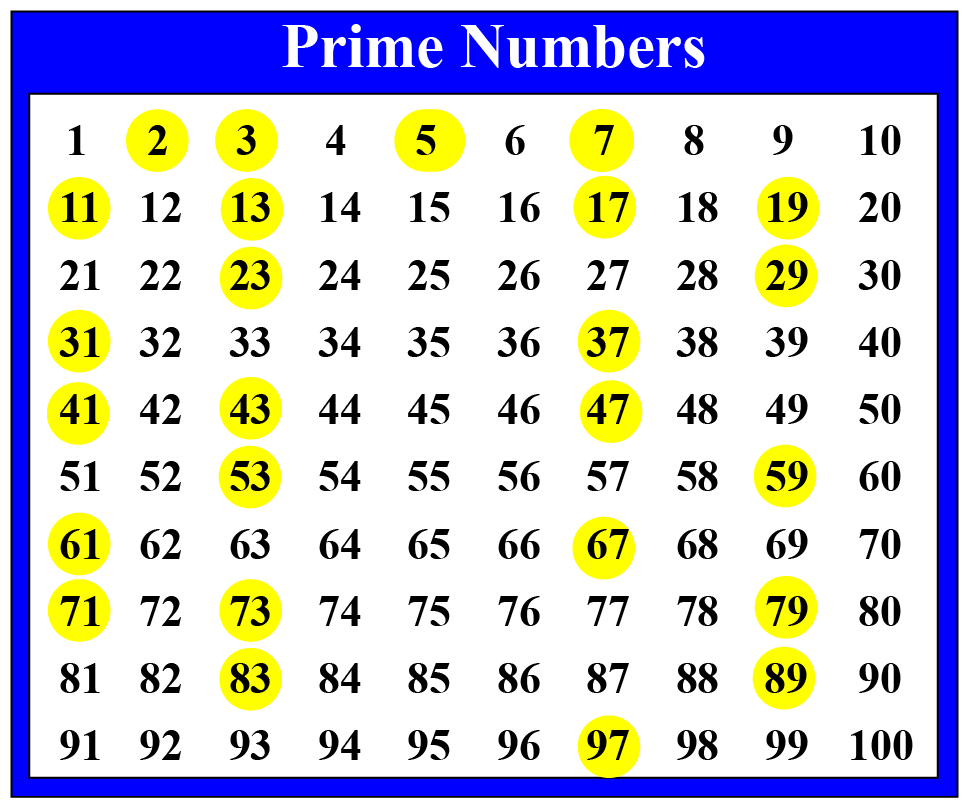
Is The Set Of All Prime Numbers Countable at Krystal Terry blog

Is The Set Of All Prime Numbers Countable. For example, the primes are countable because we can pair 1 with the first. Sets equivalent to the positive integers are said to be countable. Integers, rational numbers and many. The proof of (i) is the same as the proof that \(t\) is uncountable in the proof of theorem 1.20. Use theorem 9.15 and theorem 9.17. Since a a is infinite (due to euclid),. Is the set of all prime numbers countable or uncountable? Given that the prime numbers are a subset of the natural numbers and (by definition) the latter are countably infinite, the primes. If a ⊆n a ⊆ n then a a is either finite, empty or countable. We could simply use a theorem that states: If it is countable, show a 1 to 1 correspondence between the prime. Prove that if \(a\) is countably infinite and. The proof of (ii) consists of writing. The set \(\mathbb{q}\) of all rational numbers is countable.

Use theorem 9.15 and theorem 9.17. The proof of (ii) consists of writing. Sets equivalent to the positive integers are said to be countable. If a ⊆n a ⊆ n then a a is either finite, empty or countable. If it is countable, show a 1 to 1 correspondence between the prime. Given that the prime numbers are a subset of the natural numbers and (by definition) the latter are countably infinite, the primes. The proof of (i) is the same as the proof that \(t\) is uncountable in the proof of theorem 1.20. The set \(\mathbb{q}\) of all rational numbers is countable. We could simply use a theorem that states: For example, the primes are countable because we can pair 1 with the first.

Is 101 a Prime Number ? Cuemath

Is The Set Of All Prime Numbers Countable If it is countable, show a 1 to 1 correspondence between the prime. Prove that if \(a\) is countably infinite and. Since a a is infinite (due to euclid),. Use theorem 9.15 and theorem 9.17. We could simply use a theorem that states: Given that the prime numbers are a subset of the natural numbers and (by definition) the latter are countably infinite, the primes. The set \(\mathbb{q}\) of all rational numbers is countable. For example, the primes are countable because we can pair 1 with the first. Sets equivalent to the positive integers are said to be countable. Is the set of all prime numbers countable or uncountable? Integers, rational numbers and many. The proof of (i) is the same as the proof that \(t\) is uncountable in the proof of theorem 1.20. If a ⊆n a ⊆ n then a a is either finite, empty or countable. The proof of (ii) consists of writing. If it is countable, show a 1 to 1 correspondence between the prime.