Orthogonal Matrix Def . A matrix a ∈ gl. A t a = a a t = i. When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. Orthogonal matrices are those preserving the dot product. A square matrix a is orthogonal if its transpose a t is also its inverse a − 1. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. An orthogonal matrix is a square matrix in which the rows and columns are mutually orthogonal unit vectors and the transpose of an orthogonal matrix is its. The precise definition is as follows. N (r) is orthogonal if av · aw = v · w for all vectors v. Learn more about the orthogonal. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. Also, the product of an orthogonal matrix and its transpose is equal to i.
from www.chegg.com
Also, the product of an orthogonal matrix and its transpose is equal to i. An orthogonal matrix is a square matrix in which the rows and columns are mutually orthogonal unit vectors and the transpose of an orthogonal matrix is its. Orthogonal matrices are those preserving the dot product. A square matrix a is orthogonal if its transpose a t is also its inverse a − 1. The precise definition is as follows. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. A matrix a ∈ gl. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. N (r) is orthogonal if av · aw = v · w for all vectors v.
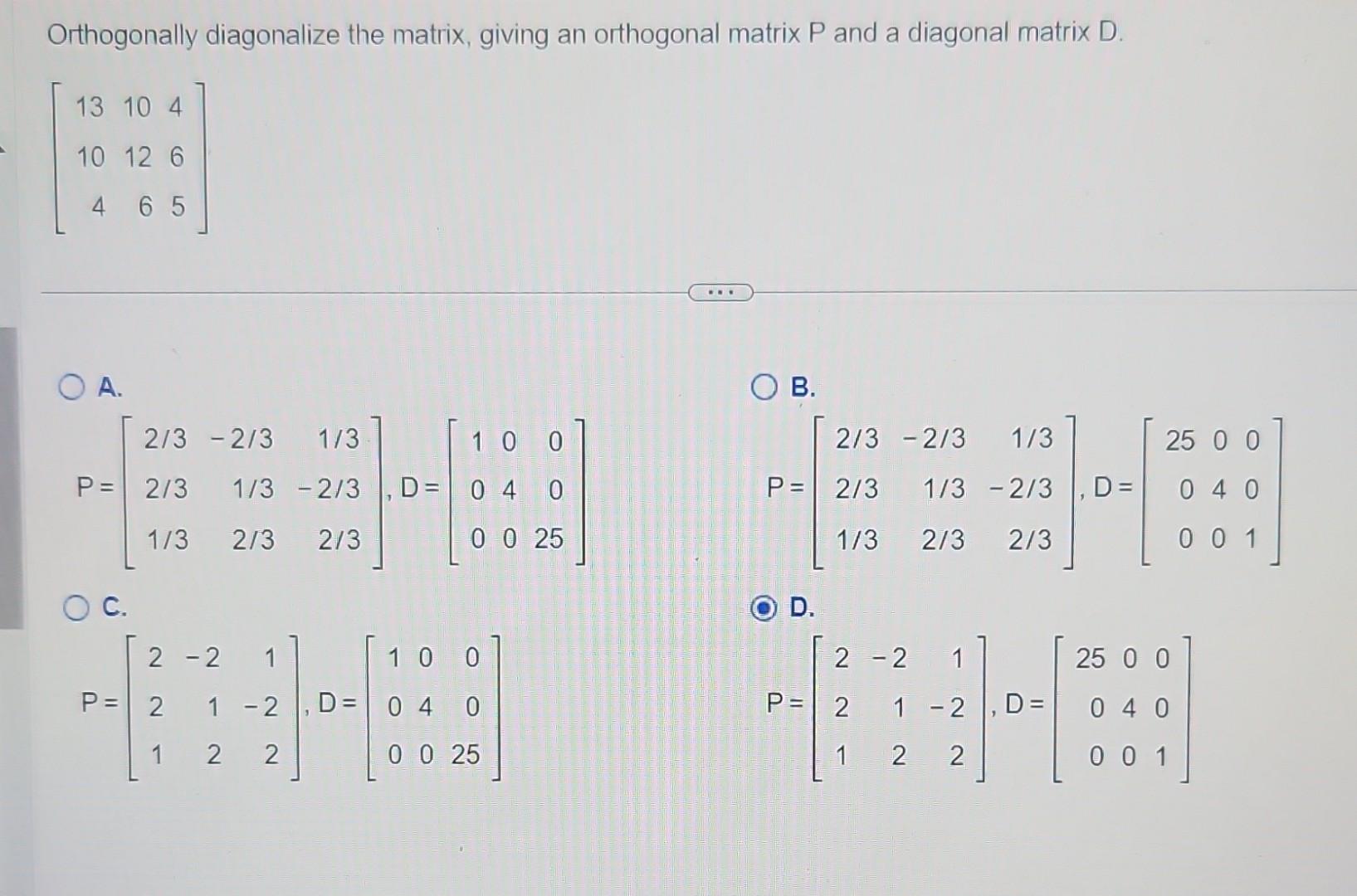
Solved Orthogonally diagonalize the matrix, giving an
Orthogonal Matrix Def Learn more about the orthogonal. A t a = a a t = i. An orthogonal matrix is a square matrix in which the rows and columns are mutually orthogonal unit vectors and the transpose of an orthogonal matrix is its. N (r) is orthogonal if av · aw = v · w for all vectors v. Orthogonal matrices are those preserving the dot product. When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. Learn more about the orthogonal. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. The precise definition is as follows. Also, the product of an orthogonal matrix and its transpose is equal to i. A square matrix a is orthogonal if its transpose a t is also its inverse a − 1. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. A matrix a ∈ gl.
From www.youtube.com
Orthogonal Matrix example YouTube Orthogonal Matrix Def When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. Orthogonal matrices are those preserving the dot product. A t a = a a t = i. N (r) is orthogonal. Orthogonal Matrix Def.
From www.studypool.com
SOLUTION Symmetric skew symmetric and orthogonal matrices Studypool Orthogonal Matrix Def A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. A square matrix a is orthogonal if its transpose a t is also its inverse a − 1. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. A matrix. Orthogonal Matrix Def.
From www.slideserve.com
PPT 6.4 Best Approximation; Least Squares PowerPoint Presentation Orthogonal Matrix Def A square matrix a is orthogonal if its transpose a t is also its inverse a − 1. A t a = a a t = i. An orthogonal matrix is a square matrix in which the rows and columns are mutually orthogonal unit vectors and the transpose of an orthogonal matrix is its. N (r) is orthogonal if av. Orthogonal Matrix Def.
From www.chegg.com
Solved Orthogonally diagonalize the matrix, giving an Orthogonal Matrix Def Also, the product of an orthogonal matrix and its transpose is equal to i. Learn more about the orthogonal. An orthogonal matrix is a square matrix in which the rows and columns are mutually orthogonal unit vectors and the transpose of an orthogonal matrix is its. A square matrix a is orthogonal if its transpose a t is also its. Orthogonal Matrix Def.
From claimyourpowerblog.wordpress.com
Daily Notes 08.15.18 ClaimYourPowerBlog Orthogonal Matrix Def A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. A matrix 'a' is orthogonal if and only if its inverse is equal. Orthogonal Matrix Def.
From www.chegg.com
Solved Definition 3.2.7 Special Orthogonal Group The Orthogonal Matrix Def Learn more about the orthogonal. A square matrix a is orthogonal if its transpose a t is also its inverse a − 1. N (r) is orthogonal if av · aw = v · w for all vectors v. A t a = a a t = i. An orthogonal matrix is a square matrix in which the rows and. Orthogonal Matrix Def.
From www.chegg.com
Solved Find orthogonal matrix of following matrix. (hint if Orthogonal Matrix Def When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. An orthogonal matrix is a square matrix in which the rows and columns. Orthogonal Matrix Def.
From www.youtube.com
Properties of Orthogonal Matrix Example1 YouTube Orthogonal Matrix Def N (r) is orthogonal if av · aw = v · w for all vectors v. Learn more about the orthogonal. Also, the product of an orthogonal matrix and its transpose is equal to i. A square matrix a is orthogonal if its transpose a t is also its inverse a − 1. A matrix 'a' is orthogonal if and. Orthogonal Matrix Def.
From www.machinelearningplus.com
Linear Algebra Archives Machine Learning Plus Orthogonal Matrix Def A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called. Orthogonal Matrix Def.
From www.toppr.com
An orthogonal matrix is Maths Questions Orthogonal Matrix Def An orthogonal matrix is a square matrix in which the rows and columns are mutually orthogonal unit vectors and the transpose of an orthogonal matrix is its. Also, the product of an orthogonal matrix and its transpose is equal to i. A matrix a ∈ gl. A matrix 'a' is orthogonal if and only if its inverse is equal to. Orthogonal Matrix Def.
From teamlab.github.io
Basic Linear Algebra Orthogonal Matrix Def N (r) is orthogonal if av · aw = v · w for all vectors v. Also, the product of an orthogonal matrix and its transpose is equal to i. Learn more about the orthogonal. When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. A n×n. Orthogonal Matrix Def.
From www.slideserve.com
PPT ENGG2013 Unit 19 The principal axes theorem PowerPoint Orthogonal Matrix Def A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. N (r) is orthogonal if av · aw = v · w for all vectors v. Also, the product of. Orthogonal Matrix Def.
From ar.inspiredpencil.com
Orthogonal Matrix Orthogonal Matrix Def A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. Orthogonal matrices are those preserving the dot product. A matrix a ∈ gl. A t a = a a t = i. N (r) is orthogonal if av · aw = v · w for all. Orthogonal Matrix Def.
From slidetodoc.com
Orthogonal Vector Hungyi Lee Orthogonal Set A set Orthogonal Matrix Def N (r) is orthogonal if av · aw = v · w for all vectors v. A t a = a a t = i. An orthogonal matrix is a square matrix in which the rows and columns are mutually orthogonal unit vectors and the transpose of an orthogonal matrix is its. Learn more about the orthogonal. A matrix 'a'. Orthogonal Matrix Def.
From datascienceparichay.com
Numpy Check If a Matrix is Orthogonal Data Science Parichay Orthogonal Matrix Def Also, the product of an orthogonal matrix and its transpose is equal to i. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. Learn more about the orthogonal. The precise definition is as follows. A matrix a ∈ gl. When an \(n \times n\) matrix. Orthogonal Matrix Def.
From www.youtube.com
How to prove ORTHOGONAL Matrices YouTube Orthogonal Matrix Def When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. A square matrix a is orthogonal if its transpose a t is also its inverse a − 1. A matrix a ∈ gl. A t a = a a t = i. Orthogonal matrices are those preserving. Orthogonal Matrix Def.
From rilohs.weebly.com
Orthogonal matrix rilohs Orthogonal Matrix Def When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. The precise definition is as follows. A matrix a ∈ gl. A t a = a a t = i. Orthogonal matrices are those preserving the dot product. An orthogonal matrix is a square matrix in which. Orthogonal Matrix Def.
From www.slideserve.com
PPT Agenda for understand req activity PowerPoint Presentation, free Orthogonal Matrix Def N (r) is orthogonal if av · aw = v · w for all vectors v. Also, the product of an orthogonal matrix and its transpose is equal to i. A t a = a a t = i. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is. Orthogonal Matrix Def.
From www.youtube.com
【Orthogonality】06 Orthogonal matrix YouTube Orthogonal Matrix Def A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. Also, the product of an orthogonal matrix and its transpose is equal to i. A square matrix a is orthogonal. Orthogonal Matrix Def.
From www.chegg.com
Solved Problem 12 Practice with Orthogonal Matrices Consider Orthogonal Matrix Def A square matrix a is orthogonal if its transpose a t is also its inverse a − 1. An orthogonal matrix is a square matrix in which the rows and columns are mutually orthogonal unit vectors and the transpose of an orthogonal matrix is its. N (r) is orthogonal if av · aw = v · w for all vectors. Orthogonal Matrix Def.
From slidetodoc.com
Orthogonal Vector Hungyi Lee Orthogonal Set A set Orthogonal Matrix Def A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. Also, the product of an orthogonal matrix and its transpose is equal to i. The precise definition is as follows. Learn more about the orthogonal. A t a = a a t = i. Orthogonal matrices. Orthogonal Matrix Def.
From scoop.eduncle.com
Find orthogonal matrix and unitary matrix Orthogonal Matrix Def A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. The precise definition is as follows. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. A matrix a ∈ gl. Orthogonal matrices are those preserving the dot product. Also,. Orthogonal Matrix Def.
From inputone.weebly.com
inputone Blog Orthogonal Matrix Def When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. A square matrix a is orthogonal if its transpose a t is also its inverse a − 1. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and. Orthogonal Matrix Def.
From inputone.weebly.com
inputone Blog Orthogonal Matrix Def Also, the product of an orthogonal matrix and its transpose is equal to i. When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. A square matrix a is orthogonal if. Orthogonal Matrix Def.
From askfilo.com
Example 8. If A is an invertible matrix and orthogonal matrix of the orde.. Orthogonal Matrix Def N (r) is orthogonal if av · aw = v · w for all vectors v. Orthogonal matrices are those preserving the dot product. The precise definition is as follows. An orthogonal matrix is a square matrix in which the rows and columns are mutually orthogonal unit vectors and the transpose of an orthogonal matrix is its. A matrix 'a'. Orthogonal Matrix Def.
From limfadreams.weebly.com
Orthogonal matrix limfadreams Orthogonal Matrix Def A matrix a ∈ gl. Learn more about the orthogonal. The precise definition is as follows. When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is. Orthogonal Matrix Def.
From www.youtube.com
Orthogonal Matrix What is orthogonal Matrix Important Questions on Orthogonal Matrix Def An orthogonal matrix is a square matrix in which the rows and columns are mutually orthogonal unit vectors and the transpose of an orthogonal matrix is its. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. The precise definition is as follows. When an \(n. Orthogonal Matrix Def.
From www.chegg.com
Solved a. Which of the matrices are orthogonal (has Orthogonal Matrix Def Also, the product of an orthogonal matrix and its transpose is equal to i. The precise definition is as follows. A matrix a ∈ gl. An orthogonal matrix is a square matrix in which the rows and columns are mutually orthogonal unit vectors and the transpose of an orthogonal matrix is its. A square matrix a is orthogonal if its. Orthogonal Matrix Def.
From www.youtube.com
Orthogonal Matrix Definition Example Properties Class 12 Maths YouTube Orthogonal Matrix Def When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. Orthogonal matrices are those preserving the dot product. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. The precise definition is as follows. Also, the product of an orthogonal matrix. Orthogonal Matrix Def.
From youtube.com
1.3 Orthogonal Vectors YouTube Orthogonal Matrix Def An orthogonal matrix is a square matrix in which the rows and columns are mutually orthogonal unit vectors and the transpose of an orthogonal matrix is its. A matrix a ∈ gl. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. Also, the product of. Orthogonal Matrix Def.
From www.kashishkumar.com
Linear Algebra for Machine Learning using Python Orthogonal Matrix Def The precise definition is as follows. A square matrix a is orthogonal if its transpose a t is also its inverse a − 1. Orthogonal matrices are those preserving the dot product. Learn more about the orthogonal. A matrix a ∈ gl. When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix. Orthogonal Matrix Def.
From medium.com
[Linear Algebra] 9. Properties of orthogonal matrices by Jun jun Orthogonal Matrix Def A t a = a a t = i. A square matrix a is orthogonal if its transpose a t is also its inverse a − 1. N (r) is orthogonal if av · aw = v · w for all vectors v. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of. Orthogonal Matrix Def.
From inputone.weebly.com
inputone Blog Orthogonal Matrix Def N (r) is orthogonal if av · aw = v · w for all vectors v. The precise definition is as follows. Also, the product of an orthogonal matrix and its transpose is equal to i. A matrix a ∈ gl. Learn more about the orthogonal. A matrix 'a' is orthogonal if and only if its inverse is equal to. Orthogonal Matrix Def.
From www.youtube.com
How to Prove that a Matrix is Orthogonal YouTube Orthogonal Matrix Def A matrix a ∈ gl. A square matrix a is orthogonal if its transpose a t is also its inverse a − 1. Also, the product of an orthogonal matrix and its transpose is equal to i. When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix.. Orthogonal Matrix Def.
From www.slideserve.com
PPT Elementary Linear Algebra Anton & Rorres, 9 th Edition PowerPoint Orthogonal Matrix Def When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. A square matrix a is orthogonal if its transpose a t is also its inverse a − 1. An orthogonal matrix is a square matrix in which the rows and columns are mutually orthogonal unit vectors and. Orthogonal Matrix Def.