The Signal X(T)=Cos 4T Is at Terry Haskell blog

The Signal X(T)=Cos 4T Is. The frequency response of an lti system is shown below. For an input signal x (t) = cos (4t), what is output y (t)? Y (t)=0 y (t) = cos (4t)/2 y (t) = cos (4t) y (t) =. For each signal given below, determine the values of t for which it is guaranteed to be zero (if any). If the signal is periodic, determine its fundamental period. (a) x(4 t 2) (b)[x(t) + x( t)]u(t) (c) x(t)[. If a signal has e∞ as ∞ and p∞ as a finite value, then the signal is a power signal. If a signal has e∞ as a finite value and p ∞ as ∞, then the signal is an energy signal. Sketch and label carefully each of the following signals: The signal x(t) is neither even nor odd given that its values for t ≤ 0 are zero. There are 2 steps to solve this one. In summary, the problem is to find the value of t that makes the output of a system with impulse response h (t) equal to acos. Determine the fourier transform of each of the signals shown in figure 2. Let x(t) be a signal with x(t) =0 for t > 1. You should be able to do this by explicitly evaluating only the.

The frequency response of an lti system is shown below. The signal x(t) is neither even nor odd given that its values for t ≤ 0 are zero. Determine the fourier transform of each of the signals shown in figure 2. Y (t)=0 y (t) = cos (4t)/2 y (t) = cos (4t) y (t) =. For an input signal x (t) = cos (4t), what is output y (t)? If a signal has e∞ as ∞ and p∞ as a finite value, then the signal is a power signal. If a signal has e∞ as a finite value and p ∞ as ∞, then the signal is an energy signal. In summary, the problem is to find the value of t that makes the output of a system with impulse response h (t) equal to acos. There are 2 steps to solve this one. If the signal is periodic, determine its fundamental period.

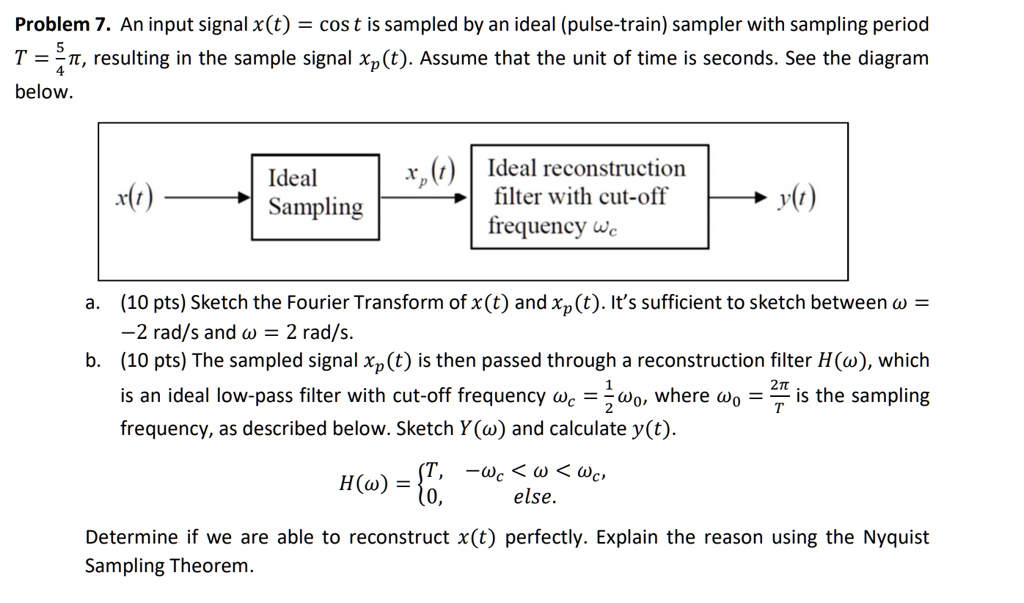
SOLVED Problem 7. An input signal x(t) = cos(t) is sampled by an ideal

The Signal X(T)=Cos 4T Is There are 2 steps to solve this one. For each signal given below, determine the values of t for which it is guaranteed to be zero (if any). Determine the fourier transform of each of the signals shown in figure 2. Sketch and label carefully each of the following signals: If a signal has e∞ as a finite value and p ∞ as ∞, then the signal is an energy signal. If the signal is periodic, determine its fundamental period. The frequency response of an lti system is shown below. In summary, the problem is to find the value of t that makes the output of a system with impulse response h (t) equal to acos. For an input signal x (t) = cos (4t), what is output y (t)? (a) x(4 t 2) (b)[x(t) + x( t)]u(t) (c) x(t)[. Y (t)=0 y (t) = cos (4t)/2 y (t) = cos (4t) y (t) =. The signal x(t) is neither even nor odd given that its values for t ≤ 0 are zero. You should be able to do this by explicitly evaluating only the. There are 2 steps to solve this one. Let x(t) be a signal with x(t) =0 for t > 1. If a signal has e∞ as ∞ and p∞ as a finite value, then the signal is a power signal.