What Is Orthogonal Matrix Example . A matrix a ∈ gl. That is, the following condition is met: Where a is an orthogonal. Learn more about the orthogonal. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every other row and column, and each row or column has a magnitude of 1. In other words, the product of a square orthogonal. Also, the product of an orthogonal matrix and its transpose is equal to i. N (r) is orthogonal if av · aw = v · w for all vectors v. Orthogonal matrices are those preserving the dot product. An orthogonal matrix is a square matrix with real numbers that multiplied by its transpose is equal to the identity matrix. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. A square matrix with real numbers or values is termed as an orthogonal matrix if its transpose is equal to the inverse matrix of it.
from datascienceparichay.com
Learn more about the orthogonal. That is, the following condition is met: N (r) is orthogonal if av · aw = v · w for all vectors v. Also, the product of an orthogonal matrix and its transpose is equal to i. Orthogonal matrices are those preserving the dot product. A square matrix with real numbers or values is termed as an orthogonal matrix if its transpose is equal to the inverse matrix of it. A matrix a ∈ gl. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. An orthogonal matrix is a square matrix with real numbers that multiplied by its transpose is equal to the identity matrix. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every other row and column, and each row or column has a magnitude of 1.
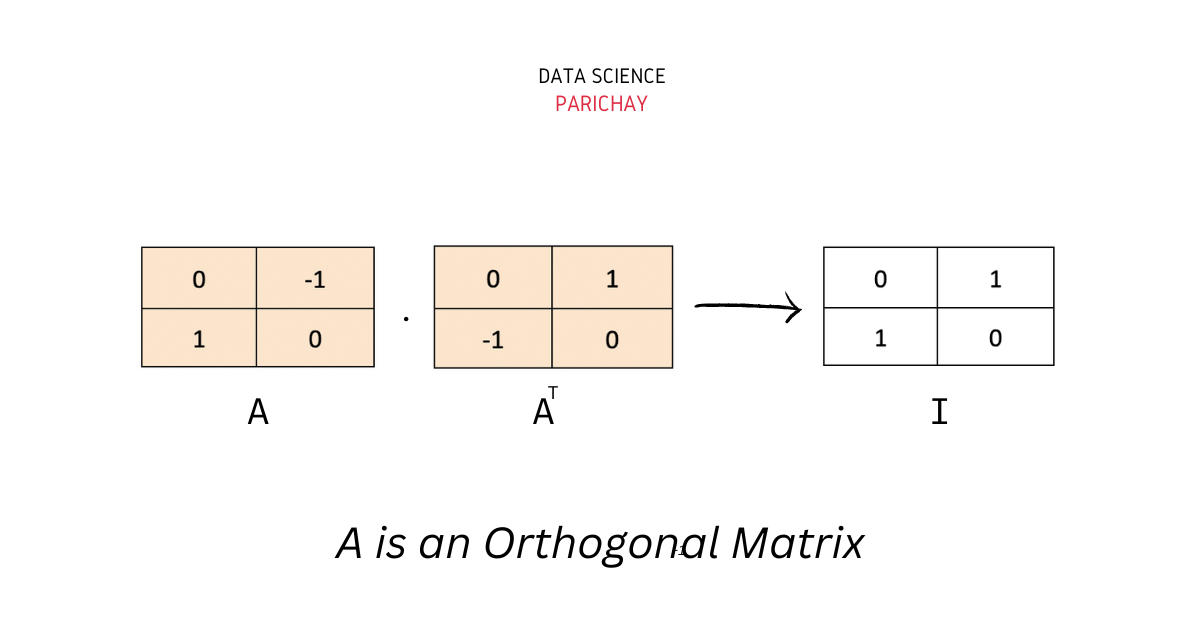
Numpy Check If a Matrix is Orthogonal Data Science Parichay
What Is Orthogonal Matrix Example A square matrix with real numbers or values is termed as an orthogonal matrix if its transpose is equal to the inverse matrix of it. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every other row and column, and each row or column has a magnitude of 1. Orthogonal matrices are those preserving the dot product. A square matrix with real numbers or values is termed as an orthogonal matrix if its transpose is equal to the inverse matrix of it. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. In other words, the product of a square orthogonal. A matrix a ∈ gl. Where a is an orthogonal. Learn more about the orthogonal. An orthogonal matrix is a square matrix with real numbers that multiplied by its transpose is equal to the identity matrix. N (r) is orthogonal if av · aw = v · w for all vectors v. That is, the following condition is met: Also, the product of an orthogonal matrix and its transpose is equal to i.
From slidetodoc.com
Chapter Content n n n Eigenvalues and Eigenvectors What Is Orthogonal Matrix Example A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. A matrix a ∈ gl. In other words, the product of a square orthogonal. Also, the product of an orthogonal matrix and its transpose is equal to i. A square matrix with real numbers or values is termed as an orthogonal matrix if its. What Is Orthogonal Matrix Example.
From www.youtube.com
Trick to find Inverse of (A.A^T) of Orthogonal Matrix GATE question What Is Orthogonal Matrix Example Learn more about the orthogonal. A matrix a ∈ gl. That is, the following condition is met: N (r) is orthogonal if av · aw = v · w for all vectors v. In other words, the product of a square orthogonal. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. An orthogonal. What Is Orthogonal Matrix Example.
From limfadreams.weebly.com
Orthogonal matrix limfadreams What Is Orthogonal Matrix Example In other words, the product of a square orthogonal. A square matrix with real numbers or values is termed as an orthogonal matrix if its transpose is equal to the inverse matrix of it. Orthogonal matrices are those preserving the dot product. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning. What Is Orthogonal Matrix Example.
From www.youtube.com
Orthogonal Matrix With Definition, Example and Properties YouTube What Is Orthogonal Matrix Example Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every other row and column, and each row or column has a magnitude of 1. That is, the following condition is met: Where a is an orthogonal. An orthogonal matrix is. What Is Orthogonal Matrix Example.
From klaxtukue.blob.core.windows.net
Orthogonal Matrix Theorems at Laura Yang blog What Is Orthogonal Matrix Example A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. N (r) is orthogonal if av · aw = v · w for all vectors v. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular. What Is Orthogonal Matrix Example.
From datascienceparichay.com
Numpy Check If a Matrix is Orthogonal Data Science Parichay What Is Orthogonal Matrix Example Where a is an orthogonal. A square matrix with real numbers or values is termed as an orthogonal matrix if its transpose is equal to the inverse matrix of it. An orthogonal matrix is a square matrix with real numbers that multiplied by its transpose is equal to the identity matrix. That is, the following condition is met: Learn more. What Is Orthogonal Matrix Example.
From www.youtube.com
Properties of Orthogonal Matrix Example1 YouTube What Is Orthogonal Matrix Example That is, the following condition is met: Where a is an orthogonal. An orthogonal matrix is a square matrix with real numbers that multiplied by its transpose is equal to the identity matrix. In other words, the product of a square orthogonal. Learn more about the orthogonal. Orthogonal matrix is a square matrix in which all rows and columns are. What Is Orthogonal Matrix Example.
From klazemyrp.blob.core.windows.net
How To Tell If A Matrix Is Orthogonal at Nancy Rameriz blog What Is Orthogonal Matrix Example Orthogonal matrices are those preserving the dot product. Also, the product of an orthogonal matrix and its transpose is equal to i. N (r) is orthogonal if av · aw = v · w for all vectors v. Where a is an orthogonal. Learn more about the orthogonal. An orthogonal matrix is a square matrix with real numbers that multiplied. What Is Orthogonal Matrix Example.
From www.youtube.com
Orthogonal Matrix What is orthogonal Matrix How to prove Orthogonal What Is Orthogonal Matrix Example Also, the product of an orthogonal matrix and its transpose is equal to i. Orthogonal matrices are those preserving the dot product. In other words, the product of a square orthogonal. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. N (r) is orthogonal if av · aw = v · w for. What Is Orthogonal Matrix Example.
From www.slideserve.com
PPT Matrices PowerPoint Presentation, free download ID1087200 What Is Orthogonal Matrix Example Also, the product of an orthogonal matrix and its transpose is equal to i. Where a is an orthogonal. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. That is, the following condition is met: Learn more about the orthogonal. N (r) is orthogonal if av · aw = v · w for. What Is Orthogonal Matrix Example.
From www.youtube.com
【Orthogonality】06 Orthogonal matrix YouTube What Is Orthogonal Matrix Example Learn more about the orthogonal. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every other row and column, and each row or column. What Is Orthogonal Matrix Example.
From www.slideserve.com
PPT ENGG2013 Unit 19 The principal axes theorem PowerPoint What Is Orthogonal Matrix Example Where a is an orthogonal. An orthogonal matrix is a square matrix with real numbers that multiplied by its transpose is equal to the identity matrix. Learn more about the orthogonal. Also, the product of an orthogonal matrix and its transpose is equal to i. N (r) is orthogonal if av · aw = v · w for all vectors. What Is Orthogonal Matrix Example.
From datingluda.weebly.com
Orthogonal matrix datingluda What Is Orthogonal Matrix Example A square matrix with real numbers or values is termed as an orthogonal matrix if its transpose is equal to the inverse matrix of it. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every other row and column, and. What Is Orthogonal Matrix Example.
From dxovlehoe.blob.core.windows.net
Example Orthogonal Matrix at Verena Cowan blog What Is Orthogonal Matrix Example In other words, the product of a square orthogonal. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every other row and column, and each row or column has a magnitude of 1. Also, the product of an orthogonal matrix. What Is Orthogonal Matrix Example.
From www.youtube.com
Orthogonal and Orthonormal Vectors Linear Algebra YouTube What Is Orthogonal Matrix Example N (r) is orthogonal if av · aw = v · w for all vectors v. A square matrix with real numbers or values is termed as an orthogonal matrix if its transpose is equal to the inverse matrix of it. A matrix a ∈ gl. That is, the following condition is met: Orthogonal matrix is a square matrix in. What Is Orthogonal Matrix Example.
From www.youtube.com
What is Orthogonal Matrix and its Properties Kamaldheeriya YouTube What Is Orthogonal Matrix Example Also, the product of an orthogonal matrix and its transpose is equal to i. N (r) is orthogonal if av · aw = v · w for all vectors v. A square matrix with real numbers or values is termed as an orthogonal matrix if its transpose is equal to the inverse matrix of it. Learn more about the orthogonal.. What Is Orthogonal Matrix Example.
From ar.inspiredpencil.com
3x3 Orthogonal Matrix What Is Orthogonal Matrix Example A square matrix with real numbers or values is termed as an orthogonal matrix if its transpose is equal to the inverse matrix of it. In other words, the product of a square orthogonal. Orthogonal matrices are those preserving the dot product. That is, the following condition is met: Also, the product of an orthogonal matrix and its transpose is. What Is Orthogonal Matrix Example.
From eduinput.com
What is an Orthogonal Matrix?Example of Orthogonal Matrix What Is Orthogonal Matrix Example Where a is an orthogonal. That is, the following condition is met: Also, the product of an orthogonal matrix and its transpose is equal to i. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. Orthogonal matrices are those preserving the dot product. Orthogonal matrix is a square matrix in which all rows. What Is Orthogonal Matrix Example.
From klazemyrp.blob.core.windows.net
How To Tell If A Matrix Is Orthogonal at Nancy Rameriz blog What Is Orthogonal Matrix Example A matrix a ∈ gl. Also, the product of an orthogonal matrix and its transpose is equal to i. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every other row and column, and each row or column has a. What Is Orthogonal Matrix Example.
From www.slideserve.com
PPT ENGG2013 Unit 19 The principal axes theorem PowerPoint What Is Orthogonal Matrix Example That is, the following condition is met: Where a is an orthogonal. Orthogonal matrices are those preserving the dot product. A matrix a ∈ gl. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. A square matrix with real numbers or values is termed as an orthogonal matrix if its transpose is equal. What Is Orthogonal Matrix Example.
From gateoverflow.in
Linear Algebra Engineering Maths Orthogonal Matrix What Is Orthogonal Matrix Example Learn more about the orthogonal. Where a is an orthogonal. That is, the following condition is met: Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every other row and column, and each row or column has a magnitude of. What Is Orthogonal Matrix Example.
From www.youtube.com
Orthogonal Matrix Definition Example Properties Class 12 Maths YouTube What Is Orthogonal Matrix Example Where a is an orthogonal. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. A square matrix with real numbers or values is termed as an orthogonal matrix if its transpose is equal to the inverse matrix of it. In other words, the product of a square orthogonal. Learn more about the orthogonal.. What Is Orthogonal Matrix Example.
From www.slideserve.com
PPT Projection Matrices PowerPoint Presentation, free download ID What Is Orthogonal Matrix Example N (r) is orthogonal if av · aw = v · w for all vectors v. A matrix a ∈ gl. A square matrix with real numbers or values is termed as an orthogonal matrix if its transpose is equal to the inverse matrix of it. An orthogonal matrix is a square matrix with real numbers that multiplied by its. What Is Orthogonal Matrix Example.
From study.com
Orthogonal Vectors Overview, Formula & Examples Lesson What Is Orthogonal Matrix Example Learn more about the orthogonal. Where a is an orthogonal. A square matrix with real numbers or values is termed as an orthogonal matrix if its transpose is equal to the inverse matrix of it. In other words, the product of a square orthogonal. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit. What Is Orthogonal Matrix Example.
From klaujekhl.blob.core.windows.net
How To Generate Orthogonal Matrix In Matlab at Kara Watson blog What Is Orthogonal Matrix Example That is, the following condition is met: Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every other row and column, and each row or column has a magnitude of 1. Learn more about the orthogonal. A square matrix with. What Is Orthogonal Matrix Example.
From www.youtube.com
Orthogonal Matrix example YouTube What Is Orthogonal Matrix Example Learn more about the orthogonal. Where a is an orthogonal. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. N (r) is orthogonal if av · aw = v · w for all vectors v. A matrix a ∈ gl. That is, the following condition is met: A square matrix with real numbers. What Is Orthogonal Matrix Example.
From inputone.weebly.com
inputone Blog What Is Orthogonal Matrix Example Where a is an orthogonal. Orthogonal matrices are those preserving the dot product. An orthogonal matrix is a square matrix with real numbers that multiplied by its transpose is equal to the identity matrix. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix. What Is Orthogonal Matrix Example.
From www.youtube.com
Orthonormal,Orthogonal matrix (EE MATH มทส.) YouTube What Is Orthogonal Matrix Example A matrix a ∈ gl. In other words, the product of a square orthogonal. A square matrix with real numbers or values is termed as an orthogonal matrix if its transpose is equal to the inverse matrix of it. Also, the product of an orthogonal matrix and its transpose is equal to i. Where a is an orthogonal. A matrix. What Is Orthogonal Matrix Example.
From www.slideserve.com
PPT Orthogonal matrices PowerPoint Presentation, free download ID What Is Orthogonal Matrix Example N (r) is orthogonal if av · aw = v · w for all vectors v. Also, the product of an orthogonal matrix and its transpose is equal to i. Orthogonal matrices are those preserving the dot product. An orthogonal matrix is a square matrix with real numbers that multiplied by its transpose is equal to the identity matrix. Learn. What Is Orthogonal Matrix Example.
From www.slideserve.com
PPT 6.4 Best Approximation; Least Squares PowerPoint Presentation What Is Orthogonal Matrix Example In other words, the product of a square orthogonal. N (r) is orthogonal if av · aw = v · w for all vectors v. A matrix a ∈ gl. An orthogonal matrix is a square matrix with real numbers that multiplied by its transpose is equal to the identity matrix. Where a is an orthogonal. Orthogonal matrix is a. What Is Orthogonal Matrix Example.
From 911weknow.com
[Linear Algebra] 9. Properties of orthogonal matrices 911 WeKnow What Is Orthogonal Matrix Example Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every other row and column, and each row or column has a magnitude of 1. Orthogonal matrices are those preserving the dot product. In other words, the product of a square. What Is Orthogonal Matrix Example.
From www.slideserve.com
PPT Row and column matrices are sometimes called row vectors and What Is Orthogonal Matrix Example Also, the product of an orthogonal matrix and its transpose is equal to i. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. Where a is an orthogonal. Learn more about the orthogonal. That is, the following condition is met: Orthogonal matrices are those preserving the dot product. A square matrix with real. What Is Orthogonal Matrix Example.
From www.youtube.com
How to Prove that a Matrix is Orthogonal YouTube What Is Orthogonal Matrix Example Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every other row and column, and each row or column has a magnitude of 1. An orthogonal matrix is a square matrix with real numbers that multiplied by its transpose is. What Is Orthogonal Matrix Example.
From slideplayer.com
Orthogonal Matrices & Symmetric Matrices ppt download What Is Orthogonal Matrix Example Where a is an orthogonal. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every other row and column, and each row or column has a magnitude of 1. Orthogonal matrices are those preserving the dot product. An orthogonal matrix. What Is Orthogonal Matrix Example.
From www.youtube.com
MATRICES (L3) LINEAR TRANSFORMATIONORTHOGONAL MATRIX YouTube What Is Orthogonal Matrix Example Also, the product of an orthogonal matrix and its transpose is equal to i. In other words, the product of a square orthogonal. Where a is an orthogonal. That is, the following condition is met: An orthogonal matrix is a square matrix with real numbers that multiplied by its transpose is equal to the identity matrix. A square matrix with. What Is Orthogonal Matrix Example.