In How Many Ways Can 5 Balls Be Placed In 3 Boxes . Thus the total number of arrangements for 3 indistinguishable boxes and 5 distinguishable balls is $1 + 5 + 10 + 10 + 15 = \boxed{41}$. But for this type of problem it works very nicely. So there are 6 triplets and hence 6 numbers of ways to place 5 identical balls in 3 identical boxes. If no box remains empty, then we can have (1,1,3) or (1,2,2) distribution pattern. When balls are different and boxes are identical,. Each box can hold all the five balls. Five balls are placed in three boxes. In how many different ways can we place the balls in the. We can alternatively find number of. When balls as well as boxes are identical, we have. Three balls in one box and one ball in each of the others: If no box remains empty, then we can have (1, 1, 3) or (1,2,2) distribution pattern. That can also be computationally tedious. (a) each box (say b1,b2,b3 ) will have at least one ball. There are three ways to choose which box receives three balls, (5 3).
from www.teachoo.com
If no box remains empty, then we can have (1,1,3) or (1,2,2) distribution pattern. Thus the total number of arrangements for 3 indistinguishable boxes and 5 distinguishable balls is $1 + 5 + 10 + 10 + 15 = \boxed{41}$. (a) each box (say b1,b2,b3 ) will have at least one ball. When balls as well as boxes are identical, we have. Five balls are placed in three boxes. So there are 6 triplets and hence 6 numbers of ways to place 5 identical balls in 3 identical boxes. When balls are different and boxes are identical,. But for this type of problem it works very nicely. We can alternatively find number of. Each box can hold all the five balls.
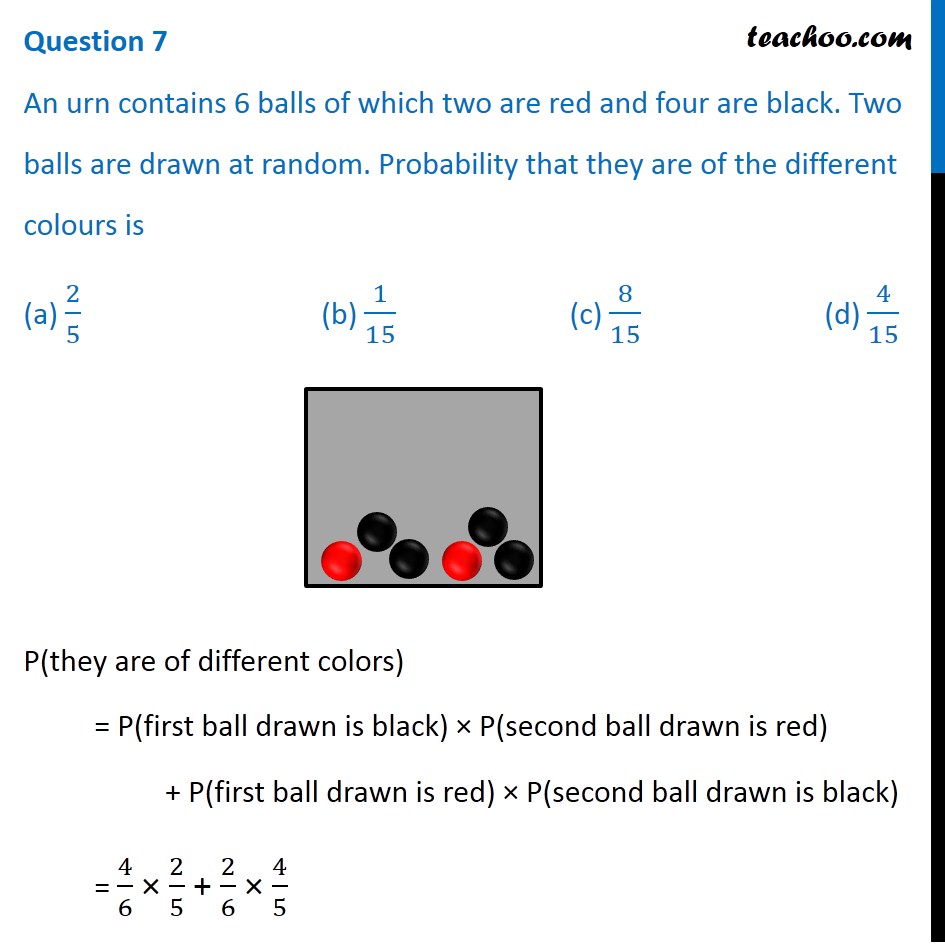
An urn contains 6 balls of which two are red and four are black
In How Many Ways Can 5 Balls Be Placed In 3 Boxes When balls are different and boxes are identical,. There are three ways to choose which box receives three balls, (5 3). Three balls in one box and one ball in each of the others: When balls are different and boxes are identical,. That can also be computationally tedious. Five balls are placed in three boxes. If no box remains empty, then we can have (1,1,3) or (1,2,2) distribution pattern. If no box remains empty, then we can have (1, 1, 3) or (1,2,2) distribution pattern. We can alternatively find number of. When balls as well as boxes are identical, we have. In how many different ways can we place the balls in the. (a) each box (say b1,b2,b3 ) will have at least one ball. Thus the total number of arrangements for 3 indistinguishable boxes and 5 distinguishable balls is $1 + 5 + 10 + 10 + 15 = \boxed{41}$. So there are 6 triplets and hence 6 numbers of ways to place 5 identical balls in 3 identical boxes. But for this type of problem it works very nicely. Each box can hold all the five balls.
From www.toppr.com
In how many ways 5 different balls can be distributed into 3 boxes so In How Many Ways Can 5 Balls Be Placed In 3 Boxes If no box remains empty, then we can have (1,1,3) or (1,2,2) distribution pattern. Each box can hold all the five balls. Five balls are placed in three boxes. When balls are different and boxes are identical,. That can also be computationally tedious. In how many different ways can we place the balls in the. (a) each box (say b1,b2,b3. In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From www.vrogue.co
A Box Contains 5 Red Balls And 3 Blue Balls Are Drawn vrogue.co In How Many Ways Can 5 Balls Be Placed In 3 Boxes (a) each box (say b1,b2,b3 ) will have at least one ball. Three balls in one box and one ball in each of the others: In how many different ways can we place the balls in the. There are three ways to choose which box receives three balls, (5 3). So there are 6 triplets and hence 6 numbers of. In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From www.youtube.com
5 balls are to be placed in 3 boxes. Each box can hold all the 5 balls In How Many Ways Can 5 Balls Be Placed In 3 Boxes So there are 6 triplets and hence 6 numbers of ways to place 5 identical balls in 3 identical boxes. Three balls in one box and one ball in each of the others: When balls are different and boxes are identical,. When balls as well as boxes are identical, we have. (a) each box (say b1,b2,b3 ) will have at. In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From edurev.in
There are two boxes containing 5 white and 6 blue balls and 3 white and In How Many Ways Can 5 Balls Be Placed In 3 Boxes When balls as well as boxes are identical, we have. Each box can hold all the five balls. If no box remains empty, then we can have (1,1,3) or (1,2,2) distribution pattern. There are three ways to choose which box receives three balls, (5 3). Five balls are placed in three boxes. Thus the total number of arrangements for 3. In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From www.gauthmath.com
Solved 3.In how many ways can 5 people arrange themselves in a row for In How Many Ways Can 5 Balls Be Placed In 3 Boxes That can also be computationally tedious. Each box can hold all the five balls. Five balls are placed in three boxes. When balls as well as boxes are identical, we have. If no box remains empty, then we can have (1, 1, 3) or (1,2,2) distribution pattern. Thus the total number of arrangements for 3 indistinguishable boxes and 5 distinguishable. In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From www.youtube.com
Lecture1 Distribution of n identical/distinct Balls into r identical In How Many Ways Can 5 Balls Be Placed In 3 Boxes We can alternatively find number of. When balls as well as boxes are identical, we have. Three balls in one box and one ball in each of the others: That can also be computationally tedious. If no box remains empty, then we can have (1, 1, 3) or (1,2,2) distribution pattern. When balls are different and boxes are identical,. (a). In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From www.teachoo.com
Ex 15.1, 8 A bag contains 3 red balls and 5 black balls In How Many Ways Can 5 Balls Be Placed In 3 Boxes There are three ways to choose which box receives three balls, (5 3). That can also be computationally tedious. If no box remains empty, then we can have (1, 1, 3) or (1,2,2) distribution pattern. We can alternatively find number of. (a) each box (say b1,b2,b3 ) will have at least one ball. In how many different ways can we. In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From www.youtube.com
Counting the number of ways to place identical balls in distinct bins In How Many Ways Can 5 Balls Be Placed In 3 Boxes In how many different ways can we place the balls in the. That can also be computationally tedious. If no box remains empty, then we can have (1,1,3) or (1,2,2) distribution pattern. When balls are different and boxes are identical,. (a) each box (say b1,b2,b3 ) will have at least one ball. Thus the total number of arrangements for 3. In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From www.teachoo.com
An urn contains 6 balls of which two are red and four are black In How Many Ways Can 5 Balls Be Placed In 3 Boxes In how many different ways can we place the balls in the. (a) each box (say b1,b2,b3 ) will have at least one ball. Each box can hold all the five balls. But for this type of problem it works very nicely. So there are 6 triplets and hence 6 numbers of ways to place 5 identical balls in 3. In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From www.youtube.com
Find the number of ways of selecting 9 balls from 6 red balls 5 white In How Many Ways Can 5 Balls Be Placed In 3 Boxes Three balls in one box and one ball in each of the others: If no box remains empty, then we can have (1,1,3) or (1,2,2) distribution pattern. In how many different ways can we place the balls in the. That can also be computationally tedious. If no box remains empty, then we can have (1, 1, 3) or (1,2,2) distribution. In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From www.vrogue.co
A Box Contains 5 Red Balls And 3 Blue Balls Are Drawn vrogue.co In How Many Ways Can 5 Balls Be Placed In 3 Boxes If no box remains empty, then we can have (1, 1, 3) or (1,2,2) distribution pattern. Three balls in one box and one ball in each of the others: So there are 6 triplets and hence 6 numbers of ways to place 5 identical balls in 3 identical boxes. (a) each box (say b1,b2,b3 ) will have at least one. In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From www.teachoo.com
Example 24 In how many ways can 5 girls and 3 boys be seated In How Many Ways Can 5 Balls Be Placed In 3 Boxes If no box remains empty, then we can have (1,1,3) or (1,2,2) distribution pattern. (a) each box (say b1,b2,b3 ) will have at least one ball. When balls are different and boxes are identical,. In how many different ways can we place the balls in the. Thus the total number of arrangements for 3 indistinguishable boxes and 5 distinguishable balls. In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From math.stackexchange.com
combinatorics If 12 distinct balls are to be placed in 3 In How Many Ways Can 5 Balls Be Placed In 3 Boxes So there are 6 triplets and hence 6 numbers of ways to place 5 identical balls in 3 identical boxes. Thus the total number of arrangements for 3 indistinguishable boxes and 5 distinguishable balls is $1 + 5 + 10 + 10 + 15 = \boxed{41}$. If no box remains empty, then we can have (1,1,3) or (1,2,2) distribution pattern.. In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From www.toppr.com
In how many ways can 5 identical balls be arranged in 3 boxes? In How Many Ways Can 5 Balls Be Placed In 3 Boxes So there are 6 triplets and hence 6 numbers of ways to place 5 identical balls in 3 identical boxes. (a) each box (say b1,b2,b3 ) will have at least one ball. If no box remains empty, then we can have (1, 1, 3) or (1,2,2) distribution pattern. When balls as well as boxes are identical, we have. But for. In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From www.vrogue.co
Solved Bag Contains 4 Red Balls And 5 Blue Balls Rahe vrogue.co In How Many Ways Can 5 Balls Be Placed In 3 Boxes That can also be computationally tedious. Each box can hold all the five balls. In how many different ways can we place the balls in the. Three balls in one box and one ball in each of the others: Thus the total number of arrangements for 3 indistinguishable boxes and 5 distinguishable balls is $1 + 5 + 10 +. In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From www.toppr.com
In how many ways 5 different balls can be distributed into 3 boxes so In How Many Ways Can 5 Balls Be Placed In 3 Boxes We can alternatively find number of. That can also be computationally tedious. There are three ways to choose which box receives three balls, (5 3). In how many different ways can we place the balls in the. Each box can hold all the five balls. Thus the total number of arrangements for 3 indistinguishable boxes and 5 distinguishable balls is. In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From www.youtube.com
Balls into Boxes Permutations and Combinations Lesson YouTube In How Many Ways Can 5 Balls Be Placed In 3 Boxes In how many different ways can we place the balls in the. If no box remains empty, then we can have (1,1,3) or (1,2,2) distribution pattern. If no box remains empty, then we can have (1, 1, 3) or (1,2,2) distribution pattern. When balls are different and boxes are identical,. We can alternatively find number of. Thus the total number. In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From www.demonstrations.wolfram.com
Arranging Balls into Boxes Wolfram Demonstrations Project In How Many Ways Can 5 Balls Be Placed In 3 Boxes If no box remains empty, then we can have (1,1,3) or (1,2,2) distribution pattern. Each box can hold all the five balls. If no box remains empty, then we can have (1, 1, 3) or (1,2,2) distribution pattern. When balls are different and boxes are identical,. (a) each box (say b1,b2,b3 ) will have at least one ball. Three balls. In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From www.learnpick.in
A bag contains 7 red and 5 white balls,2 balls are drawn at random In How Many Ways Can 5 Balls Be Placed In 3 Boxes There are three ways to choose which box receives three balls, (5 3). If no box remains empty, then we can have (1,1,3) or (1,2,2) distribution pattern. When balls are different and boxes are identical,. Three balls in one box and one ball in each of the others: When balls as well as boxes are identical, we have. In how. In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From portal.dzp.pl
In A Box There Are 100 Balls Of Different Colors ENSINO In How Many Ways Can 5 Balls Be Placed In 3 Boxes Three balls in one box and one ball in each of the others: So there are 6 triplets and hence 6 numbers of ways to place 5 identical balls in 3 identical boxes. When balls are different and boxes are identical,. But for this type of problem it works very nicely. That can also be computationally tedious. There are three. In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From www.numerade.com
SOLVED . A box contains 2 white balls, 3 black balls and 4 red balls In How Many Ways Can 5 Balls Be Placed In 3 Boxes When balls as well as boxes are identical, we have. If no box remains empty, then we can have (1, 1, 3) or (1,2,2) distribution pattern. Each box can hold all the five balls. Thus the total number of arrangements for 3 indistinguishable boxes and 5 distinguishable balls is $1 + 5 + 10 + 10 + 15 = \boxed{41}$.. In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From brainly.in
A bag contains 5 white 6 red and 4 green balls one ball is drawn In How Many Ways Can 5 Balls Be Placed In 3 Boxes In how many different ways can we place the balls in the. Each box can hold all the five balls. Three balls in one box and one ball in each of the others: When balls as well as boxes are identical, we have. That can also be computationally tedious. If no box remains empty, then we can have (1, 1,. In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From www.teachoo.com
Example 8 A box contains 3 blue, 2 white and 4 red marbles In How Many Ways Can 5 Balls Be Placed In 3 Boxes If no box remains empty, then we can have (1,1,3) or (1,2,2) distribution pattern. When balls are different and boxes are identical,. But for this type of problem it works very nicely. Each box can hold all the five balls. We can alternatively find number of. Three balls in one box and one ball in each of the others: If. In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From www.slideserve.com
PPT Lecture 6 PowerPoint Presentation, free download ID4724070 In How Many Ways Can 5 Balls Be Placed In 3 Boxes Each box can hold all the five balls. But for this type of problem it works very nicely. Five balls are placed in three boxes. Three balls in one box and one ball in each of the others: (a) each box (say b1,b2,b3 ) will have at least one ball. If no box remains empty, then we can have (1,1,3). In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From www.toppr.com
Number of ways of placing 5 different balls in 3 identical boxes (no In How Many Ways Can 5 Balls Be Placed In 3 Boxes Three balls in one box and one ball in each of the others: So there are 6 triplets and hence 6 numbers of ways to place 5 identical balls in 3 identical boxes. Thus the total number of arrangements for 3 indistinguishable boxes and 5 distinguishable balls is $1 + 5 + 10 + 10 + 15 = \boxed{41}$. (a). In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From www.teachoo.com
Example 24 In how many ways can 5 girls and 3 boys be seated In How Many Ways Can 5 Balls Be Placed In 3 Boxes If no box remains empty, then we can have (1, 1, 3) or (1,2,2) distribution pattern. Five balls are placed in three boxes. So there are 6 triplets and hence 6 numbers of ways to place 5 identical balls in 3 identical boxes. (a) each box (say b1,b2,b3 ) will have at least one ball. That can also be computationally. In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From edurev.in
A box contains 5 white and 7 black balls. two successive drawn of 3 In How Many Ways Can 5 Balls Be Placed In 3 Boxes Each box can hold all the five balls. There are three ways to choose which box receives three balls, (5 3). That can also be computationally tedious. Five balls are placed in three boxes. If no box remains empty, then we can have (1,1,3) or (1,2,2) distribution pattern. But for this type of problem it works very nicely. In how. In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From www.teachoo.com
Ex 6.4, 5 Find number of ways of selecting 9 balls from 6 In How Many Ways Can 5 Balls Be Placed In 3 Boxes When balls as well as boxes are identical, we have. Each box can hold all the five balls. We can alternatively find number of. But for this type of problem it works very nicely. If no box remains empty, then we can have (1, 1, 3) or (1,2,2) distribution pattern. (a) each box (say b1,b2,b3 ) will have at least. In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From www.teachoo.com
A bag contains 3 red balls, 5 white balls and 7 black balls MCQ In How Many Ways Can 5 Balls Be Placed In 3 Boxes Three balls in one box and one ball in each of the others: That can also be computationally tedious. Thus the total number of arrangements for 3 indistinguishable boxes and 5 distinguishable balls is $1 + 5 + 10 + 10 + 15 = \boxed{41}$. We can alternatively find number of. (a) each box (say b1,b2,b3 ) will have at. In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From ifunny.co
There are three boxes. Each box contains 2 balls. One box contains 2 In How Many Ways Can 5 Balls Be Placed In 3 Boxes So there are 6 triplets and hence 6 numbers of ways to place 5 identical balls in 3 identical boxes. Three balls in one box and one ball in each of the others: We can alternatively find number of. When balls are different and boxes are identical,. Five balls are placed in three boxes. There are three ways to choose. In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From www.toppr.com
5 balls are to be placed in 3 boxes. Each box can hold all the 5 balls In How Many Ways Can 5 Balls Be Placed In 3 Boxes So there are 6 triplets and hence 6 numbers of ways to place 5 identical balls in 3 identical boxes. If no box remains empty, then we can have (1, 1, 3) or (1,2,2) distribution pattern. In how many different ways can we place the balls in the. Thus the total number of arrangements for 3 indistinguishable boxes and 5. In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From www.toppr.com
The number of ways 5 identical balls can be distributed into 3 In How Many Ways Can 5 Balls Be Placed In 3 Boxes Five balls are placed in three boxes. So there are 6 triplets and hence 6 numbers of ways to place 5 identical balls in 3 identical boxes. But for this type of problem it works very nicely. There are three ways to choose which box receives three balls, (5 3). If no box remains empty, then we can have (1,. In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From www.baamboozle.com
LET´S PRACTICE!!! Baamboozle In How Many Ways Can 5 Balls Be Placed In 3 Boxes Thus the total number of arrangements for 3 indistinguishable boxes and 5 distinguishable balls is $1 + 5 + 10 + 10 + 15 = \boxed{41}$. When balls are different and boxes are identical,. (a) each box (say b1,b2,b3 ) will have at least one ball. Each box can hold all the five balls. That can also be computationally tedious.. In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From www.teachoo.com
Ex 6.4, 8 A bag contains 5 black and 6 red balls. Determine In How Many Ways Can 5 Balls Be Placed In 3 Boxes Thus the total number of arrangements for 3 indistinguishable boxes and 5 distinguishable balls is $1 + 5 + 10 + 10 + 15 = \boxed{41}$. Three balls in one box and one ball in each of the others: When balls are different and boxes are identical,. (a) each box (say b1,b2,b3 ) will have at least one ball. We. In How Many Ways Can 5 Balls Be Placed In 3 Boxes.
From www.toppr.com
"13. Five balls of different colours are to be.nplaced in three boxes In How Many Ways Can 5 Balls Be Placed In 3 Boxes Thus the total number of arrangements for 3 indistinguishable boxes and 5 distinguishable balls is $1 + 5 + 10 + 10 + 15 = \boxed{41}$. There are three ways to choose which box receives three balls, (5 3). (a) each box (say b1,b2,b3 ) will have at least one ball. When balls as well as boxes are identical, we. In How Many Ways Can 5 Balls Be Placed In 3 Boxes.