Distribution Of Sample Variance Of Normal . Assuming $n$ samples $\{x_1,.,x_n\}$ are taken from a normal distribution with mean $\mu$ and variance $\sigma^2$, then the variance can be. \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). If an arbitrarily large number of samples, each involving multiple observations (data points), were separately used in order to compute one value. Theorem 7.2.3 states that the distribution of the sample variance, when sampling from a normally distributed. \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). Consider a distribution with mean $\mu$, variance $\sigma^2$, skewness $\gamma$ and kurtosis $\kappa$ (where all these moments are finite).
from www.numerade.com
Consider a distribution with mean $\mu$, variance $\sigma^2$, skewness $\gamma$ and kurtosis $\kappa$ (where all these moments are finite). \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). If an arbitrarily large number of samples, each involving multiple observations (data points), were separately used in order to compute one value. Theorem 7.2.3 states that the distribution of the sample variance, when sampling from a normally distributed. Assuming $n$ samples $\{x_1,.,x_n\}$ are taken from a normal distribution with mean $\mu$ and variance $\sigma^2$, then the variance can be.
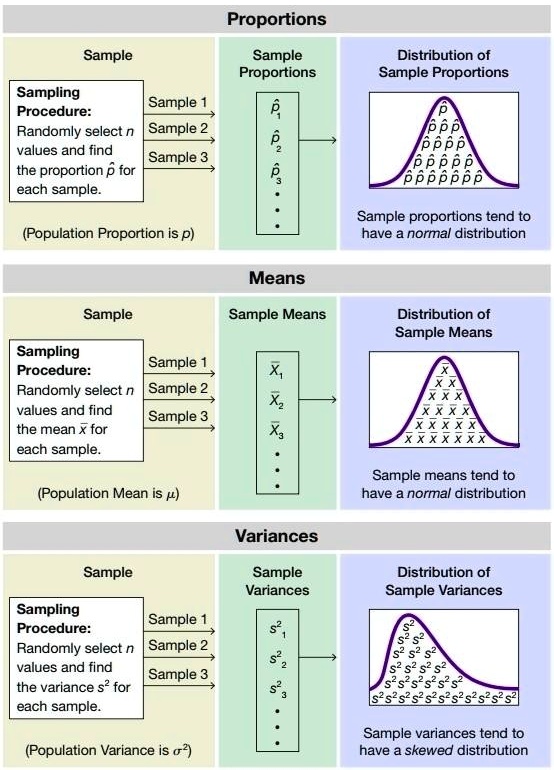
SOLVED Please explain this chart. Proportions Sample Sample
Distribution Of Sample Variance Of Normal \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). Consider a distribution with mean $\mu$, variance $\sigma^2$, skewness $\gamma$ and kurtosis $\kappa$ (where all these moments are finite). \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). If an arbitrarily large number of samples, each involving multiple observations (data points), were separately used in order to compute one value. Assuming $n$ samples $\{x_1,.,x_n\}$ are taken from a normal distribution with mean $\mu$ and variance $\sigma^2$, then the variance can be. Theorem 7.2.3 states that the distribution of the sample variance, when sampling from a normally distributed.
From www.researchgate.net
Two normal distributions with different variances and equal means Distribution Of Sample Variance Of Normal \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). Consider a distribution with mean $\mu$, variance $\sigma^2$, skewness $\gamma$ and kurtosis $\kappa$ (where all these moments are finite). Theorem 7.2.3 states. Distribution Of Sample Variance Of Normal.
From mathsathome.com
How to Calculate Variance Distribution Of Sample Variance Of Normal \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). If an arbitrarily large number of samples, each involving multiple observations (data points), were separately used in order to compute one value. Theorem 7.2.3 states that the distribution of the sample variance, when sampling from a normally distributed. \(x_1, x_2, \ldots,. Distribution Of Sample Variance Of Normal.
From curvebreakerstestprep.com
Standard Deviation Variation from the Mean Curvebreakers Distribution Of Sample Variance Of Normal Theorem 7.2.3 states that the distribution of the sample variance, when sampling from a normally distributed. \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). If an arbitrarily large number of samples, each involving multiple observations (data points), were separately used in order to compute one value. \(x_1, x_2, \ldots,. Distribution Of Sample Variance Of Normal.
From www.reddit.com
My attempt to explain Stable Diffusion at a ELI15 level r/StableDiffusion Distribution Of Sample Variance Of Normal Theorem 7.2.3 states that the distribution of the sample variance, when sampling from a normally distributed. If an arbitrarily large number of samples, each involving multiple observations (data points), were separately used in order to compute one value. Consider a distribution with mean $\mu$, variance $\sigma^2$, skewness $\gamma$ and kurtosis $\kappa$ (where all these moments are finite). \(x_1, x_2, \ldots,. Distribution Of Sample Variance Of Normal.
From www.youtube.com
Proof Sampling Variance Relationship to the ChiSquared Distribution Distribution Of Sample Variance Of Normal \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). Assuming $n$ samples $\{x_1,.,x_n\}$ are taken from a normal distribution with mean $\mu$ and variance $\sigma^2$, then the variance can be. If an arbitrarily large number of samples, each involving multiple observations (data points), were separately used in order to compute. Distribution Of Sample Variance Of Normal.
From www.thoughtco.com
How to Calculate a Sample Standard Deviation Distribution Of Sample Variance Of Normal If an arbitrarily large number of samples, each involving multiple observations (data points), were separately used in order to compute one value. Consider a distribution with mean $\mu$, variance $\sigma^2$, skewness $\gamma$ and kurtosis $\kappa$ (where all these moments are finite). Assuming $n$ samples $\{x_1,.,x_n\}$ are taken from a normal distribution with mean $\mu$ and variance $\sigma^2$, then the variance. Distribution Of Sample Variance Of Normal.
From www.slideserve.com
PPT Measures of Dispersion PowerPoint Presentation ID228870 Distribution Of Sample Variance Of Normal \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). Theorem 7.2.3 states that the distribution of the sample variance, when sampling from a normally distributed. Consider a distribution with mean $\mu$, variance $\sigma^2$, skewness $\gamma$ and kurtosis $\kappa$ (where all these moments are finite). \(x_1, x_2, \ldots, x_n\) are observations. Distribution Of Sample Variance Of Normal.
From www.numerade.com
SOLVED Please explain this chart. Proportions Sample Sample Distribution Of Sample Variance Of Normal Theorem 7.2.3 states that the distribution of the sample variance, when sampling from a normally distributed. Assuming $n$ samples $\{x_1,.,x_n\}$ are taken from a normal distribution with mean $\mu$ and variance $\sigma^2$, then the variance can be. \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). Consider a distribution with. Distribution Of Sample Variance Of Normal.
From www.youtube.com
Standard Deviation and Variance for the Standard Normal Distribution Distribution Of Sample Variance Of Normal Consider a distribution with mean $\mu$, variance $\sigma^2$, skewness $\gamma$ and kurtosis $\kappa$ (where all these moments are finite). Assuming $n$ samples $\{x_1,.,x_n\}$ are taken from a normal distribution with mean $\mu$ and variance $\sigma^2$, then the variance can be. \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). If. Distribution Of Sample Variance Of Normal.
From www.kristakingmath.com
How to find Mean, variance, and standard deviation — Krista King Math Distribution Of Sample Variance Of Normal Theorem 7.2.3 states that the distribution of the sample variance, when sampling from a normally distributed. \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). If an arbitrarily large number of samples, each involving multiple observations (data points), were separately used in order to compute one value. Assuming $n$ samples. Distribution Of Sample Variance Of Normal.
From smartadm.ru
Estimating the error variance • Smartadm.ru Distribution Of Sample Variance Of Normal \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). Theorem 7.2.3 states that the distribution of the sample variance, when sampling from a normally distributed. \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). Assuming $n$ samples $\{x_1,.,x_n\}$ are taken. Distribution Of Sample Variance Of Normal.
From www.slideserve.com
PPT Statistical Theory; Why is the Gaussian Distribution so popular Distribution Of Sample Variance Of Normal Theorem 7.2.3 states that the distribution of the sample variance, when sampling from a normally distributed. Assuming $n$ samples $\{x_1,.,x_n\}$ are taken from a normal distribution with mean $\mu$ and variance $\sigma^2$, then the variance can be. \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). \(x_1, x_2, \ldots, x_n\). Distribution Of Sample Variance Of Normal.
From www.teachoo.com
Example 10 Calculate mean, variance, standard deviation Distribution Of Sample Variance Of Normal Assuming $n$ samples $\{x_1,.,x_n\}$ are taken from a normal distribution with mean $\mu$ and variance $\sigma^2$, then the variance can be. Theorem 7.2.3 states that the distribution of the sample variance, when sampling from a normally distributed. \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). \(x_1, x_2, \ldots, x_n\). Distribution Of Sample Variance Of Normal.
From www.slideserve.com
PPT Normal Probability Distributions PowerPoint Presentation, free Distribution Of Sample Variance Of Normal Consider a distribution with mean $\mu$, variance $\sigma^2$, skewness $\gamma$ and kurtosis $\kappa$ (where all these moments are finite). Theorem 7.2.3 states that the distribution of the sample variance, when sampling from a normally distributed. \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). If an arbitrarily large number of. Distribution Of Sample Variance Of Normal.
From statisticsglobe.com
Variance in R (3 Examples) Apply var Function with R Studio Distribution Of Sample Variance Of Normal If an arbitrarily large number of samples, each involving multiple observations (data points), were separately used in order to compute one value. Theorem 7.2.3 states that the distribution of the sample variance, when sampling from a normally distributed. Assuming $n$ samples $\{x_1,.,x_n\}$ are taken from a normal distribution with mean $\mu$ and variance $\sigma^2$, then the variance can be. \(x_1,. Distribution Of Sample Variance Of Normal.
From www.chegg.com
Solved Example 1 Sample Variance Let X, X,., x, be a Distribution Of Sample Variance Of Normal If an arbitrarily large number of samples, each involving multiple observations (data points), were separately used in order to compute one value. \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). Theorem 7.2.3 states that the distribution of the sample variance, when sampling from a normally distributed. \(x_1, x_2, \ldots,. Distribution Of Sample Variance Of Normal.
From www.scribbr.com
The Standard Normal Distribution Examples, Explanations, Uses Distribution Of Sample Variance Of Normal If an arbitrarily large number of samples, each involving multiple observations (data points), were separately used in order to compute one value. Theorem 7.2.3 states that the distribution of the sample variance, when sampling from a normally distributed. Assuming $n$ samples $\{x_1,.,x_n\}$ are taken from a normal distribution with mean $\mu$ and variance $\sigma^2$, then the variance can be. \(x_1,. Distribution Of Sample Variance Of Normal.
From www.slideserve.com
PPT Chapter 11 PowerPoint Presentation, free download ID424885 Distribution Of Sample Variance Of Normal \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). Consider a distribution with mean $\mu$, variance $\sigma^2$, skewness $\gamma$ and kurtosis $\kappa$ (where all these moments are finite). Theorem 7.2.3 states that the distribution of the sample variance, when sampling from a normally distributed. If an arbitrarily large number of. Distribution Of Sample Variance Of Normal.
From www.slideserve.com
PPT Continuous distributions PowerPoint Presentation, free download Distribution Of Sample Variance Of Normal If an arbitrarily large number of samples, each involving multiple observations (data points), were separately used in order to compute one value. Assuming $n$ samples $\{x_1,.,x_n\}$ are taken from a normal distribution with mean $\mu$ and variance $\sigma^2$, then the variance can be. \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution. Distribution Of Sample Variance Of Normal.
From www.slideserve.com
PPT Variance Formula PowerPoint Presentation, free download ID7084253 Distribution Of Sample Variance Of Normal If an arbitrarily large number of samples, each involving multiple observations (data points), were separately used in order to compute one value. Consider a distribution with mean $\mu$, variance $\sigma^2$, skewness $\gamma$ and kurtosis $\kappa$ (where all these moments are finite). Theorem 7.2.3 states that the distribution of the sample variance, when sampling from a normally distributed. \(x_1, x_2, \ldots,. Distribution Of Sample Variance Of Normal.
From www.teachoo.com
Example 12 Calculate mean, variance, standard deviation Distribution Of Sample Variance Of Normal Consider a distribution with mean $\mu$, variance $\sigma^2$, skewness $\gamma$ and kurtosis $\kappa$ (where all these moments are finite). Theorem 7.2.3 states that the distribution of the sample variance, when sampling from a normally distributed. \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). Assuming $n$ samples $\{x_1,.,x_n\}$ are taken. Distribution Of Sample Variance Of Normal.
From www.qualitygurus.com
One Sample Variance Test (Chisquare) Quality Gurus Distribution Of Sample Variance Of Normal Theorem 7.2.3 states that the distribution of the sample variance, when sampling from a normally distributed. Assuming $n$ samples $\{x_1,.,x_n\}$ are taken from a normal distribution with mean $\mu$ and variance $\sigma^2$, then the variance can be. \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). If an arbitrarily large. Distribution Of Sample Variance Of Normal.
From www.freecodecamp.org
689599 Rule Normal Distribution Explained in Plain English Distribution Of Sample Variance Of Normal \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). Consider a distribution with mean $\mu$, variance $\sigma^2$, skewness $\gamma$ and kurtosis $\kappa$ (where all these moments are finite). Theorem 7.2.3 states. Distribution Of Sample Variance Of Normal.
From bookdown.org
11 Two Sample Inferential Statistics PSY317L & PSY120R Guidebook Distribution Of Sample Variance Of Normal \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). Assuming $n$ samples $\{x_1,.,x_n\}$ are taken from a normal distribution with mean $\mu$ and variance $\sigma^2$, then the variance can be. Consider a distribution with mean $\mu$, variance $\sigma^2$, skewness $\gamma$ and kurtosis $\kappa$ (where all these moments are finite). If. Distribution Of Sample Variance Of Normal.
From www.scribbr.com
Normal Distribution Examples, Formulas, & Uses Distribution Of Sample Variance Of Normal \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). Assuming $n$ samples $\{x_1,.,x_n\}$ are taken from a normal distribution with mean $\mu$ and variance $\sigma^2$, then the variance can be. Consider a distribution with mean $\mu$, variance $\sigma^2$, skewness $\gamma$ and kurtosis $\kappa$ (where all these moments are finite). If. Distribution Of Sample Variance Of Normal.
From www.scribbr.com
Normal Distribution Examples, Formulas, & Uses Distribution Of Sample Variance Of Normal \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). If an arbitrarily large number of samples, each involving multiple observations (data points), were separately used in order to compute one value. Theorem 7.2.3 states that the distribution of the sample variance, when sampling from a normally distributed. \(x_1, x_2, \ldots,. Distribution Of Sample Variance Of Normal.
From mrs-mathpedia.com
The Variance and Standard Deviation Mrs.Mathpedia Distribution Of Sample Variance Of Normal Theorem 7.2.3 states that the distribution of the sample variance, when sampling from a normally distributed. Consider a distribution with mean $\mu$, variance $\sigma^2$, skewness $\gamma$ and kurtosis $\kappa$ (where all these moments are finite). Assuming $n$ samples $\{x_1,.,x_n\}$ are taken from a normal distribution with mean $\mu$ and variance $\sigma^2$, then the variance can be. \(x_1, x_2, \ldots, x_n\). Distribution Of Sample Variance Of Normal.
From www.scribbr.com
Normal Distribution Examples, Formulas, & Uses Distribution Of Sample Variance Of Normal If an arbitrarily large number of samples, each involving multiple observations (data points), were separately used in order to compute one value. Assuming $n$ samples $\{x_1,.,x_n\}$ are taken from a normal distribution with mean $\mu$ and variance $\sigma^2$, then the variance can be. \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution. Distribution Of Sample Variance Of Normal.
From www.youtube.com
Sampling distributions for the mean proportion and variance YouTube Distribution Of Sample Variance Of Normal If an arbitrarily large number of samples, each involving multiple observations (data points), were separately used in order to compute one value. Consider a distribution with mean $\mu$, variance $\sigma^2$, skewness $\gamma$ and kurtosis $\kappa$ (where all these moments are finite). \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\).. Distribution Of Sample Variance Of Normal.
From faculty.nps.edu
Chapter 9 Introduction to Sampling Distributions Introduction to Distribution Of Sample Variance Of Normal Assuming $n$ samples $\{x_1,.,x_n\}$ are taken from a normal distribution with mean $\mu$ and variance $\sigma^2$, then the variance can be. If an arbitrarily large number of samples, each involving multiple observations (data points), were separately used in order to compute one value. Consider a distribution with mean $\mu$, variance $\sigma^2$, skewness $\gamma$ and kurtosis $\kappa$ (where all these moments. Distribution Of Sample Variance Of Normal.
From sixsigmadsi.com
Population Variance Sixsigma DSI Lean Six Sigma Glossary Term Distribution Of Sample Variance Of Normal Consider a distribution with mean $\mu$, variance $\sigma^2$, skewness $\gamma$ and kurtosis $\kappa$ (where all these moments are finite). If an arbitrarily large number of samples, each involving multiple observations (data points), were separately used in order to compute one value. \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\).. Distribution Of Sample Variance Of Normal.
From www.youtube.com
Sample & Population Variance & Standard Deviation YouTube Distribution Of Sample Variance Of Normal \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). Theorem 7.2.3 states that the distribution of the sample variance, when sampling from a normally distributed. \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). Assuming $n$ samples $\{x_1,.,x_n\}$ are taken. Distribution Of Sample Variance Of Normal.
From www.scribbr.com
The Standard Normal Distribution Examples, Explanations, Uses Distribution Of Sample Variance Of Normal Theorem 7.2.3 states that the distribution of the sample variance, when sampling from a normally distributed. \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). Assuming $n$ samples $\{x_1,.,x_n\}$ are taken from a normal distribution with mean $\mu$ and variance $\sigma^2$, then the variance can be. Consider a distribution with. Distribution Of Sample Variance Of Normal.
From www.knowhowadda.com
How to Calculate Variance knowhowadda Distribution Of Sample Variance Of Normal Assuming $n$ samples $\{x_1,.,x_n\}$ are taken from a normal distribution with mean $\mu$ and variance $\sigma^2$, then the variance can be. Theorem 7.2.3 states that the distribution of the sample variance, when sampling from a normally distributed. If an arbitrarily large number of samples, each involving multiple observations (data points), were separately used in order to compute one value. \(x_1,. Distribution Of Sample Variance Of Normal.
From slideplayer.com
Data Mining 2018/2019 Fall MIS 331 Chapter 7A Sampliing Distribution Distribution Of Sample Variance Of Normal \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\). If an arbitrarily large number of samples, each involving multiple observations (data points), were separately used in order to compute one value. Assuming $n$ samples $\{x_1,.,x_n\}$ are taken from a normal distribution with mean $\mu$ and variance $\sigma^2$, then the variance. Distribution Of Sample Variance Of Normal.